[考试记录] 2024.7.15 csp-s模拟赛4

2024.7.15 csp-s模拟赛4

T1 传送带

题面翻译

有一个长度为 \(n\) 的一维网格。网格的第 \(i\) 个单元格包含字符 \(s_i\) ，是“<”或“>”。当弹球放在其中一个格子上时，它会按照以下规则移动：

如果弹球位于第 \(i\) 个格子上且 \(s_i\) 为 '<'，则弹球在下一秒会向左移动一个单元格；如果 \(s_i\) 为 '>'，则向右移动一个单元格。弹球移动后，字符 \(s_i\) 会反转（即，如果 \(s_i\) 原来是 '<'，则变为 '>'，反之亦然）。无论是离开左边界还是从右边界,当弹球离开网格时，它都会停止移动。

您需要回答 \(t（1\le t \le 10^5）\) 个独立的查询。每一组查询中有一个长度 \(n（1\le n\le 5\times10^5）\)，及一个只包含 “<” 和 “>”的字符串。弹球可以放在任意一个位置上。对于每个查询，在同一行输出 \(n\) 个数，第 \(i\) 个数表示弹球放置在第 \(i\) 格时离开网格的时长，用空格隔开。

题目描述

There is a one-dimensional grid of length $ n $ . The $ i $ -th cell of the grid contains a character $ s_i $ , which is either '<' or '>'.

When a pinball is placed on one of the cells, it moves according to the following rules:

• If the pinball is on the $ i $ -th cell and $ s_i $ is '<', the pinball moves one cell to the left in the next second. If $ s_i $ is '>', it moves one cell to the right.
• After the pinball has moved, the character $ s_i $ is inverted (i. e. if $ s_i $ used to be '<', it becomes '>', and vice versa).
• The pinball stops moving when it leaves the grid: either from the left border or from the right one.

You need to answer $ n $ independent queries. In the $ i $ -th query, a pinball will be placed on the $ i $ -th cell. Note that we always place a pinball on the initial grid.

For each query, calculate how many seconds it takes the pinball to leave the grid. It can be shown that the pinball will always leave the grid within a finite number of steps.

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^5 $ ). The description of the test cases follows.

The first line of each test case contains an integer $ n $ ( $ 1 \le n \le 5 \cdot 10^5 $ ).

The second line of each test case contains a string $ s_1s_2 \ldots s_{n} $ of length $ n $ consisting of characters '<' and '>'.

It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 5 \cdot 10^5 $ .

输出格式

For each test case, for each $ i $ ( $ 1 \le i \le n $ ) output the answer if a pinball is initially placed on the $ i $ -th cell.

样例 #1

样例输入 #1

3
3
><<
4
<<<<
6
<><<<>

样例输出 #1

3 6 5
1 2 3 4
1 4 7 10 8 1

提示

In the first test case, the movement of the pinball for $ i=1 $ is shown in the following pictures. It takes the pinball $ 3 $ seconds to leave the grid.

The movement of the pinball for $ i=2 $ is shown in the following pictures. It takes the pinball $ 6 $ seconds to leave the grid.

解析

部分分

60pts

可以发现对于每个 \(i\) 开始移动的下标，他会沿着 \(i\) 开始的方向来回弹跳直到走出去，且幅度越来越大。所以很容易想到，对每个点跑双指针模拟这个过程，扩展的过程就是暴力跳下标，理论时间复杂度 \(\mathcal{O}(N^2)\)，但实际复杂度可能到 \(\mathcal{O}(N^3)\) 甚至到 \(\mathcal{O}(N^4)\)，比如大于小于号交替的极限数据。

#include<bits/stdc++.h>
using namespace std;
int n; string s;
int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>s;
	for(int i=1; i<=n; ++i){
		string k = s;
		int ans = 0, it = i;
		while(it && it <= n){
			if(k[it-1] == '<') k[--it] = '>';
			else k[it-1] = '<', ++it;
			++ans;
		}
		cout<<ans<<' ';
	} return 0;
}

80pts

60pts 的优化版。我们不去一个一个跳下标，而是预处理出下一个和上一个大于小于号的位置，直接转移。由此对每个点用双指针模拟这个过程即可。

#include<bits/stdc++.h>
using namespace std;
#define int long long
constexpr int N = 5e5 + 5;
int n, nxt[N], lst[N], dayu, xiaoyu;
string s;
signed main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>s;
	xiaoyu = n+1, dayu = n+1;
	for(int i=n; i>=1; --i){
		if(s[i-1] == '>'){
			nxt[i] = xiaoyu;
			dayu = i;
		}
		else{
			nxt[i] = xiaoyu;
			xiaoyu = i;
		}
	}
	dayu = 0, xiaoyu = 0;
	for(int i=1; i<=n; ++i){
		if(s[i-1] == '<'){
			lst[i] = dayu;
			xiaoyu = i;
		} else{
			lst[i] = dayu;
			dayu = i;
		}
	}
	for(int i=1; i<=n; ++i){
		int l = i, r = i, ans = 0;
		if(s[i-1] == '<'){
			while(l && r <= n){
				l = lst[l], ans += r - l;
				if(!l) break;
				r = nxt[r], ans += r - l;
			}
		}
		else{
			while(l && r <= n){
				r = nxt[r], ans += r - l;
				if(r > n) break;
				l = lst[l], ans += r - l;
			}
		}
		cout<<ans<<' ';
	}
	return 0;
}

正解

两个方法复杂度都为 \(\mathcal{O}(N)\)，法二常数小。

法一

观察来回弹跳时对答案产生的贡献，比如 \(i\) 在 < 开始，向左跳到第一个 >，然后变向，向右跳到 \(i\) 右边第一个 <，以此类推。所以最后的答案就是：

\[\begin{split}
ans_i&=(i-l_1)+(r_1-l_1)+(r_1-l_2)+\cdots +(r_{k-1}-l_{k-1})+r_k\\
&=i+2*\sum r_k-l_k
\end{split}
\]

维护 \(l\) 和 \(r\) 的前缀和，讨论起始方向计算即可。

法二

考虑相邻答案的转移。考虑串 ><>><，第一个 > 走到右边第一个 < 时变向，所以第一个 > 对答案产生的贡献为 \(2\times (r-i)-1\)。\(r\) 为第一个 < 的坐标。接着看下一个字符 <，可以看作第一个字符 > 向右走到 < 然后回到 >，由于贡献是累加起来的，所以 \(sum+=2\times (r-i)-1\)。然后把 \(sum\) 贡献到答案里去。

由于当前只考虑了向右跳过去跳回来的贡献，所以还要跑一遍向左跳过去跳回来的情况。

#include<bits/stdc++.h>
using namespace std;
#define int long long
constexpr int N = 5e5 + 5;
string s;  int n, ans[N];
signed main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>s;
	for(int i=1, j=1, sum=0; i<=n; ++i){
		while(j <= n && s[j-1] == '>') ++j;
		if(j > n) break;
		sum += 2 * (j++ - i) + 1;
		ans[i] += sum;
	}
	for(int i=n, j=n, sum=0; i>=1; --i){
		while(j >= 1 && s[j-1] == '<') --j;
		if(j < 1) break;
		sum += 2 * (i - j--) + 1;
		ans[i] += sum;
	}
	for(int i=1; i<=n; ++i) cout<<ans[i]<<' ';
	return 0;
}

T2 math

Description

沉迷于数学的小G最近口胡出一种数据生成方法： 开始，小G有一个长度为 \(n\) 的正整数序列，序列中的第 \(i\) 个数为 \(a_i\in [1,10^9]\)。 然后，小G会通过某种方式生成一个长度为 \(n\) 的非负整数序列，序列中的第 \(i\) 个数为 \(b_i\in[0,+\infty]\)。 最终，小G会得到一个整数 \(x=\sum\limits_{i=1}^{n}a_ib_i\bmod k\)。

小G想知道这种数据生成方法可以生成哪些不同的非负整数。

Sample

样例输入

2 8
4 12

样例输出

2
0 4

解析

很好的数论题，但考场上并没有推出这一结论，而是找归路分类讨论，wa了几个点，78pts。

很好的数论题。考虑 \(n=1\) 的情况，有 \(a*b \equiv x \pmod{k}\)，可化为 \(ab+ky=x\)。若该狮子有整数解，那么当且仅当 \(\gcd(a,k)\mid x\)。因此答案 \(x\) 只能是 \(gcd\) 的整数倍，并且小于 \(k\)。所以计算出所有 \(a\) 与 \(k\) 的 \(gcd\)，枚举输出答案即可。复杂度 \(\mathcal{O}((n+v)\log n)\)。

#include<bits/stdc++.h>
using namespace std;
int n, k, gcd, a, ans;
int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>k; gcd = k;
	for(int i=1; i<=n; ++i) cin>>a, gcd = __gcd(a, gcd);
	ans = k / gcd; cout<<ans<<'\n';
	for(int i=0; i*gcd < k; ++i) cout<<i*gcd<<' ';
	return  0;
}

T3

letax 懒得打了。

解析

很好的DP题。暴力40pts。

首先对每个 \(a!=0\) 的点进行排序，这是显然的。然后我就在思考怎么单调队列 \(\mathcal{O}(n)\) 转移，然后发现这个绝对值把 i 和 j 绑在一起了，然后就想怎么把绝对值去掉，然后就考虑平方一下，然后成功地又把 i 和 j 绑一起了。于是打BL。其实单调队列也可以维护，只不过要把坐标转为切比雪夫距离，最后记录路径计算答案即可。

不会切比雪夫）：？考虑简单DP。设当前需要转移的点为 \(i\) ，那么 \(j\) 可以在 \(i\) 的左上、左下、右上和右下四种情况。需要在转移时判断点在那个方位吗？不需要，因为取绝对值的原因，所以 xy 坐标给的贡献必须大于 0，所以只要在这四种转移里取 max 即可。这是本题极为关键的一点。

#include<bits/stdc++.h>
using namespace std;
#define int long long
constexpr int N = 2e3 + 2;
int n, m, x[N*N], y[N*N], a[N*N], b[N*N], cnt, dp[N*N], p1[N*N], num2[N*N], tot;
int rnk[N][N], srt[N*N], p[N*N], num[N*N], tail, way[N*N], ans, nxt[4], lst[4];
bool cmp(int q, int w){ return a[q] < a[w]; }
int dx[4] = {1, 1, -1, -1}, dy[4] = {1, -1, 1, -1};
signed main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>m;
	for(int i=1; i<=n; ++i) for(int j=1; j<=m; ++j){
		cin>>a[++cnt];
		x[cnt] = i, y[cnt] = j;
		rnk[i][j] = cnt;
		srt[cnt] = cnt;
	}
	for(int i=1; i<=n; ++i) for(int j=1; j<=m; ++j)
		cin>>b[rnk[i][j]];
	sort(srt+1, srt+1+cnt, cmp);
	int bg = 1; while(!a[srt[bg]]) ++bg;
	for(int i=bg; i<=cnt; ++i){
		if(a[srt[i]] != a[srt[i-1]] && a[srt[i-1]]){ bg = i; break; }
		dp[srt[i]] = b[srt[i]];
		for(int j=0; j<4; ++j)
			nxt[j] = max(nxt[j], dp[srt[i]] + x[srt[i]]*dx[j] + y[srt[i]]*dy[j]);
		ans = max(ans, dp[srt[i]]);
	}
	for(int i=bg; i<=cnt; ++i){
		if(a[srt[i]] != a[srt[i-1]]) for(int j=0; j<4; ++j)
			lst[j] = nxt[j], nxt[j] = 0;
		for(int j=0; j<4; ++j)
			dp[srt[i]] = max(dp[srt[i]], b[srt[i]] - x[srt[i]]*dx[j] - y[srt[i]]*dy[j] + lst[j]);
		for(int j=0; j<4; ++j)
			nxt[j] = max(nxt[j], dp[srt[i]] + x[srt[i]]*dx[j] + y[srt[i]]*dy[j]);
		ans = max(ans, dp[srt[i]]);
	}
	return cout<<ans, 0;
}

T4

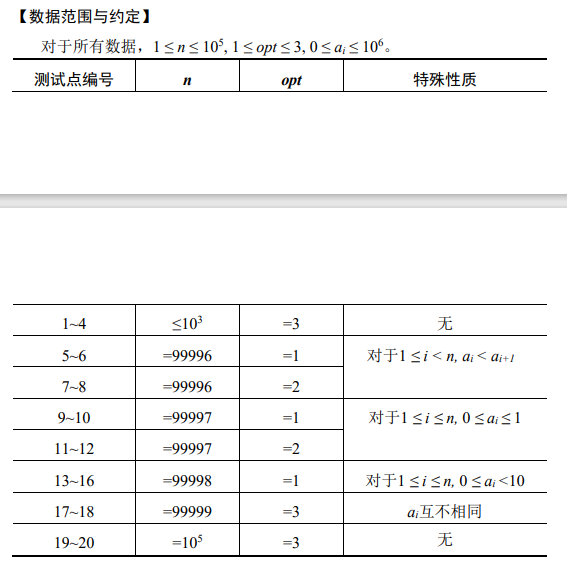
个人能力有限，暂时该不出来，所以先咕~。