Competition Set - 2023杭电多校
关于代码太多导致太卡然后发现刚好可以放下HDU多校这回事。
那就稍微加点经历吧。team316。
第十场
今天发挥还行。
上来开03,一发过。然后做09,感觉就不难,过之。发现11是数学题,干,想了2小时过了。剩下的时间在调计算几何,调不过去。
队友也给力,7道题排名29。
1009 Far Away from Home
一条数轴上有 \(n\) 个商店,每个商店售卖一些物品,总共 \(m\) 种。在数轴上选择一个位置作为家,然后从家出门 \(m\) 次,每次买一种商品。最小化走的距离。
\(n\le 10^5,m\le 5\cdot 10^5\)。
Solution:显然只用考虑家和某个商店重合的情况,所以先离散化,然后扫描每种物品,二分找到每个商店覆盖的区间,就要进行区间加一次函数。两个差分维护即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+5;
int T,n,c,x[N];ll s[N],t[N],ans;
vector<int> a[N];
inline void add(int l,int r,int x,int y){
s[l]+=y;s[r+1]-=y;t[l]+=x;t[r+1]-=x;
}
int main(){
ios::sync_with_stdio(false);
cin>>T;
while(T--){
cin>>n>>c;ans=1e18;
for(int i=1,k;i<=n;i++){
cin>>x[i]>>k;
for(int j=1,y;j<=k;j++){
cin>>y;
a[y].push_back(x[i]);
}
}
sort(x+1,x+n+1);n=unique(x+1,x+n+1)-x-1;
for(int i=1;i<=c;i++){
sort(a[i].begin(),a[i].end());
add(1,lower_bound(x+1,x+n+1,a[i][0])-x,a[i][0],-1);
int len=a[i].size();
for(int j=1;j<len;j++){
int p=a[i][j-1],q=a[i][j];
int p1=lower_bound(x+1,x+n+1,p)-x,
q1=lower_bound(x+1,x+n+1,q)-x;
int L=p1+1,R=q1,pos=q1;
while(L<=R){
int mid=L+R>>1;
if(x[mid]-p<q-x[mid])L=mid+1;
else pos=mid,R=mid-1;
}
add(p1+1,pos-1,-p,1);add(pos,q1,q,-1);
}
add(lower_bound(x+1,x+n+1,a[i][len-1])-x+1,n,-a[i][len-1],1);
a[i].clear();
}
for(int i=1;i<=n;i++){
s[i]+=s[i-1],t[i]+=t[i-1];
ans=min(ans,t[i]+s[i]*x[i]);
}
cout<<ans<<endl;
for(int i=0;i<=n+1;i++)s[i]=t[i]=0;
}
return 0;
}
1011 Werewolves
\(n\) 个人,主持人给每个人 \(m\) 个身份中的一种,但不让它们知道。接下来主持人告诉每个人另外 \(n-1\) 个人的身份构成的可重集。构造一种方案,给每个人遇到每个可重集规定一个回答(不受其他人回答影响),使得总能够有 \(\lfloor \frac{n}{m} \rfloor\) 个人猜对。
Solution:第 \(i\) 个人假设所有人的身份之和模 \(m\) 同余于 \(i\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int T,n,m,k,s[2100005];
void dfs(int p,int lst,int sum){
if(p==n){
s[++k]=sum;
return;
}
for(int i=lst;i<=m;i++)
dfs(p+1,i,(sum+i)%m);
}
int main(){
ios::sync_with_stdio(false);
cin>>T;
while(T--){
cin>>n>>m;
k=0;dfs(1,1,0);
for(int i=1;i<=n;i++){
for(int j=1;j<=k;j++)
cout<<(i%m-s[j]+m)%m+1<<' ';
cout<<endl;
}
}
return 0;
}
第九场
又是平平无奇的一天。
开场看02,试图找规律,找不出来。队友说写一个搜索试试,我不太赞同,但是他写了,但是他过了。然后我成小丑了。看12,发现是shaber题,写之,过之。看了04,看了07,都不怎么会。本来给队友的11拿来做,NTT,TLE。一直在WA和TLE,最后就结束了。
然后发现是没清空?淦。
1002 Shortest path
已知从 \(i\) 开始可以一步走到 \(2i,3i,i+1\),问从 \(1\) 走到 \(n\) 需要多少步。\(T\) 次询问。
\(t \le 2000,n\le 10^{18}\)。
Solution:倒序操作,进行记忆化搜索即可。注意不会两次减一后除以二,或者三次减一后除以三,所以只用从 \(n\) 搜到 \(\lfloor \frac{n}{2} \rfloor,\lfloor \frac{n}{3} \rfloor\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int T;ll n;
map<ll,int> M;
int dfs(ll x){
if(x<=1)return 0;if(M[x])return M[x];
return M[x]=min(dfs(x/2)+x%2+1,dfs(x/3)+x%3+1);
}
int main(){
ios::sync_with_stdio(false);
cin>>T;
while(T--){
cin>>n;
cout<<dfs(n)<<'\n';
}
return 0;
}
1004 Broken Dream
\(n\) 个点,\(m\) 条边的图,每条边有一个长度,一个可用概率。问所有可用的边和所有点构成的子图的最小生成树的边的长度和的期望。如果没有最小生成树,认为长度和为 \(0\)。
\(n\le 15,m\le 50\)。
Solution:一眼状压DP,设 \(g_{i,S}\) 表示前 \(i\) 条边在集合 \(S\) 内的 MST 的期望。然后发现递推还需要概率,但不能直接拿总的概率,所以设计\(f_{i,S}\) 表示前 \(i\) 条边中在集合 \(S\) 内的边连通 \(S\) 的概率。对于第 \(i\) 条边 \((u,v,w)\) 和集合 \(S\),由 \(S\) 的子集 \(L,R\) 转移而来,要求 \(u \in L,v\in R,L \cap R = \emptyset,L\cup R=S\)。转移方程为
\]
\]
这里的 \(p\) 是第 \(i\) 条边被选中的概率,这就要求前 \(i-1\) 条边不连通 \(L,R\)。我们再设 \(h_{i,S}\) 表示前 \(i\) 条边连通集合 \(S\) 的概率,则 \(p=\frac{h_S}{h_Lh_R}\)。对 \(u,v\in S\),\(h_{i,S}\) 等于 \(h_{i-1,S}\) 乘以第 \(i\) 条边可用的概率。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int P=998244353;
int T,n,m,f[55][1<<15],g[55][1<<15],h[1<<15],ih[1<<15];
struct edge{int u,v,w,p;}e[55];
bool operator <(const edge&a,const edge&b){return a.w<b.w;}
int qpow(int a,int b){int c=1;for(;b;b>>=1,a=1ll*a*a%P)if(b&1)c=1ll*c*a%P;return c;}
int main(){
ios::sync_with_stdio(false);
cin>>T;
while(T--){
memset(f,0,sizeof(f));memset(g,0,sizeof(g));
cin>>n>>m;
for(int i=1;i<=m;i++)
cin>>e[i].u>>e[i].v>>e[i].w>>e[i].p;
sort(e+1,e+m+1);
for(int i=0;i<n;i++)f[0][1<<i]=1;
for(int i=0;i<(1<<n);i++)h[i]=ih[i]=1;
for(int i=1;i<=m;i++){
int u=e[i].u-1,v=e[i].v-1,invp=qpow(P+1-e[i].p,P-2);
for(int s=0;s<(1<<n);s++){
f[i][s]=f[i-1][s];g[i][s]=g[i-1][s];
if(!(s&(1<<u))||!(s&(1<<v)))continue;
for(int L=s;L;L=s&(L-1)){
if(!(L&(1<<u))||(L&(1<<v)))continue;
int R=s^L,p=1ll*h[s]*ih[L]%P*ih[R]%P*e[i].p%P;
f[i][s]=(f[i][s]+1ll*f[i-1][L]*f[i-1][R]%P*p%P)%P;
g[i][s]=(g[i][s]+(1ll*g[i-1][L]*f[i-1][R]%P+1ll*f[i-1][L]*g[i-1][R]%P+
1ll*f[i-1][L]*f[i-1][R]%P*e[i].w%P)*p%P)%P;
}
h[s]=1ll*h[s]*(P+1-e[i].p)%P;ih[s]=1ll*ih[s]*invp%P;
}
}
cout<<g[m][(1<<n)-1]<<endl;
}
return 0;
}
1007 Average
给定一棵 \(n\) 个点的树,点有权,求长度大于 \(k\) 的路径中点权平均数最大值。有 \(q\) 次单点增加。
\(n\le 10^5,q\le10^4,k\le30\)。
Solution:一眼点分治,但看到平均数又只好二分,然后发现没法做。注意到 \(k\) 很小,思考后发现性质:答案路径的长度一定不超过 \(2k-1\),否则可以拆成两段长度不小于 \(k\) 的路径,取较大的一个不劣。然后就可考虑处理出以 \(u\) 为起点,向子树内深度为 \(d\le 2k\) 的路径点权和的最大值和次大值(要求不在一个子树内),在每个点上 \(O(k^2)\) 处理答案即可。询问时只要更新 \(2k\) 级祖先,时间复杂度 \(O(nk^2+qk^3)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
const ll INF=1ll<<60;
struct frac{ll x,y;}ans;
bool operator <(const frac&a,const frac&b){return a.x*b.y<a.y*b.x;}
void chkmax(frac&a,frac b){if(a<b)a=b;}
void print(frac a){ll d=__gcd(a.x,a.y);cout<<a.x/d<<"/"<<a.y/d<<endl;}
int T,n,k,fa[N],q,fp[N][65],gp[N][65];ll a[N],f[N][65],g[N][65];
vector<int> G[N];
void dfs(int u){
f[u][0]=g[u][0]=a[u];fp[u][0]=gp[u][0]=u;
for(int v:G[u])if(v!=fa[u]){
fa[v]=u;dfs(v);
for(int d=1;d<=2*k;d++)if(fp[v][d-1]){
if(a[u]+f[v][d-1]>f[u][d]){
g[u][d]=f[u][d],f[u][d]=a[u]+f[v][d-1];
gp[u][d]=fp[u][d],fp[u][d]=v;
}
else if(a[u]+f[v][d-1]>g[u][d])
g[u][d]=a[u]+f[v][d-1],gp[u][d]=v;
}
}
for(int i=0;i<=2*k;i++)
for(int j=max(k-1-i,0);j<=2*k-i;j++){
if(fp[u][i]&&fp[u][j]&&fp[u][i]!=fp[u][j])
chkmax(ans,{f[u][i]+f[u][j]-a[u],i+j+1});
else{
if(fp[u][i]&&gp[u][j])chkmax(ans,{f[u][i]+g[u][j]-a[u],i+j+1});
if(fp[u][j]&&gp[u][i])chkmax(ans,{f[u][j]+g[u][i]-a[u],i+j+1});
}
}
}
int main(){
ios::sync_with_stdio(false);
cin>>T;
while(T--){
ans={0,1};
for(int i=1;i<=n;i++){
G[i].clear();fa[i]=0;
for(int j=0;j<=2*k;j++)
f[i][j]=g[i][j]=fp[i][j]=gp[i][j]=0;
}
cin>>n>>k;
for(int i=1,x;i<=n;i++)cin>>x,a[i]=x;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs(1);
cin>>q;
for(int i=1,u,x;i<=q;i++){
cin>>u>>x;a[u]+=x;
for(int d=0;d<=2*k;d++){if(fp[u][d])f[u][d]+=x;if(gp[u][d])g[u][d]+=x;}
for(int t=0;t<=2*k;t++)
for(int j=max(k-1-t,0);j<=2*k-t;j++){
if(fp[u][t]&&fp[u][j]&&fp[u][t]!=fp[u][j])
chkmax(ans,{f[u][t]+f[u][j]-a[u],t+j+1});
else{
if(fp[u][t]&&gp[u][j])chkmax(ans,{f[u][t]+g[u][j]-a[u],t+j+1});
if(fp[u][j]&&gp[u][t])chkmax(ans,{f[u][j]+g[u][t]-a[u],t+j+1});
}
}
int v=u;
for(int j=1;j<=2*k&&v!=1;j++,v=fa[v]){
u=fa[v];
for(int d=1;d<=2*k;d++)if(fp[v][d-1]){
if(a[u]+f[v][d-1]>f[u][d]){
if(v==fp[u][d])f[u][d]=a[u]+f[v][d-1];
else g[u][d]=f[u][d],f[u][d]=a[u]+f[v][d-1],
gp[u][d]=fp[u][d],fp[u][d]=v;
}
else if(a[u]+f[v][d-1]>g[u][d]&&fp[u][d]!=v)
g[u][d]=a[u]+f[v][d-1],gp[u][d]=v;
}
for(int t=0;t<=2*k;t++)
for(int j=max(k-1-t,0);j<=2*k-t;j++){
if(fp[u][t]&&fp[u][j]&&fp[u][t]!=fp[u][j])
chkmax(ans,{f[u][t]+f[u][j]-a[u],t+j+1});
else{
if(fp[u][t]&&gp[u][j])chkmax(ans,{f[u][t]+g[u][j]-a[u],t+j+1});
if(fp[u][j]&&gp[u][t])chkmax(ans,{f[u][j]+g[u][t]-a[u],t+j+1});
}
}
}
print(ans);
}
}
return 0;
}
1011 Cargo
\(n\) 个商店,出售的物品有 \(m\) 种。一人 \(k\) 次等概率选取一家商店买其物品。求:不存在一种物品,此人在出售它的每家商店恰好买了一次。
\(m\le n\le 2\cdot 10^5,k\lt 998244353\).
Solution:考虑容斥,假设第 \(i\) 种物品有 \(c_i\) 个,不合法的物品集合(至少)为 \(I\)。则这样的方案数为
\]
前面是选择买 \(I\) 中物品的位置,后面是剩下的位置的购买。
注意到这个式子只跟 \(\sum_{i\in I}c_i\) 有关,所以只要对 \(c_i\) 做一个多重背包即可。\(c_i\) 的和为 \(n\),所以不同 \(c_i\) 的个数不超过 \(\sqrt n\),于是转化为多重背包问题。用 NTT 转移即可。加上火车头在HDU可过。
点击查看代码
#include<bits/stdc++.h>
#define clr(f,n) memset(f,0,sizeof(int)*(n))
#define cpy(f,g,n) memcpy(f,g,sizeof(int)*(n))
#define RE register
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=3e5+5,P=998244353,_G=3;
ll qpow(ll a,ll b){ll c=1;for(;b;b>>=1,a=a*a%P)if(b&1)c=c*a%P;return c;}
const int invG=qpow(_G,P-2);
int tr[N<<1],tf;ll sav[N<<1];ull f[N<<1],w[N<<1];
void tpre(int n){
if(tf==n)return;tf=n;
for(int i=0;i<n;i++)
tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
}
void NTT(ll *g,bool op,int n){
tpre(n);
memset(f,0,sizeof(f));
memset(w,0,sizeof(w));w[0]=1;
for(int i=0;i<n;i++)f[i]=(g[tr[i]]%P+P)%P;
for(int l=1;l<n;l<<=1){
ull tG=qpow(op?_G:invG,(P-1)/(l+l));
for(int i=1;i<l;i++)w[i]=w[i-1]*tG%P;
for(int k=0;k<n;k+=l+l)
for(int p=0;p<l;p++){
int tt=w[p]*f[k|l|p]%P;
f[k|l|p]=f[k|p]+P-tt;
f[k|p]+=tt;
}
for(int i=0;i<n;i++)f[i]%=P;
}
if(!op){
ull invn=qpow(n,P-2);
for(int i=0;i<n;++i)g[i]=f[i]*invn%P;
}
else for(int i=0;i<n;++i)g[i]=f[i]%P;
}
void px(ll *f,ll *g,int n){for(int i=0;i<n;++i)f[i]=f[i]*g[i]%P;}
void times(ll *f,ll *g,int len){
int n=1;for(n;n<len+len;n<<=1);
memset(sav,0,sizeof(sav));cpy(sav,g,n);
NTT(f,1,n);NTT(sav,1,n);px(f,sav,n);NTT(f,0,n);
}
int T,m,n,k,b[N],c[N];ll dp[N<<1],g[N],ans,fac[N],facinv[N];
ll C(int n,int m){return fac[n]*facinv[n-m]%P*facinv[m]%P;}
int main(){
ios::sync_with_stdio(false);
fac[0]=facinv[0]=1;
for(RE int i=1;i<N;++i)facinv[i]=qpow(fac[i]=fac[i-1]*i%P,P-2);
cin>>T;
while(T--){
cin>>n>>m>>k;dp[0]=1;
for(RE int i=1,x;i<=n;++i){cin>>x;++c[x];}
for(RE int i=1;i<=m;++i)++b[c[i]];
for(RE int i=1;i<=n;++i)if(b[i]){
for(RE int j=0;j<=b[i];++j)
g[i*j]=(j&1)?P-C(b[i],j):C(b[i],j);
times(dp,g,n+1);
for(RE int j=0;j<=b[i];++j)g[i*j]=0;
}
for(RE int i=0,fac=1;i<=min(n,k);++i){
ans=(ans+dp[i]*qpow(n-i,k-i)%P*fac%P)%P;
fac=1ll*fac*(k-i)%P;
}
cout<<ans*qpow(qpow(n,k),P-2)%P<<endl;
ans=0;for(int i=1;i<=m;++i)c[i]=0;
for(int i=0;i<=n;++i)b[i]=dp[i]=dp[i+n]=0;dp[0]=1;
}
return 0;
}
第八场
今天纯战犯。
上来签了07,然后开始看06。看了一会会了一个 \(O(n\log n)\) 的 KMP+树状数组做法,然后不知道怎么想的觉得能过,开写,T。然后想了一会哈希,会了一个做法,先后用sort,map,unordered_map实现,都寄。大概3点半上网搜手写哈希表过了。后面什么都没干。
不过队友比较给力,7道题排名43.
1006 Nested String
给定字符串 \(T1,T2,S\),求 \(S\) 有多少个子串可以由 \(T2\) 插入 \(T1\) 得到。注意不同的插入位置算不同的方案。
\(|S| \le 10^7\)。
Solution:字符串哈希,先求出将 \(T2\) 插入 \(T1\) 得到的所有串的哈希值并记录个数,然后扫描 \(S\) 统计答案。
#pragma GCC optimize(3)
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<ctime>
#define RE register
using namespace std;
typedef unsigned long long ull;
struct my_hash{
static const int BUFF=8388607;
static const int EDGE=10000010;
int fi[BUFF+1],k,ne[EDGE];//wei chu shi hua
ull b[EDGE];
int c[EDGE];
__attribute__((always_inline)) int& operator [](const ull &x){
int temp=x&BUFF;
if (fi[temp]){
for (int j=fi[temp]; j; j=ne[j])
if (b[j]==x) return c[j];
ne[++k]=fi[temp];
b[fi[temp]=k]=x;
return c[k];
}
ne[++k]=0;
b[fi[temp]=k]=x;
return c[k];
}
void clear(){
for (int i=1; i<=k; ++i) c[i]=int();
k=0;
memset(fi,0,(BUFF+1)*sizeof(*fi));
}
}H;
const int N=1.1e7+5;
int T,n,m1,m2;char s[N],t1[N],t2[N];long long ans;
ull p[N],h0,h1[N],h2[N],base=131;
int main(){
// double T1=clock()*1000/CLOCKS_PER_SEC;
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
p[0]=1;for(RE int i=1;i<10000005;++i)p[i]=p[i-1]*base;
cin>>T;
while(T--){
cin>>t1>>t2>>s;
n=strlen(s);m1=strlen(t1);m2=strlen(t2);
// n=10000000;m1=9999999;m2=1;
// for(int i=1;i<=m1;i++)t1[i]=rand()%26+'a';
// for(int i=1;i<=m2;i++)t2[i]=rand()%26+'a';
// for(int i=1;i<=n;i++)s[i]=rand()%26+'a';
h0=h1[0]=h2[0]=0;ans=0;H.clear();
for(RE int i=1;i<=m2;++i)h0=h0*base+t2[i-1];
for(RE int i=1;i<=m1;++i)h1[i]=h1[i-1]*base+t1[i-1];
for(RE int i=0;i<=m1;++i)
++H[h1[i]*p[m1+m2-i]+h0*p[m1-i]+(h1[m1]-h1[i]*p[m1-i])];
for(RE int i=1;i<=n;++i){
h2[i]=h2[i-1]*base+s[i-1];
if(i>=m1+m2)ans+=H[h2[i]-h2[i-m1-m2]*p[m1+m2]];
}
cout<<ans<<'\n';
}
// double T2=clock()*1000/CLOCKS_PER_SEC;
// cout<<(T2-T1)<<"ms"<<endl;
return 0;
}
第七场
丢了一个队友(其实是没来)。
开02,看过了一堆大胆猜结论,一发A。队友签掉11,13。看04是数学题,跟来的一个队友找规律许久无果。队友放了,我开始想严谨做法,一下会了,过掉。此时已经2点。队友表示08可以写,讨论一通理清思路之后让他写(下面放的代码是我的赛后重构)。我一直在调05,知道是分类讨论但就是不全,最后也没过。垃圾题。
5道题排名92.
1002 Random Nim Game
Alice 和 Bob 做游戏,两人轮流操作。有 \(n\) 堆石子,每次操作者最优地选取一堆石子,然后等概率的从中取走若干颗(至少 \(1\) 颗,不超过总数),问先手获胜的概率。
Solution:如果不全为 \(1\),则概率为 \(\frac{1}{2}\);若全为 \(1\),则奇数时概率为 \(1\),偶数时概率为 \(0\)。证明归纳即可。
代码简单不放。
1004 Medians Strike Back
一个序列的中位数定义为:若长度为奇数,则为排序后中间的一个;若长度为偶数,则为排序后中间的两个出现次数较多的一个。一个序列的 shikness 定义为中位数出现的次数。一个序列的 nitness 定义为它所有连续子序列中 shikness 的最大值。求长度为 \(n\),值域为 \(\{1,2,3\}\) 的序列的 nitness 的最小值。
Solution:只要对每个 \(k\),找到一个下界 \(m_k\),使得对于长度大于等于 \(m_k\) 的序列,nitness 一定大于 \(k\)。然后二分找到第一个大于 \(n\) 的 \(m_k\) 即可。
对 \(k=2p-1\),一个长度为 \(4p\) 的序列中至少要有 \(2\) 个 \(2\),而序列中 \(2\) 的总数不能超过 \(k\),所以 \(m_k=4p\cdot p =k^2+2k+1\) 合乎条件。同时可以有形如 \(1 3 1 3 \cdots 1 3 2 2 1 3 1 3 \cdots 1 3 2 2 \cdots\) 的构造。
对 \(k=2p\) 也类似,\(m_k=(4p+2)\cdot p + (4p+1) =k^2+3k+1\)。
代码简单不放。
1005 Subsequence Not Substring
给定字符串 \(s\),求一个是 \(s\) 的子序列但不是 \(s\) 的子串的字符串,且字典序最小,或判断无解。
Solution:分类讨论。
- 无解的情况是 \(s\) 极长连续段的数目不超过 \(2\)。
- 如果 \(s\) 的最小字符拥有不止一个极长连续段,则答案为最长的连续段长度再加一个最小字符。
- 如果 \(s\) 的最小字符 \(x\) 是最后一个极长连续段,找到 \(s\) 的次小字符 \(y\)。
- 如果 \(x\) 与 \(y\) 相邻,且 \(y\) 只有一个极长连续段,则找到 \(s\) 的第三小字符 \(z\),答案是 \(zx\)。
- 否则,设与 \(x\) 相邻的 \(y\) 的极长连续段长度为 \(k\)(可能 \(k=0\)),则当 \(k\) 是最长的一个段时,答案为 \(k+1\) 个 \(y\);否则,答案为 \(k+1\) 个 \(y\) 加上一个 \(x\)。
- 如果 \(s\) 的最小字符 \(x\) 是倒数第二个段,找到 \(s\) 之前的最小字符 \(z\),并设 \(x\) 后面的段为 \(y\)。
- 如果 \(x\) 的段长度为 \(1\),当 \(z\) 有唯一一段且与 \(x\) 相邻时,若 \(z<y\),答案为这段 \(z\) 加上一个 \(y\);若 \(z=y\),答案为两段中较长的一段长度加一个 \(z\);若 \(z>y\),答案为 \(zy\)。当 \(z\) 拥有多段时,若 \(z>y\),答案还是 \(zy\);否则,同上面的第二种情形(考虑是否是最长段)。
- 如果 \(x\) 的段长度大于 \(1\),答案是 \(z\) 加上该段长度减一个 \(x\) 加上一个 \(y\)。
- 如果 \(s\) 的最小字符不是倒数两个段,不断找后缀最小值的段,如果不连续了就成为答案(新的段只取一个,前面都取),否则一直到最后,倒数第二个段少取一个,最后一个段只取一个。
不知道是不是写全了,反正代码过了。垃圾题。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int T,n,m,L[N],R[N],a[N],mn[N][20];char s[N];
vector<int> ans;
int query(int l,int r){
int x=log2(r-l+1);
if(a[mn[l][x]]<=a[mn[r-(1<<x)+1][x]])
return mn[l][x];
return mn[r-(1<<x)+1][x];
}
int main(){
scanf("%d",&T);
while(T--){
ans.clear();m=0;
scanf("%s",s+1);
n=strlen(s+1);s[n+1]='a'+26;
for(int i=2,l=1;i<=n+1;i++)
if(s[i]!=s[i-1]){
L[++m]=l;R[m]=i-1;l=i;
mn[m][0]=m;a[m]=s[i-1];
}
if(m<=2){printf("-1\n");continue;}
for(int j=1;(1<<j)<=m;j++)
for(int i=1;i<=m-(1<<j)+1;i++){
if(a[mn[i][j-1]]<=a[mn[i+(1<<j-1)][j-1]])
mn[i][j]=mn[i][j-1];
else mn[i][j]=mn[i+(1<<j-1)][j-1];
}
int lst=0;a[0]=127;
for(int i=1;i<=m-2;i++)if(a[i]<a[lst])lst=i;
ans.push_back(lst);
if(a[query(lst+1,m)]==a[lst]){
int mx=0;
for(int i=1;i<=m;i++)
if(a[i]==a[lst])mx=max(mx,R[i]-L[i]+1);
for(int i=0;i<=mx;i++)printf("%c",s[L[lst]]);
printf("\n");
continue;
}
while(1){
int now=query(lst+1,m);
if(now!=lst+1){
if(a[now]<a[lst]){
if(now==m-1&&L[now]!=R[now]){
if(a[now-1]==a[lst]){
printf("%c",s[L[lst]]);
for(int j=L[now];j<R[now];j++)printf("%c",s[j]);
printf("%c\n",s[L[m]]);
}else printf("%c%c\n",s[L[lst]],s[L[now]]);
break;
}
if(a[now-1]==a[lst]){
if(now==m-1&&a[now-1]>a[m]){
printf("%c%c\n",s[L[now-1]],s[L[m]]);
break;
}
int mx=0;
for(int j=1;j<=m;j++)
if(a[j]==a[lst])mx=max(mx,R[j]-L[j]+1);
for(int j=0;j<=R[now-1]-L[now-1]+1;j++)
printf("%c",s[L[lst]]);
if(R[now-1]-L[now-1]+1!=mx)printf("%c",s[L[now]]);
printf("\n");
}
else printf("%c%c\n",s[L[lst]],s[L[now]]);
break;
}
for(int i=0;i<ans.size();i++)
for(int j=L[ans[i]];j<=R[ans[i]];j++)
printf("%c",s[j]);
printf("%c\n",s[L[now]]);
break;
}
if(ans.size()==1&&now==m-1){
if(L[now]==R[now]){
if(a[lst]>a[m])printf("%c",s[L[lst]]);
else if(a[lst]==a[m]){
int mx=max(R[lst]-L[lst]+1,R[m]-L[m]+1);
for(int j=1;j<=mx;j++)printf("%c",s[L[lst]]);
}
else for(int j=L[lst];j<=R[lst];j++)printf("%c",s[j]);
printf("%c",s[L[m]]);
}
else{
if(a[lst]>a[now])printf("%c",s[L[lst]]);
else for(int j=L[lst];j<=R[lst];j++)printf("%c",s[j]);
for(int j=L[now];j<R[now];j++)printf("%c",s[j]);
printf("%c",s[L[m]]);
}
printf("\n");break;
}
if(now==m){
int len=ans.size();
for(int i=0;i<len-1;i++)
for(int j=L[ans[i]];j<=R[ans[i]];j++)printf("%c",s[j]);
for(int j=L[ans[len-1]];j<R[ans[len-1]];j++)printf("%c",s[j]);
printf("%c\n",s[L[now]]);
break;
}
ans.push_back(lst=now);
}
}
return 0;
}
1008 HEX-A-GONE Trails
一棵 \(n\) 个点的树,两个人分别在两个点上轮流行动,每次移向某个相邻的点。不能重复经过一个点(包括另一个人经过的点)。不能行动者判负,问先手是否必胜。
\(n \le 10^5\)。
Solution:找到两人之间的链,尝试走向链外是否能获胜。预处理出一个点向链外最多走的步数,并 ST 表预处理即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define getchar() (SS==TT&&(TT=(SS=BB)+fread(BB,1,1<<15,stdin),SS==TT)?EOF:*SS++)
char BB[1<<15],*SS=BB,*TT=BB;
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48){if(c=='-')f=-1;c=getchar();}
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
const int N=1e5+5;
int T,n,s,t,fa[N],vis[N],mx[N],a[N],m;vector<int> G[N];
struct ST{
int n,mx[N][20];
void pre(){
for(int j=1;(1<<j)<=n;j++)
for(int i=1;i<=n-(1<<j)+1;i++)
mx[i][j]=max(mx[i][j-1],mx[i+(1<<j-1)][j-1]);
}
int query(int l,int r){
int x=log2(r-l+1);
return max(mx[l][x],mx[r-(1<<x)+1][x]);
}
}st1,st2;
void dfs1(int u){for(int v:G[u])if(v!=fa[u])fa[v]=u,dfs1(v);}
void dfs2(int u,int rt,int len){
mx[rt]=max(mx[rt],len);vis[u]=1;
for(int v:G[u])if(!vis[v])dfs2(v,rt,len+1);
}
int main(){
T=read();
while(T--){
n=read();
for(int i=1;i<=n;i++)
vis[i]=mx[i]=0,G[i].clear();
s=read();t=read();
for(int i=1,u,v;i<n;i++){
u=read();v=read();
G[u].push_back(v);
G[v].push_back(u);
}
m=fa[t]=0;dfs1(t);
for(int v=s;v!=t;v=fa[v])a[++m]=v;
a[++m]=t;st1.n=st2.n=m;
for(int i=1;i<=m;i++)vis[a[i]]=1;
for(int i=1;i<=m;i++){
dfs2(a[i],i,0);
st1.mx[i][0]=mx[i]+(i-1);
st2.mx[i][0]=mx[i]+(m-i);
}
st1.pre();st2.pre();
int l=1,r=m;
while(l<r){
if((l-1)+mx[l]>st2.query(l+1,r)){printf("1\n");break;}
if(l==r-1){printf("0\n");break;}++l;
if(st1.query(l,r-1)<=(m-r)+mx[r]){printf("0\n");break;}
if(l==r-1){printf("1\n");break;}--r;
}
}
return 0;
}
1012 Landmine
一棵 \(n\) 个点的树,边有权,每个点有半径 \(r_i\),可以从一个点移动到半径以内的点。问从点 \(i=2,3,\cdots,n\) 开始,走到 \(1\) 的最小步数。
\(n \le 10^5\)。
Solution:倒着做一个 BFS,每次把能到达一个点的所有点加入队列。考虑点分树维护,每次从 \(i\) 开始跳父亲,在祖先 \(u\),把 \(u\) 子树内所有满足 \(r_j-dist(u,j) \ge dist(u,i)\) 的点 \(j\) 加入队列。将每个子树的点按这个值排序维护指针即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read(){
ll x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+5;
int T,n;ll r[N];
int head[N],nxt[N<<1],ver[N<<1],tot;ll val[N<<1];
void add(int u,int v,ll w){
ver[++tot]=v;val[tot]=w;
nxt[tot]=head[u];head[u]=tot;
}
int anc[N][20],dep[N];ll dis[N];
void dfs0(int u){
for(int i=head[u],v;i;i=nxt[i])
if((v=ver[i])!=anc[u][0]){
anc[v][0]=u;dep[v]=dep[u]+1;
dis[v]=dis[u]+val[i];dfs0(v);
}
}
void pre(){
for(int j=1;j<=19;j++)
for(int i=1;i<=n;i++)
anc[i][j]=anc[anc[i][j-1]][j-1];
}
int LCA(int u,int v){
if(dep[u]<dep[v])swap(u,v);int d=dep[u]-dep[v];
for(int i=19;i>=0;i--)if(d&(1<<i))u=anc[u][i];
if(u==v)return u;
for(int i=19;i>=0;i--)
if(anc[u][i]!=anc[v][i])u=anc[u][i],v=anc[v][i];
return anc[u][0];
}
ll dist(int u,int v){return dis[u]+dis[v]-2*dis[LCA(u,v)];}
int num,rt,vis[N],sz[N],mx[N],fa[N];
void csize(int u,int fa){
sz[u]=1;mx[u]=0;
for(int i=head[u],v;i;i=nxt[i])
if((v=ver[i])!=fa&&!vis[v])
csize(v,u),sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
mx[u]=max(mx[u],num-sz[u]);if(mx[u]<mx[rt])rt=u;
}
void dfs(int u){
vis[u]=1;
for(int i=head[u],v;i;i=nxt[i])if(!vis[v=ver[i]])
rt=0,num=sz[v],csize(v,-1),csize(rt,-1),fa[rt]=u,dfs(rt);
}
ll X[N];
bool cmp(int i,int j){return X[i]>X[j];}
queue<int> Q;vector<int> subt[N];int pos[N],in[N],ans[N];
void init(int n){
for(int i=1;i<=n;i++){
head[i]=vis[i]=anc[i][0]=in[i]=pos[i]=0;
ans[i]=-1;subt[i].clear();
}tot=0;
}
int main(){
T=read();
while(T--){
num=n=read();init(n);
for(int i=2;i<=n;i++)r[i]=read();
for(int i=1,u,v;i<n;i++){
u=read();v=read();ll w=read();
add(u,v,w);add(v,u,w);
}
dfs0(1);pre();
rt=0;mx[0]=1e9;csize(1,-1);csize(rt,-1);fa[rt]=0;dfs(rt);
for(int u=1;u<=n;u++)
for(int v=u;v;v=fa[v])
subt[v].push_back(u);
for(int u=1;u<=n;u++){
for(int j:subt[u])X[j]=r[j]-dist(j,u);
sort(subt[u].begin(),subt[u].end(),cmp);
}
ans[1]=0;Q.push(1);in[1]=1;
while(!Q.empty()){
int i=Q.front();Q.pop();
for(int u=i;u;u=fa[u]){
ll len=dist(i,u);
while(pos[u]<subt[u].size()){
int j=subt[u][pos[u]];
if(r[j]-dist(j,u)>=len){
if(!in[j])Q.push(j),ans[j]=ans[i]+1,in[j]=1;
++pos[u];
}
else break;
}
}
}
for(int i=2;i<=n;i++)printf("%d ",ans[i]);
printf("\n");
}
return 0;
}
第六场
有了新队友,看我C!
上来签掉01,然后看02,发现不是很会。继续往后看,04一眼点分治,写写写,过。队友说会02,然后T。我看02过了一堆,也写02,似乎是假做法,但是过了。此时2点。开始看05,发现又是一眼,二分过。然后来写03,中间队友过了08,过了07(套数据)。我的03写了巨大分类讨论,没想到最后在3点40过了!5道题,C!
总共9道题排名16。
1001 Count
求字符集大小 \(m\),长为 \(n\),有周期 \(k\) 的字符串数目。
Solution:若 \(n=k\),则答案为 \(m^n\);否则,答案为 \(m^{n-k}\)。但似乎不特判 \(n=k\) 也过了?代码简单不放。
1002 Pair Sum and Perfect Square
给定一个长为 \(n\) 的排列,\(q\) 次询问,问下标区间 \([L,R]\) 中有多少对数和为平方数。
\(n,q \le 10^5\)。
Solution:一个非常容易想到的 \(O(n \sqrt n \log n)\) 的做法是离线二维数点。直接跑出所有和为平方数的数对,用树状数组维护即可。但这个复杂度看上去不能过,但一发过了。
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define getchar() (SS==TT&&(TT=(SS=BB)+fread(BB,1,1<<15,stdin),SS==TT)?EOF:*SS++)
char BB[1<<15],*SS=BB,*TT=BB;
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48){if(c=='-')f=-1;c=getchar();}
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
const int N=1e5+5,P=998244353;
int T,n,a[N],b[N],q,ans[N];
struct range{int l,r,id;}r[N];
bool operator <(const range&a,const range&b){return a.r<b.r;}
struct BIT{
int c[N],n;
inline void init(){for(int i=1;i<=n;i++)c[i]=0;}
inline void add(int x){for(;x<=n;x+=x&-x)++c[x];}
inline int ask(int x){int res=0;for(;x;x-=x&-x)res+=c[x];return res;}
}B;
int main(){
T=read();
while(T--){
B.n=n=read();
for(register int i=1;i<=n;++i)
a[i]=read(),b[a[i]]=i;
q=read();
for(register int i=1;i<=q;++i)
r[i].l=read(),r[i].r=read(),r[i].id=i;
sort(r+1,r+q+1);B.init();
for(register int i=1,p=1;i<=n;++i){
for(register int j=1;j*j<=n+a[i];++j)
if(j*j-a[i]>0&&b[j*j-a[i]]<i)B.add(b[j*j-a[i]]);
while(r[p].r==i&&p<=q)ans[r[p].id]=B.ask(n)-B.ask(r[p].l-1),++p;
}
for(int i=1;i<=q;i++)printf("%d\n",ans[i]);
}
return 0;
}
1003 Vector
给定各维非负的四个三维向量 \(A_1,A_2,A_3,A_4\),问是否存在非负实数 \(x_1,x_2,x_3\),使 \(x_1A_1+x_2A_2+x_3A_3=A_4\)。
Solution:考虑给式子两边同时数乘一个向量,使得式子中两个未知数被消掉。也就是说乘以 \(A_1,A_2\) 的法向量 \(n_{12}\),得到 \(x_3A_3 \cdot n_{12}=A_4 \cdot n_{12}\)。那么就解出了 \(x_3\)。
但是要特判很多情况,因为当两边系数都为 \(0\) 的时候还不能判断。我的判断包含以下内容:
- \(A_1,A_2,A_3\) 均为零向量。判 \(A_4\) 是否为零向量。
- 恰有两个零向量。判剩下一个是否与 \(A_4\) 共线。
- 恰有一个零向量。此时分剩下两个是否共线讨论。共线很容易;不共线的情形,再取两个不共线的三维向量\(v_1,v_2\),用 \(A_1\) 与 \(v_1\),\(A_1\) 与 \(v_2\) ,\(A_2\) 与 \(v_1\),\(A_2\) 与 \(v_2\) 的法向量进行判定。
- 有两个向量共线。和上一种情况类似。
- 三个向量共面。先判断 \(A_4\) 是否也在这个面上,如果在,在三个中任取两个用上面的方法判定。
- 其他情况。用一开始提的方法判定就行。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48){if(c=='-')f=-1;c=getchar();}
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
typedef long long ll;
struct vec{
ll x,y,z;
bool empty(){return (x==0&&y==0&&z==0);}
}A,B,C,D;
bool line(vec a,vec b){return a.y*b.z-a.z*b.y==0&&b.x*a.z-b.z*a.x==0;}
bool plane(vec a,vec b,vec c){
return a.x*b.y*c.z+a.y*b.z*c.x+a.z*b.x*c.y==
a.z*b.y*c.x+a.x*b.z*c.y+a.y*b.x*c.z;
}
vec fa(vec a,vec b){return {a.y*b.z-a.z*b.y,b.x*a.z-b.z*a.x,a.x*b.y-a.y*b.x};}
ll operator *(const vec&a,const vec&b){return a.x*b.x+a.y*b.y+a.z*b.z;}
int T;ll p,q;
#define check p==0&&q!=0||p>0&&q<0||p<0&&q>0
#define finish {printf("NO\n");continue;}
bool CCF(vec A,vec B,vec D){
p=fa(A,{1,0,0})*B;q=fa(A,{1,0,0})*D;if(check)return false;
p=fa(A,{0,1,0})*B;q=fa(A,{0,1,0})*D;if(check)return false;
p=fa(B,{1,0,0})*A;q=fa(B,{1,0,0})*D;if(check)return false;
p=fa(B,{0,1,0})*A;q=fa(B,{0,1,0})*D;if(check)return false;
return true;
}
int main(){
T=read();
while(T--){
A.x=read();A.y=read();A.z=read();
B.x=read();B.y=read();B.z=read();
C.x=read();C.y=read();C.z=read();
D.x=read();D.y=read();D.z=read();
if(A.empty()&&B.empty()&&C.empty()){
if(!D.empty())finish;
printf("YES\n");continue;
}
if(A.empty()+B.empty()+C.empty()==2){
if(!B.empty())swap(A,B);
if(!C.empty())swap(A,C);
if(line(A,D))printf("YES\n");
else printf("NO\n");
continue;
}
if(A.empty()+B.empty()+C.empty()==1){
if(A.empty())swap(A,C);
if(B.empty())swap(B,C);
if(!plane(A,B,D))finish;
if(line(A,B)){
if(line(A,D))printf("YES\n");
else printf("NO\n");
continue;
}
printf(CCF(A,B,D)?"YES\n":"NO\n");
continue;
}
if(line(A,C))swap(B,C);
else if(line(B,C))swap(A,C);
if(line(A,B)){
if(!plane(A,C,D))finish;
if(line(A,C)){
if(line(A,D))printf("YES\n");
else printf("NO\n");
}
else{
printf(CCF(A,C,D)?"YES\n":"NO\n");
continue;
}
continue;
}
if(plane(A,B,C)){
if(!plane(A,B,D)){printf("NO\n");continue;}
printf(CCF(A,B,D)||CCF(B,C,D)||CCF(C,A,D)?"YES\n":"NO\n");
continue;
}
p=fa(A,B)*C;q=fa(A,B)*D;if(check)finish;
p=fa(B,C)*A;q=fa(B,C)*D;if(check)finish;
p=fa(C,A)*B;q=fa(C,A)*D;if(check)finish;
printf("YES\n");
}
return 0;
}
1004 Tree
给定一棵 \(n\) 个点的树,每个点上有 \(a,b,c\) 三种字符之一,求满足 \(a,b,c\) 数目相同的路径数目。
\(n \le 10^5\)。
Solution:一眼点分治。用两个参数表示根到一个点的路径:\(a\) 的数目乘 \(3\) 减去长度;\(b\) 的数目乘 \(3\) 减去长度。用 map 记录,复杂度 \(O(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n;char s[N];ll ans;
int head[N],nxt[N<<1],ver[N<<1],tot;
void add(int u,int v){ver[++tot]=v;nxt[tot]=head[u];head[u]=tot;}
int sum,rt,vis[N],sz[N],mx[N],A0,B0;
void csize(int u,int fa){
sz[u]=1;mx[u]=0;
for(int i=head[u],v;i;i=nxt[i])
if((v=ver[i])!=fa&&!vis[v])
csize(v,u),sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
mx[u]=max(mx[u],sum-sz[u]);if(mx[u]<mx[rt])rt=u;
}
map<pair<int,int>,ll> M;
queue<pair<int,int> > Q;
void cdist(int u,int fa,int A,int B){
if(A==0&&B==0)++ans;
ans+=M[{-A,-B}];Q.push({A-A0,B-B0});
for(int i=head[u],v;i;i=nxt[i])
if((v=ver[i])!=fa&&!vis[v])
cdist(v,u,A+3*(s[v]=='a')-1,B+3*(s[v]=='b')-1);
}
void dfs(int u){
vis[u]=1;A0=3*(s[u]=='a')-1,B0=3*(s[u]=='b')-1;
for(int i=head[u],v;i;i=nxt[i])
if(!vis[v=ver[i]]){
cdist(v,u,A0+3*(s[v]=='a')-1,B0+3*(s[v]=='b')-1);
while(!Q.empty())++M[Q.front()],Q.pop();
}
M.clear();
for(int i=head[u],v;i;i=nxt[i])if(!vis[v=ver[i]])
sum=sz[v],rt=0,csize(v,-1),csize(rt,-1),dfs(rt);
}
int main(){
scanf("%d",&n);
scanf("%s",s+1);
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
sum=n;rt=0;mx[rt]=1e9;
csize(1,-1);csize(rt,-1);dfs(rt);
printf("%lld\n",ans);
return 0;
}
1005 Meadow
给定一个 \(n\times m\) 的 01 矩阵,另外有一个 \(n\times m\) 的分数矩阵。如果一个点在某个 \(L \times L\) 的正方形中,则总得分加上 \(L\) 乘以该点的分数。求总的分数 \(\bmod 10^9+7\)。
\(n,m\le 1000\)。
Solution:枚举左上角,二分最大的 \(L\),二维前缀和预处理判定和贡献。
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define getchar() (SS==TT&&(TT=(SS=BB)+fread(BB,1,1<<15,stdin),SS==TT)?EOF:*SS++)
char BB[1<<15],*SS=BB,*TT=BB;
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48){if(c=='-')f=-1;c=getchar();}
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
const int N=1005,P=1e9+7;
int T,n,m,a[N][N],b[N][N],s[N][N],t[N][N],ans;
int f[N][N][3],g[N][N][3];
int main(){
T=read();
while(T--){
n=read();m=read();ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
a[i][j]=read();
s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
b[i][j]=read();
t[i][j]=(0ll+t[i][j-1]+t[i-1][j]-t[i-1][j-1]+b[i][j]+2*P)%P;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
g[i][j][0]=(g[i-1][j][0]+t[i][j])%P;
g[i][j][1]=(g[i][j-1][1]+t[i][j])%P;
g[i][j][2]=(g[i-1][j-1][2]+t[i][j])%P;
f[i][j][0]=(f[i-1][j][0]+1ll*i*t[i][j]%P)%P;
f[i][j][1]=(f[i][j-1][1]+1ll*j*t[i][j]%P)%P;
f[i][j][2]=(f[i-1][j-1][2]+1ll*min(i,j)*t[i][j]%P)%P;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
int L=1,R=min(n-i+1,m-j+1),k=0;
while(L<=R){
int mid=L+R>>1;
if(s[i+mid-1][j+mid-1]+s[i-1][j-1]
-s[i+mid-1][j-1]-s[i-1][j+mid-1]==mid*mid)
L=mid+1,k=mid;
else R=mid-1;
}
ans=(ans+0ll+(1ll*k*(k+1)/2)%P*t[i-1][j-1]%P
+(f[i+k-1][j+k-1][2]-f[i-1][j-1][2]-
1ll*min(i-1,j-1)*(g[i+k-1][j+k-1][2]-g[i-1][j-1][2]+P)%P+2*P)%P
+(f[i-1][j-1][0]-f[i+k-1][j-1][0]+
1ll*(i-1)*(g[i+k-1][j-1][0]-g[i-1][j-1][0]+P)%P+P)%P
+(f[i-1][j-1][1]-f[i-1][j+k-1][1]+
1ll*(j-1)*(g[i-1][j+k-1][1]-g[i-1][j-1][1]+P)%P+P)%P)%P;
}
printf("%d\n",ans);
}
return 0;
}
第五场
没和队友联系,然后发现只有我一个人在打。
开场签掉07,12,然后看01。发现可以枚举,写写写,WA。但是感觉大对无比,先放一下,同时开了06,调了几发过了。写09,被卡常加上此时过不了01心态很炸。copy了一个fread的板子终于过了09,然后又换了一个01的写法过了。此时3点。剩下的题里写了03和11,感觉都不太难。最后会了02的杜教筛,但是现学现卖写假了。7道题排名155.
1001 Typhoon
给定一条 \(m\) 个点的折线,\(n\) 个询问,每次询问一个点到折线上的点的最短距离。
\(n,m\le 10^4\)。
Solution:\(O(nm)\) 计算即可。计算点到线段的距离时采用矢量法,否则会WA。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=10005;
struct point{ll x,y;}p[N],t;
inline ld DIS(point a,point b){
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
inline ld dist(point a,point b,point c){
ld cross=(c.x-b.x)*(a.x-b.x)+(c.y-b.y)*(a.y-b.y);
if(cross<=0)return DIS(a,b);
ld d2=(c.x-b.x)*(c.x-b.x)+(c.y-b.y)*(c.y-b.y);
if(cross>=d2)return DIS(a,c);
ld r=cross/d2;
ld px=b.x+(c.x-b.x)*r,py=b.y+(c.y-b.y)*r;
return sqrt((a.x-px)*(a.x-px)+(a.y-py)*(a.y-py));
}
inline ld min(ld a,ld b){return a<b?a:b;}
int m,n;ld dis[N];
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=m;++i)scanf("%lld%lld",&p[i].x,&p[i].y);
for(register int i=1;i<=n;++i){
scanf("%lld%lld",&t.x,&t.y);
ld ans=DIS(t,p[1]);
for(register int j=1;j<m;++j)
ans=min(ans,dist(t,p[j],p[j+1]));
printf("%.4Lf\n",ans);
}
return 0;
}
1002 GCD Magic
求
\]
\(1\le n \le 10^9,0 \le k \le 10\)。
Solution:记 \(f(x)=(2^x-1)^k\),熟知 \(\gcd(f(i),f(j))=f(\gcd(i,j))\),则
ans&=\sum_{i=1}^{n} \sum_{j=1}^{n} f(\gcd(i,j))\\&=\sum_{d=1}^n f(d)\sum_{i=1}^{\lfloor \frac{n}{d}\rfloor} \sum_{j=1}^{\lfloor \frac{n}{d}\rfloor}[\gcd(i,j)=1]\\&=\sum_{d=1}^n f(d)\sum_{i=1}^{\lfloor \frac{n}{d}\rfloor} \sum_{j=1}^{\lfloor \frac{n}{d}\rfloor}\sum_{t|(i,j)}\mu(t)\\&=\sum_{d=1}^n f(d)\sum_{t=1}^{\lfloor \frac{n}{d}\rfloor}\lfloor \frac{n}{dt}\rfloor^2\mu(t)\\&=\sum_{T=1}^n\lfloor \frac{n}{T}\rfloor^2\sum_{d|T}f(d)\mu(\frac{T}{d})
\end{aligned}\]
令 \(g=f \ast \mu,S(n) = \sum_{i=1}^n g(i)\),尝试用杜教筛求 \(S\)。让 \(g\) 和 \(1\) 卷。
\]
\(f\) 的前缀和可以二项式展开后等比数列求和。杜教筛可以做到 \(O(n^{\frac{2}{3}})\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int P=998244353,N=1e6+5;
int power(int a,int b){
int c=1;
for(;b;b>>=1){
if(b&1)c=1ll*c*a%P;
a=1ll*a*a%P;
}
return c;
}
int flag[N],p[N],tot;
int T,n,k,C[15][15],f[N],mu[N],s[N];
map<int,int> M;
int F(int n){
int res=(k&1)?(P-n):n;
for(int i=1;i<=k;i++){
int x=1ll*C[k][i]*(power((1<<i),n+1)-(1<<i)+P)%P*power((1<<i)-1,P-2)%P;
if((k-i)&1)res=(res-x+P)%P;else res=(res+x)%P;
}
return res;
}
int S(int n){
if(n<N)return s[n];
if(M[n])return M[n];
int res=F(n);
for(int l=2,r=0;l<=n;l=r+1){
r=n/(n/l);
res=(res-1ll*(r-l+1)*S(n/l)%P+P)%P;
}
return M[n]=res;
}
void init(){
C[0][0]=1;
for(int i=1;i<=12;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=C[i-1][j-1]+C[i-1][j];
}
mu[1]=1;
for(int i=2;i<N;i++){
if(!flag[i])p[++tot]=i,mu[i]=-1;
for(int j=1;j<=tot&&i*p[j]<N;j++){
flag[i*p[j]]=1;
if(i%p[j]==0){mu[i*p[j]]=0;break;}
mu[i*p[j]]=-mu[i];
}
}
}
int main(){
init();
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&k);
M.clear();
for(int i=1,now=1;i<N;i++){
now=2*now%P;f[i]=1;s[i]=0;
for(int j=1;j<=k;j++)f[i]=1ll*f[i]*(now-1)%P;
}
for(int i=1;i<N;i++)if(mu[i]!=0)
for(int j=1;i*j<N;j++)
s[i*j]=(s[i*j]+1ll*mu[i]*f[j]+P)%P;
for(int i=2;i<N;i++)s[i]=(s[i]+s[i-1])%P;
int ans=0;
for(int l=1,r=0,lst=0;l<=n;l=r+1){
r=n/(n/l);int cur=S(r);
ans=(ans+1ll*(n/l)*(n/l)%P*(cur-lst+P)%P)%P;
l=r+1;lst=cur;
}
printf("%d\n",ans);
}
return 0;
}
1003/1004 String Magic
定义 \(f(S)\) 为字符串 \(S\) 中有两个相同的回文串连接形成的串。对给定的 \(S\),Easy Version 要求 \(f(S)\),Hard Version 要对 \(S\) 的所有前缀 \(T\) 求 \(f(T)\)。
\(|S| \le 10^5\)。
Solution:Easy Version 可以 Manacher 加二维数点解决,只要从中心开始统计答案即可。
Hard Version 考虑使用 PAM,每次产生一个新的回文串,都判断一下是否合法,这可以 Hash 解决。然后在树上 DFS 求出每个回文串合乎条件的后缀数目。最后,每个前缀相比前一个前缀多出的答案,就是这个位置最长后缀回文串合乎条件的后缀数目,累加入答案即可。时间复杂度 \(O(n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=2e5+5;
int T,n,q[N];char s[N];ull p[N],pre[N],suf[N],base=131;
int cnt[N],trans[N][26],len[N],fail[N],flag[N],tot,lst;
vector<int> son[N];int val[N];
void Hash(){
pre[0]=suf[n+1]=0;p[0]=1;
for(int i=1;i<=n;i++)pre[i]=pre[i-1]*base+s[i],p[i]=p[i-1]*base;
for(int i=n;i>=1;i--)suf[i]=suf[i+1]*base+s[i];
}
ull h1(int l,int r){return pre[r]-pre[l-1]*p[r-l+1];}
ull h2(int l,int r){return suf[l]-suf[r+1]*p[r-l+1];}
bool check(int l,int r){
if((r-l)%2==0)return false;int mid=(l+r)>>1;
return h1(l,mid)==h1(mid+1,r)&&h1(l,mid)==h2(l,mid);
}
int node(int l){
++tot;
for(int j=0;j<26;j++)trans[tot][j]=0;
len[tot]=l;fail[tot]=cnt[tot]=0;
return tot;
}
void init(){
memset(flag,0,sizeof(flag));
memset(val,0,sizeof(val));
for(int i=0;i<=tot;i++)son[i].clear();
tot=-1;lst=0;node(0);node(-1);fail[0]=1;
}
int getfail(int x,int y){
while(s[x-len[y]-1]!=s[x])y=fail[y];
return y;
}
void dfs(int u){for(int v:son[u])val[v]=val[u]+flag[v],dfs(v);}
int main(){
scanf("%d",&T);
while(T--){
scanf("%s",s+1);n=strlen(s+1);
init();Hash();
for(int i=1;i<=n;i++){
int now=getfail(i,lst),c=s[i]-'a';
if(!trans[now][c]){
int x=node(len[now]+2);
flag[x]=check(i-len[now]-1,i);
fail[x]=trans[getfail(i,fail[now])][c];
trans[now][c]=x;
}
lst=trans[now][c];q[i]=lst;
}
for(int i=0;i<=tot;i++){
if(i!=1)son[fail[i]].push_back(i);
}
val[1]=flag[1];dfs(1);int ans=0;
for(int i=1;i<=n;i++)printf("%d ",ans+=val[q[i]]);
printf("\n");
}
return 0;
}
1005 Snake
把 \(n\) 个数分成 \(m\) 组,每组内再排列,要求每组都不超过 \(k\) 个数,求方案数。
\(n,m,k \le 10^6\)。
Solution:考虑生成函数。\(m=1,k=INF\) 的答案是 \(n!\),其指数型生成函数为 \(\frac{x}{1-x}\)。加上 \(k\) 的限制,得到 \(\frac{(1-x^k)x}{1-x}\)。再加上 \(m\) 的限制,得到 \(\frac{(1-x^k)^mx^m}{m!(1-x)^m}\)。答案是它的第 \(n\) 项系数乘 \(n!\),二项式展开求即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+50,P=998244353;
int T,n,m,k,ans,fac[N],facinv[N];
int power(int a,int b){
int c=1;
for(;b;b>>=1){
if(b&1)c=1ll*c*a%P;
a=1ll*a*a%P;
}
return c;
}
int C(int n,int m){return 1ll*fac[n]*facinv[m]%P*facinv[n-m]%P;}
int main(){
fac[0]=facinv[0]=1;
for(int i=1;i<N;i++){
fac[i]=1ll*fac[i-1]*i%P;
facinv[i]=power(fac[i],P-2);
}
scanf("%d",&T);
while(T--){
ans=0;
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<=m;i++){
int t=n-m-i*k;
if(t<0)break;
if(i&1)ans=(ans-1ll*C(m,i)*C(m+t-1,t)%P+P)%P;
else ans=(ans+1ll*C(m,i)*C(m+t-1,t)%P)%P;
}
printf("%d\n",1ll*ans*fac[n]%P*facinv[m]%P);
}
return 0;
}
1006 Touhou Red Red Blue
有一列 \(n\) 张卡牌,包含 R,G,B 三种。同时还有两个空。一次考虑卡牌,可以丢掉或者选取。选取时,如果 \(空1\) 为空则放入,否则如果 \(空2\) 为空则放入,再否则,考虑两个空内的卡牌与选取卡牌的颜色:
- 如果全相同,得 \(1\) 分,在 \(空1\) 中随便放一个颜色的卡牌。
- 如果全不同,在 \(空1\) 和 \(空2\) 中随便放一个颜色的卡牌。
- 否则,丢掉 \(空1\) 中的卡牌,将 \(空2\) 中的卡牌放入 \(空1\),选取的卡牌放入 \(空2\)。
问最大得分。
\(n \le 10^5\)。
Solution:DP,按照题意模拟决策即可。注意空位为空不适合作为状态,所以初始值很多。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int T,n,dp[N][3][3],dic[130],a[N],app[3],ans;char s[N];
int main(){
dic['R']=0;dic['G']=1;dic['B']=2;
scanf("%d",&T);
while(T--){
memset(dp,-0x3f,sizeof(dp));ans=0;
scanf("%s",s+1);n=strlen(s+1);
if(n<=2){
printf("0\n");
continue;
}
for(int i=1;i<=n;i++)a[i]=dic[s[i]];
app[0]=app[1]=app[2]=0;app[a[1]]=1;
for(int i=2;i<=n;i++){
if(app[0])dp[i][0][a[i]]=0;
if(app[1])dp[i][1][a[i]]=0;
if(app[2])dp[i][2][a[i]]=0;
}
for(int i=2;i<n;i++){
for(int j=0;j<3;j++)
for(int k=0;k<3;k++){
if(a[i+1]!=j&&a[i+1]!=k&&j!=k){
for(int x=0;x<3;x++)
for(int y=0;y<3;y++)
dp[i+1][x][y]=max(dp[i+1][x][y],dp[i][j][k]);
}
else if(a[i+1]==j&&a[i+1]==k){
ans=max(ans,dp[i][j][k]+1);
if(i==n-1)continue;
for(int x=0;x<3;x++)dp[i+2][x][a[i+2]]=
max(dp[i+2][x][a[i+2]],dp[i][j][k]+1);
}
else dp[i+1][k][a[i+1]]=max(dp[i+1][k][a[i+1]],dp[i][j][k]);
dp[i+1][j][k]=max(dp[i+1][j][k],dp[i][j][k]);
}
}
for(int j=0;j<3;j++)for(int k=0;k<3;k++)ans=max(ans,dp[n][j][k]);
printf("%d\n",ans);
}
return 0;
}
1010 Cut The Tree
给定一棵 \(n\) 个点的树,点有权。Alice 和 Bob 做游戏,首先 Alice 断一条边得到两棵树,然后 Bob 选一棵,Alice 选另一棵。两人分别在自己的树上选择两个权值异或起来作为自己的得分。游戏的总得分是 Bob 的得分减去 Alice 的得分。Bob 希望尽量小,Alice 希望尽量大,问最终得分。
\(n \le 10^5\)。
Solution:显然两人最后一步都会尽可能大,然后得分一定为正,所以只用枚举所断开的边,然后求出两部分各自的最大值,差的绝对值的最小值就是答案。
求两个数异或最大当然使用 01Trie。子树内部可以树上启发式合并。子树外,首先求出全局最大值和两个点,不为这两个点的祖先的点的最大值就是全局最大值。是祖先的构成两条链,从上往下走,每次加入子树外的点即可。前一步时间复杂度 \(O(n\log n\log v)\),后一步 \(O(n\log v)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define getchar() (SS==TT&&(TT=(SS=BB)+fread(BB,1,1<<15,stdin),SS==TT)?EOF:*SS++)
char BB[1<<15],*SS=BB,*TT=BB;
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48){if(c=='-')f=-1;c=getchar();}
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
const int N=2e5+5,M=1e7+5;
int T,n,fa[N],w[N],L[N],R[N],dfn,id[N],sz[N],son[N],a[N],b[N],vis[N],ans;
vector<int> G[N];
struct Trie{
int tr[M][2],ed[M],st[N],top,tot,ans;
void init(){
while(top)ed[st[top--]]=0;
for(int i=1;i<=tot;i++)tr[i][0]=tr[i][1]=0;
tot=1;ans=0;
}
int query(int x){
if(tot==1)return 0;
int p=1,res=0;
for(int i=29;i>=0;--i){
int c=(x>>i)&1;
if(tr[p][c^1])p=tr[p][c^1],res|=(1<<i);
else p=tr[p][c];
}
return ed[p];
}
void insert(int x,int id){
int p=1;
for(int i=29;i>=0;--i){
int c=(x>>i)&1;
if(!tr[p][c])tr[p][c]=++tot;
p=tr[p][c];
}ed[p]=id;st[++top]=p;
ans=max(ans,x^w[query(x)]);
}
}W;
void dfs1(int u){
sz[u]=1;L[u]=++dfn;id[dfn]=u;
for(int v:G[u])if(v!=fa[u]){
fa[v]=u;dfs1(v);sz[u]+=sz[v];
if(sz[v]>sz[son[u]])son[u]=v;
}R[u]=dfn;
}
void dfs2(int u,int opt){
for(int v:G[u])if(v!=fa[u]&&v!=son[u])dfs2(v,0);
if(son[u])dfs2(son[u],1);
W.insert(w[u],u);
for(int v:G[u])if(v!=fa[u]&&v!=son[u])
for(int j=L[v];j<=R[v];j++)
W.insert(w[id[j]],id[j]);
a[u]=W.ans;
if(!opt)W.init();
}
void dfs3(int u){W.insert(w[u],u);for(int v:G[u])if(v!=fa[u])dfs3(v);}
void dfs4(int u,int opt){
int v0=0;
for(int v:G[u])if(v!=fa[u]&&vis[v]==opt){v0=v;break;}
if(!v0)return;W.insert(w[u],u);
for(int v:G[u])if(v!=fa[u]&&vis[v]!=opt)dfs3(v);
b[v0]=W.ans;dfs4(v0,opt);
}
void init(){
for(int i=1;i<=n;i++){G[i].clear();son[i]=a[i]=b[i]=vis[i]=0;}
dfn=0;ans=2e9;W.init();
}
int main(){
T=read();
while(T--){
n=read();init();
for(int i=1;i<=n;i++)w[i]=read();
for(int i=1,u,v;i<n;i++){
u=read();v=read();
G[u].push_back(v);G[v].push_back(u);
}
dfs1(1);dfs2(1,0);
int mu=1,mv=1,mx=0;
for(int i=1;i<=n;i++){
W.insert(w[i],i);int j=W.query(w[i]);
if((w[i]^w[j])>mx)mx=w[i]^w[j],mu=j,mv=i;
}
for(int u=mu;u!=1;u=fa[u])vis[u]=1;W.init();dfs4(1,1);
for(int v=mv;v!=1;v=fa[v])vis[v]=2;W.init();dfs4(1,2);
for(int i=2;i<=n;i++)if(!vis[i])b[i]=mx;
for(int i=2;i<=n;i++)ans=min(ans,abs(a[i]-b[i]));
printf("%d\n",ans);
}
return 0;
}
1011 Cactus Circuit
一个 \(n\) 个点的仙人掌,每条边有一个耐久(有效时间),现在要为每条边选择一个启动时间,使得有效的边连通所有点的时间尽可能长。求这个时间。
\(n \le 10^5\)。
Solution:答案是所有的桥的耐久,和所有环上最小两个值的和,和所有环上第三小值的最小值。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define getchar() (SS==TT&&(TT=(SS=BB)+fread(BB,1,1<<15,stdin),SS==TT)?EOF:*SS++)
char BB[1<<15],*SS=BB,*TT=BB;
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48){if(c=='-')f=-1;c=getchar();}
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
const int N=1e5+5,M=4e5+5;
int T,n,m,dfn[N],low[N],st[N],top,dfncnt,cnt;ll ans;
int head[N],nxt[M],ver[M],tot;ll val[M];
set<int> S[N];map<pair<int,int>,ll> mp;
void add(int u,int v,int w){
ver[++tot]=v;val[tot]=w;
nxt[tot]=head[u];head[u]=tot;
ver[++tot]=u;val[tot]=w;
nxt[tot]=head[v];head[v]=tot;
}
void tarjan(int u,int in_edge){
low[u]=dfn[u]=++dfncnt;st[++top]=u;
for(int i=head[u],v;i;i=nxt[i])
if(i!=(in_edge^1)){
if(!dfn[v=ver[i]]){
tarjan(v,i);low[u]=min(low[u],low[v]);
if(low[v]>dfn[u])ans=min(ans,val[i]);
}
else low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u]){
++cnt;int v;
do S[cnt].insert(v=st[top--]); while(v!=u);
}
}
int main(){
T=read();
while(T--){
n=read();m=read();
memset(head,0,sizeof(head));
memset(dfn,0,sizeof(dfn));
mp.clear();ans=1e18;dfncnt=cnt=top=0;tot=1;
for(int i=1,u,v,w;i<=m;i++){
u=read();v=read();w=read();
if(u>v)swap(u,v);mp[{u,v}]+=w;
}
for(auto x:mp)add(x.first.first,x.first.second,x.second);
tarjan(1,0);
for(int i=1;i<=cnt;i++){
ll mn1=1e18,mn2=1e18,mn3=1e18;
while(!S[i].empty()){
int u=*S[i].begin();
for(int j=head[u],v;j;j=nxt[j]){
if(S[i].find(v=ver[j])!=S[i].end()){
if(val[j]<mn1)mn3=mn2,mn2=mn1,mn1=val[j];
else if(val[j]<mn2)mn3=mn2,mn2=val[j];
else if(val[j]<mn3)mn3=val[j];
}
}
S[i].erase(S[i].begin());
}
S[i].clear();
ans=min(ans,max(mn1+mn2,mn3));
}
printf("%lld\n",ans);
}
return 0;
}
1012 Counting Stars
\(n\) 个点,\(m\) 条边的图,求 \(k+1\) 个点的菊花图数目 \(cnt_k\)。只用输出 \(cnt_2\text{ xor } cnt_3\text{ xor } \cdots \text{ xor } cnt_{n-1}\)。
\(n,m \le 10^6\)。
Solution:直接枚举中心即可。代码不放。
第二场
2023-7-20
第一次 ACM 比赛的体验呢。还是比较不错的。
一上来就先开01,想了二十多分钟过了。然后看07,一眼bitset,但是HDU的评测机有点慌,写了发现是WA不是T,那就行,改改过了。看05想了一会发现不会。随便看看,发现08好像不难,写了一个DDP,T了。算复杂度发现很离谱。放了。后面的时间比较摆,但还是会了一个05。
一个月后补的,印象不深了,但是队友很C,最后过了10个题,排名31。
1001 Alice Game
一段长为 \(n\) 的序列,两人轮流操作。每次操作,可以选取序列中一段长为 \(k\) 且不在两端的区间,将其删掉,得到两个新的序列。也可以直接删掉一个长度不超过 \(k\) 的序列。不能操作者判负。问谁必胜。
\(0\le n \le 10^9,2\le k \le 10^7\)。
Solution:我不知道。虽然这个题是我写的,而且一发就过了,但是我在写题解时发现自己的结论是错的。
后来看了官方题解,答案是当且仅当 \(n \bmod (4k+10)==k+1\) 时后手胜。而我的条件是 \(n \bmod (4k+2)==k+1\) 或 \(4k+2 | n\)。所以这个代码怎么过的呢?~~
了转反,std先写 \(k-=2\),然后 \(n\) 模 \(4k+10\),当余 \(k+3\) 时后手胜。我写 \(n\) 模 \(4k+2\) 余 \(k+1,0\) 时后手胜,所以没全错,只是数据少了一种情形。
推导的过程其实就是拿 SG 函数硬推就行了。
代码太简单,不放了。
1005 Or
给定两个长为 \(n\) 的序列 \(a,b\),\(m\) 组询问 \(l,r\),求 \(\oplus_{i=l}^{r} \oplus_{j=i}^{r}(a_i+\sum_{k=i+1}^{j}b_k)\)。只用输出 \(\sum_{i=1}^{m} ans_i \times 233^i \bmod 998244353\),这里
\(ans_i\) 表示第 \(i\) 组询问的答案。
\(1\le n \le 10^5,1\le m \le 10^6,0\le a_i \le 5\times 10^8,0\le b_i \le 5000\)。
Solution:按位处理。试图找出 \(a_i\) 要加 \(b_j\) 到哪里在能使这一位有 \(1\)。然后用一个 ST 表就可以解决问题。
先换成前缀和的形式,用 \(b_i\) 表示实际的 \(b\) 的前 \(i\) 项和,\(a_i-b_i+2^{30}\) 代替 \(a_i\),则新的 \(a_i+b_j\) 在 \(j \ge i\) 时就可以代表原来的 \(a_i+\sum_{k=i+1}^{j} b_j\)。
要使得 \(a_i\) 与某个 \(b_j\) 相加,第 \(k\) 位是 \(1\),则需要 \(a_i\) 与 \(b_j\) 的第 \(k\) 位相同,且更低位相加进位;或者第 \(k\) 位不同,且更低位相加不进位。那么对所有低位离散化,建线段树,在每个权值上记下最小下标。扫到 \(a_i\) 时二分查找可用的区间即可。我开了两棵线段树来解决,实际可以不用。
点击查看代码
#include<bits/stdc++.h>
#define RE register
using namespace std;
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x;
}
const int N=1e5+5,M=1e6+5,base=233,P=998244353,INF=2147483647;
int T,n,m,a[N],b[N],x[N],nxt[N],st[N][20],q[M][2],ans[M];long long res;
#define ls p<<1
#define rs p<<1|1
#define mid ((l+r)>>1)
int mn[N<<2];
inline void modify(int p,int l,int r,int x,int v){
if(l==r){mn[p]=v;return;}
if(x<=mid)modify(ls,l,mid,x,v);
else modify(rs,mid+1,r,x,v);
mn[p]=min(mn[ls],mn[rs]);
}
inline int query(int p,int l,int r,int L,int R){
if(l>=L&&r<=R)return mn[p];
int res=INF;
if(L<=mid)res=min(res,query(ls,l,mid,L,R));
if(R>mid)res=min(res,query(rs,mid+1,r,L,R));
return res;
}
int main(){
T=read();
while(T--){
n=read();m=read();res=0;
for(RE int i=1;i<=n;++i)a[i]=read();
for(RE int i=1;i<=n;++i)b[i]=b[i-1]+read();
for(RE int i=1;i<=n;++i)a[i]=a[i]-b[i]+(1<<30);
for(RE int i=1;i<=m;++i){q[i][0]=read();q[i][1]=read();ans[i]=0;}
for(RE int k=0;k<30;++k){
int C=(1<<k)-1;
for(RE int i=1;i<=n;++i)x[i]=b[i]&C;
sort(x+1,x+n+1);int t=unique(x+1,x+n+1)-x-1;
for(RE int i=1;i<=n;++i)nxt[i]=INF;
for(RE int i=1;i<=t*4;++i)mn[i]=INF;
for(RE int i=n;i>=1;--i){
int y=lower_bound(x+1,x+t+1,b[i]&C)-x;
if((b[i]>>k)&1)modify(1,1,t,y,i);
int val=C-(a[i]&C);
int p1=upper_bound(x+1,x+t+1,val)-x-1,
p2=lower_bound(x+1,x+t+1,val+1)-x;
if(p1>=1)p1=query(1,1,t,1,p1);else p1=INF;
if(p2<=t)p2=query(1,1,t,p2,t);else p2=INF;
if(!((a[i]>>k)&1))nxt[i]=min(nxt[i],p1);
else nxt[i]=min(nxt[i],p2);
}
for(RE int i=1;i<=t*4;++i)mn[i]=INF;
for(RE int i=n;i>=1;--i){
int y=lower_bound(x+1,x+t+1,b[i]&C)-x;
if(!((b[i]>>k)&1))modify(1,1,t,y,i);
int val=C-(a[i]&C);
int p1=upper_bound(x+1,x+t+1,val)-x-1,
p2=lower_bound(x+1,x+t+1,val+1)-x;
if(p1>=1)p1=query(1,1,t,1,p1);else p1=INF;
if(p2<=t)p2=query(1,1,t,p2,t);else p2=INF;
if((a[i]>>k)&1)nxt[i]=min(nxt[i],p1);
else nxt[i]=min(nxt[i],p2);
}
for(RE int i=1;i<=n;++i)st[i][0]=nxt[i];
for(RE int j=1;(1<<j)<=n;++j)
for(int i=1;i<=n-(1<<j)+1;++i)
st[i][j]=min(st[i][j-1],st[i+(1<<j-1)][j-1]);
for(RE int i=1;i<=m;++i){
int l=q[i][0],r=q[i][1],x=log2(r-l+1);
if(min(st[l][x],st[r-(1<<x)+1][x])<=r)ans[i]|=(1<<k);
}
}
for(RE int i=m;i>=0;--i)res=(res*base%P+ans[i])%P;
printf("%lld\n",res);
}
return 0;
}
1007 foreverlasting and fried-chicken
给定一个点数为 \(n\) 的图,求如图所示的子图数目。
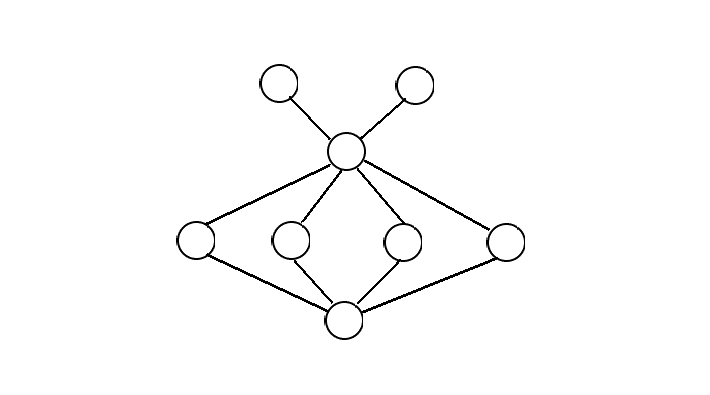
\(1\le n \le 1000, \sum n \le 3000\)。
Solution:枚举度为 \(4\) 和 \(6\) 的两个点,用 bitset 求交,然后做一个简单的计数。注意这两个点之间的边不能计入。复杂度有点悬,但能过。
代码简单不放。
1008 Hello World 3 Pro Max
长为 \(n\) 的字符串中,\(h,e,l,o,w,r,d\) 每个字符有一个出现概率。有 \(m\) 次修改和询问操作,修改为确定某个位置,询问为问一个区间的字符串中子序列 \(helloworld\) 的期望数。
\(1\le n,q\le 5 \times 10^4\)。
Solution:DDP板子。我写了,队友卡卡常过了。然后就是正解?
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+5,P=1e9+7;
int T,n,m,a[N],p[8],p0[8],s,dic[130];string ch,t=" helloworld";
int power(int a,int b){
int c=1;
for(;b;b>>=1){
if(b&1)c=1ll*c*a%P;
a=1ll*a*a%P;
}
return c;
}
struct Matrix{
int a[11][11];
Matrix(){memset(a,0,sizeof(a));}
Matrix operator *(const Matrix&b)const{
Matrix c;
for(int i=0;i<11;i++)
for(int j=i;j<11;j++)
for(int k=i;k<=j;k++)
c.a[i][j]=(c.a[i][j]+1ll*a[i][k]*b.a[k][j]%P)%P;
return c;
}
}tr[N<<2];
void init(int x,Matrix&c){
if(x==0)for(int i=1;i<=7;i++)p0[i]=p[i];
else{for(int i=1;i<=7;i++)p0[i]=0;p0[x]=1;}
for(int i=0;i<11;i++)c.a[i][i]=1;
for(int i=0;i<10;i++)c.a[i][i+1]=p0[dic[t[i+1]]];
}
#define ls p<<1
#define rs p<<1|1
#define mid ((l+r)>>1)
void build(int p,int l,int r){
if(l==r){init(0,tr[p]);return;}
build(ls,l,mid);build(rs,mid+1,r);
tr[p]=tr[ls]*tr[rs];
}
void modify(int p,int l,int r,int x,int v){
if(l==r){init(v,tr[p]);return;}
if(x<=mid)modify(ls,l,mid,x,v);
else modify(rs,mid+1,r,x,v);
tr[p]=tr[ls]*tr[rs];
}
Matrix query(int p,int l,int r,int L,int R){
if(l>=L&&r<=R)return tr[p];
if(R<=mid)return query(ls,l,mid,L,R);
if(L>mid)return query(rs,mid+1,r,L,R);
return query(ls,l,mid,L,R)*query(rs,mid+1,r,L,R);
}
int main(){
dic['h']=1;dic['e']=2;dic['l']=3;dic['o']=4;
dic['w']=5;dic['r']=6;dic['d']=7;
ios::sync_with_stdio(false);
cin>>T;
while(T--){
cin>>n;s=0;
for(int i=1;i<=7;i++){cin>>p[i];s+=p[i];}
s=power(s,P-2);for(int i=1;i<=n;i++)p[i]=1ll*p[i]*s%P;
build(1,1,n);cin>>m;
for(int i=1,op,l,r;i<=m;i++){
cin>>op;
if(op==1){
cin>>l>>ch;
modify(1,1,n,l,dic[ch[0]]);
}
else{
cin>>l>>r;
Matrix tmp;tmp.a[0][0]=1;
tmp=tmp*query(1,1,n,l,r);
printf("%d\n",tmp.a[0][10]);
}
}
}
return 0;
}
Competition Set - 2023杭电多校的更多相关文章
- 可持久化线段树的学习(区间第k大和查询历史版本的数据)(杭电多校赛第二场1011)
以前我们学习了线段树可以知道,线段树的每一个节点都储存的是一段区间,所以线段树可以做简单的区间查询,更改等简单的操作. 而后面再做有些题目,就可能会碰到一种回退的操作.这里的回退是指回到未做各种操作之 ...
- 2018 Multi-University Training Contest 1 杭电多校第一场
抱着可能杭电的多校1比牛客的多校1更恐怖的想法 看到三道签到题 幸福的都快哭出来了好吗 1001 Maximum Multiple(hdoj 6298) 链接:http://acm.hdu.edu. ...
- 2017杭电多校第五场11Rikka with Competition
Rikka with Competition Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/O ...
- 2018 Multi-University Training Contest 9 杭电多校第九场 (有坑待补)
咕咕咕了太久 多校博客直接从第三场跳到了第九场orz 见谅见谅(会补的!) 明明最后看下来是dp场 但是硬生生被我们做成了组合数专场…… 听说jls把我们用组合数做的题都用dp来了遍 这里只放了用组 ...
- 2018 Multi-University Training Contest 2 杭电多校第二场
开始逐渐习惯被多校虐orz 菜是原罪 1004 Game (hdoj 6312) 链接:http://acm.hdu.edu.cn/showproblem.php?pid=6312 虽然披着 ...
- 2019杭电多校&CCPC网络赛&大一总结
多校结束了, 网络赛结束了.发现自己还是太菜了,多校基本就是爆零和签到徘徊,第一次打这种高强度的比赛, 全英文,知识点又很广,充分暴露了自己菜的事实,发现数学还是很重要的.还是要多刷题,少玩游戏. 网 ...
- HDU 4941 Magical Forest(map映射+二分查找)杭电多校训练赛第七场1007
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4941 解题报告:给你一个n*m的矩阵,矩阵的一些方格中有水果,每个水果有一个能量值,现在有三种操作,第 ...
- HDU 4902 Nice boat 2014杭电多校训练赛第四场F题(线段树区间更新)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4902 解题报告:输入一个序列,然后有q次操作,操作有两种,第一种是把区间 (l,r) 变成x,第二种是 ...
- HDU 5831 Rikka with Parenthesis II (贪心) -2016杭电多校联合第8场
题目:传送门. 题意:T组数据,每组给定一个长度n,随后给定一个长度为n的字符串,字符串只包含'('或')',随后交换其中两个位置,必须交换一次也只能交换一次,问能否构成一个合法的括号匹配,就是()( ...
- HDU 5821 Ball (贪心排序) -2016杭电多校联合第8场
题目:传送门. 题意:T组数据,每组给定一个n一个m,在给定两个长度为n的数组a和b,再给定m次操作,每次给定l和r,每次可以把[l,r]的数进行任意调换位置,问能否在转换后使得a数组变成b数组. 题 ...
随机推荐
- FastJson反序列化1-FastJson基础使用及反序列化流程分析
1.FastJson简介及使用 fastjson是阿里巴巴的开源JSON解析库,它可以解析JSON格式的字符串,支持将Java Bean序列化为JSON字符串,也可以从JSON字符串反序列化到Java ...
- KingbaseES V8R6 中walminer的使用
前言 walminer工具可以帮助dba挖掘wal日志中的内容,看到某时间对应数据库中的具体操作.例如挖掘日志后可以看到数据库某时间有哪些dml语句. walminer的限制与约束 WalMiner工 ...
- archlinux 格式化分区并创建文件系统后,分区的文件系统没有改变
这就需要格式化分区并创建文件系统后 再执行partprobe应该就可以看到分区的文件系统改变了 partprobe partprobe命令用于通知操作系统重新读取分区表,以便识别新创建的分区或者删除的 ...
- #双指针#洛谷 7521 [省选联考 2021 B 卷] 取模
题目传送门 分析 将 \(a\) 排序后从大到小枚举 \(a_k\),注意枚举的时候重复的只考虑一次,那么可以将其它数按照模 \(a_k\) 后排序, 答案只可能来自最大值与次大值之和取模或者之和最接 ...
- 使用 GitLab CI/CD 和阿里云 CLI 自动部署前端项目
一.什么是 CI/CD? CI(持续交付)是功能迭代后自动构建.打包.校验代码格式.跑单测.单测覆盖率,常见的就是 Webpack.Rollup.ESLint等. CD(持续部署)是经过 CI 后,代 ...
- 使用OHOS SDK构建libjpeg-turbo
参照OHOS IDE和SDK的安装方法配置好开发环境. 从github下载源码. 执行如下命令: git clone --depth=1 https://github.com/libjpeg-turb ...
- Jenkins安装插件很慢的解决方法
修改 Jenkins / update / default.json 这个文件就可以了 修改内容 1. 把 " www.google.com " 改成 " h ...
- NL2SQL基础系列(1):业界顶尖排行榜、权威测评数据集及LLM大模型(Spider vs BIRD)全面对比优劣分析[Text2SQL、Text2DSL]
NL2SQL基础系列(1):业界顶尖排行榜.权威测评数据集及LLM大模型(Spider vs BIRD)全面对比优劣分析[Text2SQL.Text2DSL] Text-to-SQL(或者Text2S ...
- 推荐两款HTTP请求Mock利器
1.背景 在日常测试过程中或者研发开发过程中,目前接口暂时没有开发完成,测试人员又要提前介入接口测试中,测试人员不仅仅只是简单的编写测试用例,也可以通过一些mock的方法进行来提前根据接口测试的情况进 ...
- .NET Emit 入门教程:第六部分:IL 指令:8:详解 ILGenerator 指令方法:类型转换指令
前言: 经过前面几篇的学习,我们了解到指令的大概分类,如: 参数加载指令,该加载指令以 Ld 开头,将参数加载到栈中,以便于后续执行操作命令. 参数存储指令,其指令以 St 开头,将栈中的数据,存储到 ...
