字符串匹配算法：KMP

Knuth–Morris–Pratt（KMP）是由三位数学家克努斯、莫里斯、普拉特同时发现，所有人们用三个人的名字来称呼这种算法，KMP是一种改进的字符串匹配算法，它的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。它的时间复杂度是 O(m+n)

字符匹配：给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回  -1

在介绍KMP算法之前，我们先看一下另一种暴力算法（BF算法）去解字符匹配应该怎么做

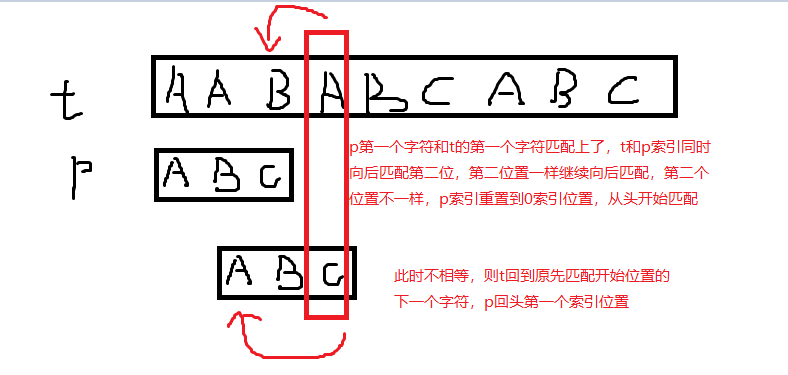
 BF算法：时间复杂度O(m*n)

class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        #hi是haystack的当前索引
        hi = 0
        haystackLength = len(haystack)
        needleLength = len(needle)
        for i in range(haystackLength - needleLength+1):
            #每次匹配等于和完整的needle的字符串逐一匹配
            if haystack[i:i+needleLength] == needle:
                return i
        return -1

KMP算法：时间复杂度O(m+n)

KMP构造了一个next列表来对应改位置索引如果匹配失败应该追溯回到什么位置，这样我们讲减少了匹配次数

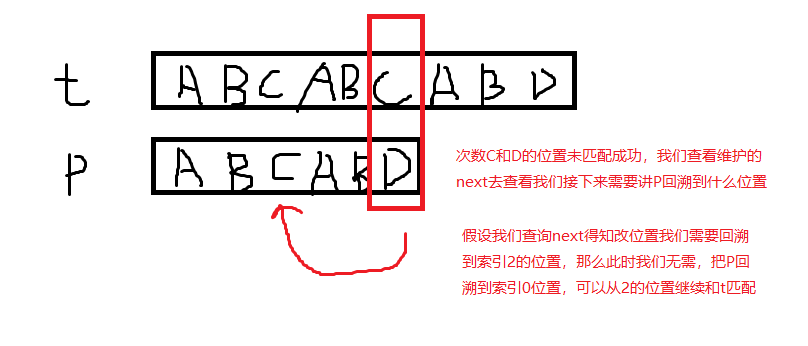
那么我们如何去构造维护我们的next（最长相同前后缀）

构造方法为：next[i] 对应的下标，为 P[0...i - 1] 的最长公共前缀后缀的长度，令 next[0] = -1。 具体解释如下：

例如对于字符串 abcba：
    前缀：它的前缀包括：a, ab, abc, abcb，不包括本身；
    后缀：它的后缀包括：bcba, cba, ba, a，不包括本身；
    最长公共前缀后缀：abcba 的前缀和后缀中只有 a 是公共部分，字符串 a 的长度为 1

我们通过动态规划来维护next，假设你知道next[0:i-1]位置上所有的回溯值，那么next[i-1]和next[i]相比仅仅多了一个位置，如果这个多的字符可以匹配上，那么next[i]一定等于next[i-1]+1(如下图所示)

那么如果匹配不上呢，匹配不上我们回溯到next[i-1]所需要回溯的位置，直到可以匹配上或到达无法追溯的位置next[0] = -1

    @staticmethod
    def same_start_end_str(p):
        """
        通过needle串来知道每个索引位置对应的最长前后缀
        例如ababa的最长前后缀是aba，前后缀是不和needle等长的最长相同前后缀
        """
        next = [-1] * (len(p)+1)
        si = -1
        ei = 0
        pl = len(p)
        while ei < pl :
            if si == -1 or p[si] == p[ei]:
                si += 1
                ei += 1
                next[ei] = si
            else:
                #无法匹配上，继续向前追溯
                si = next[si]

        return next

那我们有了next就可以取实现我们KMP算法了，完整代码如下

class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        next = self.same_start_end_str(needle)
        #hi是haystack当前索引,ni是needle当前索引
        hi = ni = 0
        hl = len(haystack)
        nl = len(needle)
        while hi < hl and ni < nl:
            if ni == -1 or haystack[hi] == needle[ni]:
                hi += 1
                ni += 1
            else:
                ni = next[ni]

        if ni == nl:
            return hi - ni
        else:
            return -1

    @staticmethod
    def same_start_end_str(p):
        """
        通过needle串来知道每个索引位置对应的最长前后缀
        例如ababa的最长前后缀是aba，前后缀是不和needle等长的最长相同前后缀
        """
        next = [-1] * (len(p)+1)
        si = -1
        ei = 0
        pl = len(p)
        while ei < pl :
            if si == -1 or p[si] == p[ei]:
                si += 1
                ei += 1
                next[ei] = si
            else:
                #无法匹配上，继续向前追溯
                si = next[si]

        return next