算法基础(一):串匹配问题(BF,KMP算法)

好家伙,学算法,

这篇看完,如果没有学会KMP算法,麻烦给我点踩

希望你能拿起纸和笔,一边阅读一边思考,看完这篇文章大概需要(20分钟的时间)

 

我们学这个算法是为了解决串匹配的问题

那什么是串匹配?

举个例子:

我要在"彭于晏吴彦祖"这段字符串中找到"吴彦祖"字符串

这就是串匹配

 

这两个算法太抽象了,我们直接做题吧

题目如下:

在A=“abcaaabaabaaac”中查找子串B=“aabaaa”，写出采用BF算法和KMP算法进行串匹配的全过程

 

1.BF(Brute Force,暴力)算法

暴力算法,我们从第一位开始进行匹配

　　1.1.若匹配成功,则匹配字符串"B"的下一位,

　　1.2.若匹配失败,则字符串"B"整体向右移动

　　直到匹配成功

匹配流程图:

第一次匹配:

 可以看见在进行第二个字符"a"的匹配时,匹配失败,字符串"B"整体右移

 

第二次匹配:

 

第三次匹配:(不想画图..)

第四次匹配:

 

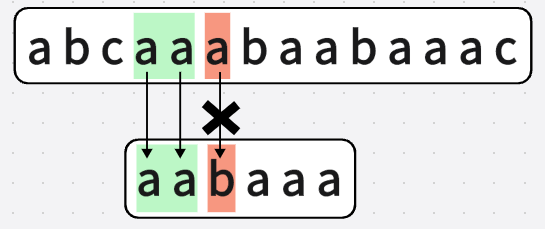
第五次匹配:

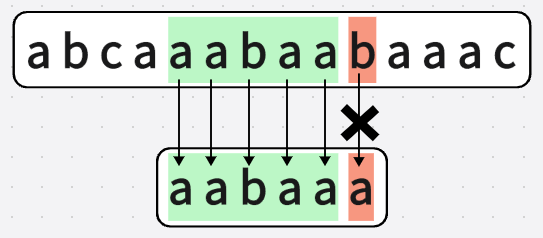
第六次匹配(不想画图....算了还是画吧):

 

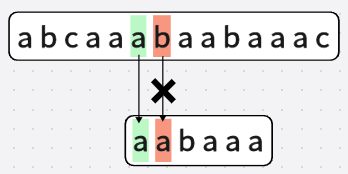
第七次匹配：

 

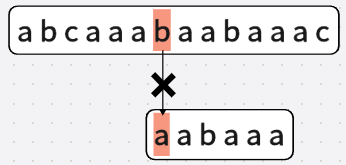
直到第八次:

直到全部字符串B全部匹配成功(又或者出现无法匹配的情况)

 

看看代码实现:

#include <stdio.h>
#include <string.h>

int find_substring(char *A, char *B) {
    int m = strlen(A); // A串长度
    int n = strlen(B); // B串长度
    int i, j;
    for (i = 0; i <= m - n; i++) { // i表示在A串中从第i开始查找子串B
        for (j = 0; j < n; j++) { // j表示在B串中与A串中的字符逐个比较
            if (A[i+j] != B[j]) // 不匹配则退出j循环
                break;
        }
        if (j == n) // 如果B串全部匹配，则返回A串中子串B第一次出现的位置
            return i;
    }
    return -1; // 如果没有匹配成功，则返回-1
}

int main() {
    char A[] = "abcaaabaabaaac";
    char B[] = "aabaaa";
    int index = find_substring(A, B);
    if (index >= 0)
        printf("子串B在A中第一次出现的位置是：%d\n", index);
    else
        printf("A中没有子串B\n");
    return 0;
}

嗯,看上去毫无技术含量

核心算法部分两个for循环写完了

 接下来进入本篇的主要内容

 

2.KMP(Knuth Morris Pratt算法)

这个算法是以人名命名的,那么,做好心理准备,这必然会有一定难度

 

2.1.我想偷懒(算法优化)

在前面BF算法的推演中,相信聪明的你一定察觉到了某些步骤看上去很多余

　　2.1.1.情况一

　　回到前面的推演

　　如果我们用"人"的思维去进行字符串匹配,会发现

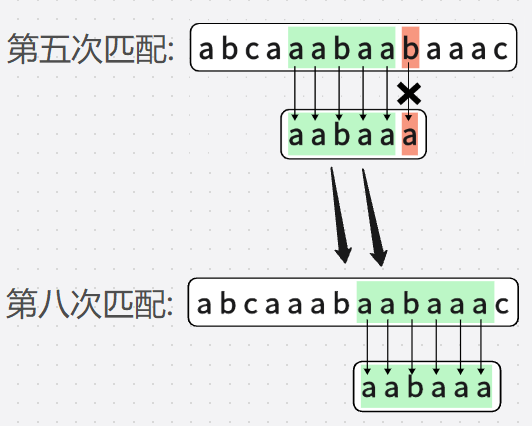
　　第六次匹配和第七次匹配完全是可以省略的,

　　我直接跳到"那个看上去正确"的位置

　　这么做是对的,可是这没有确切依据,凭借的是"直觉"

 

　　2.2.2.情况二

　　你也可能会有这样的想法:

　　我把已经配对过的字符全部跳过

     "将匹配过的字符都跳过 "   

　　于是,直接从第五次匹配跳到第十次匹配

　　直接跳到第十次匹配:

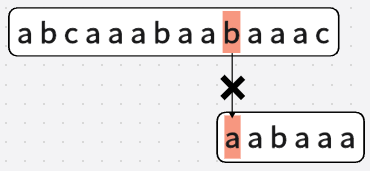
　　虽然达到了偷懒的目的,但错过了正确的答案

　　但你同样需要记住这个错误的情况

　　这有助于后续的理解

 

2.2.路标(部分匹配值表)

在前面,你知道,你不想达成情况二,你想要达成情况一

这时,你需要有个路标给你指示

(这或许是个不太好的比喻,

假设你现在吃坏肚子了,在某个大型的广场找厕所,你会怎么办?

我会抬头去找每个分岔路口的标识符,

你看见标识符了,在那边..)

这时候，我把我的字符串"B"的路标给你(后面会解释路标怎么来的)

部分匹配值表:

 

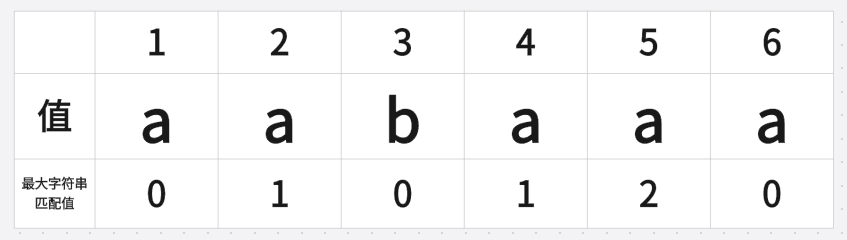
然后这个表该怎么用呢?

当匹配失败后,字符串"B"的移动位数P等于已匹配字符串数减去对应匹配值

比如说在第五次匹配中,

 

事实上,它移动的位数P = 已匹配字符串数  - 部分匹配值表对应匹配值

也就是 P = 5 - 2 = 3

而我们在推演中,也确实移动了3位

 

2.3.路标(部分匹配值表)的计算

这时候你开始疑问了?哥们,你这表怎么来的?

就两个字"规律"

看看这字符串吧"aabaaa"我们试图从中找出{已匹配字符串数}与{字符串B}的联系

"前缀"和"后缀"。 (1)"前缀"指除了最后一个字符以外，一个字符串的全部头部组合；

                            (2)"后缀"指除了第一个字符以外，一个字符串的全部尾部组合

"前缀"和"后缀"的最长的共有元素的长度

当{已匹配字符串数}为1,"a"的前缀为空,　　　　　　　　                后缀为空                                 共有元素长度为0

当{已匹配字符串数}为2,"aa"的前缀为[a]，　　　　　　　　           后缀为[a],                                共有元素长度为1

当{已匹配字符串数}为3,"aab"的前缀为[a,aa]，　　　　　　　　    后缀为[b,ab],                           共有元素长度为0

当{已匹配字符串数}为4,"aaba"的前缀为[a,aa,aab]，　　　　　　  后缀为[a,ba,aba],                    共有元素长度为1

当{已匹配字符串数}为5,"aabaa"的前缀为[a,aa,aab,aaba]，　　　  后缀为[a,aa,baa,abaa],           共有元素长度为2

当{已匹配字符串数}为6,"aabaaa"的前缀为[a,aa,aab,aaba,aabaa]，后缀为[a,aa,aaa,baaa,abaaa],共有元素长度为2,但是这已经无所谓,当匹配完成,部分匹配值表不再被需要

此时我们把共有元素填到表中,就得到了我们的"路标"表,当然了,他真正的名字是"部分匹配值表"

 

这时你会有两个疑问:

1.子串B=“aabaaa”的部分匹配值表为什么与A=“abcaaabaabaaac”是否有关?为什么?

答:无关

在KMP算法中计算子串B的部分匹配表时，我们只需要关注B本身，而不需要考虑B要在哪个字符串中进行匹配。

具体而言，部分匹配值的计算是通过B串本身的前缀和后缀来确定的，并不依赖于任何与B进行匹配的字符串的特定属性。

因此，子串B的部分匹配值表与A字符串中的字符内容和长度无关。可以在不考虑主串A的情况下，完全独立地计算出B的部分匹配值表。

2.为什么要如此麻烦地使用KMP算法,而不是使用更为方便地BF算法?

来吧,算法永远离不开的好朋友,时间复杂度O()

　　2.1.现在假设字符串A,B的长度分别为n,m

(1)BF算法

BF算法如此暴力,他的时间复杂度自然也很暴力,

不考虑最好最坏,平均的情况：在文本串和模式串的匹配字符数量较为相等的情况下，BF算法的时间复杂度为O(nm/2)，也就是O(nm)。

 

(2)KMP算法

考虑最好最坏情况

• 最好的情况：当文本串和模式串的匹配字符非常少时，KMP算法的时间复杂度为O(n)，其中n是文本串的长度。

• 最坏的情况：当文本串和模式串匹配字符非常多且不匹配时，KMP算法的时间复杂度为O(n+m)，其中n是文本串的长度，m是模式串的长度。

• 平均的情况：在文本串和模式串的匹配字符数量比较接近的情况下，KMP算法的时间复杂度为O(n+m)。

 

你看见了吗? nm和n+m,直接少了一个数量级,以人名命名的算法还是有点东西的

所以,结论:因为KMP算法的时间复杂度远低于BF算法,KMP算法更高效

 

好了你已经掌握了KMP算法思想的百分之七十了,其中最核心的部分匹配值表你已经掌握了

接下来的内容,是关于代码实现的

 

2.4.next()数组

这是便于代码实现和使用的{部分匹配值表}版本,它本质上还是部分匹配值表

既然是不同版本,那么它一定会遵循某些规则

部分匹配表为[ 0 1 0 1 2 0 ]，则对应的next数组为[ -1 0 1 0 1 2]。

具体操作:整体右移,然后首位赋值为-1

(1)第一步:整体右移

(2)第二步:首位赋值-1,

在KMP算法中，next数组的第一个元素next[0]的值必须为-1。

这是因为在算法中需要将待匹配串移动1个位置，如果next[0]的值为0，则下一次匹配就会跳过第一个字符，进入一个错误的状态。

而将next[0]设置为-1，则下一次匹配将从第一个字符开始，以正确的方式继续匹配。

又或者我们以另一种方式去理解:

第二种理解方式:

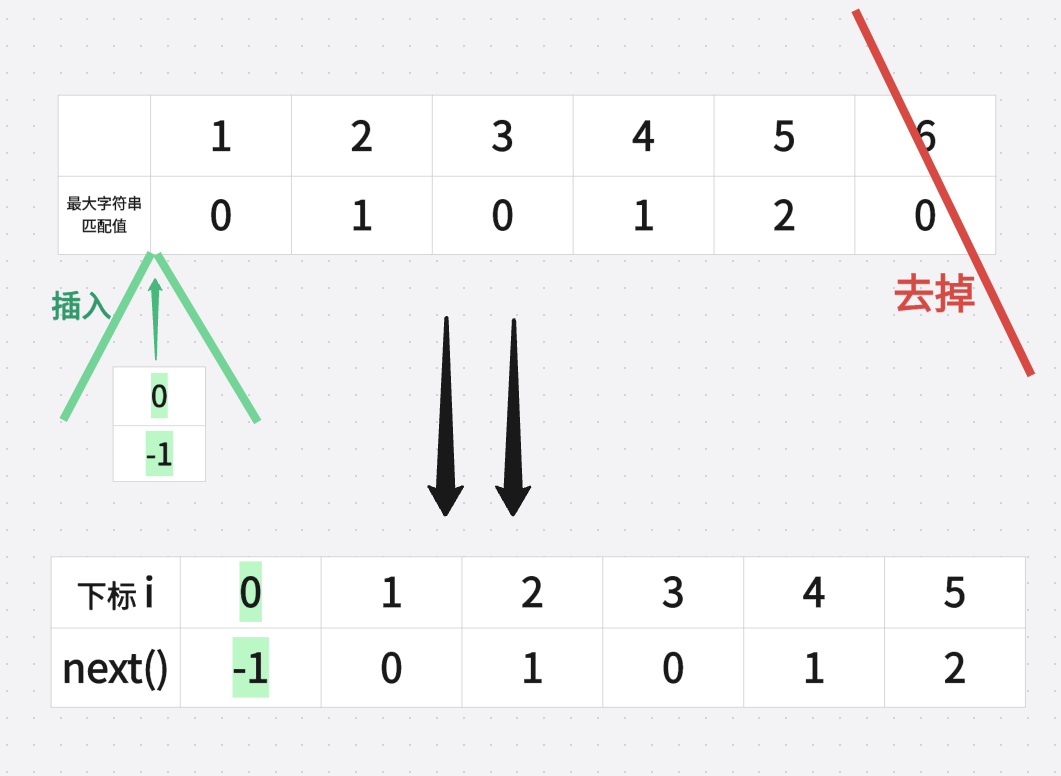
我们依旧使用那个方法去计算字符串匹配失败后移动的位数,移动位数P = 已配对字符串数 - next[i]

所以 如果一个字符都没配对,也就是匹配的字符串为0那么 移动位数 P = 已配对字符串数 - next[0] = 0 - (-1) = 1

　　 如果配对了5个字符,那么 移动位数 P = 已配对字符串数 - next[5] = 5 - 2 = 3

 如果还是理解不了,试着自己做题,或者上机试试

例题:A="aabbaabbaaabaac" B="aaabaa" 写出他的部分匹配表和next[]数组,并写出它匹配的过程

2.5.代码实现KMP算法

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void getNext(char* p, int* next, int n);

/* 在A中查找子串B的位置 */
int kmp_search(char* A, int n, char* B, int m)
{
    int i = 0, j = 0;
    int *next = (int*)malloc(sizeof(int) * m); // 申请next数组
    getNext(B, next, m); // 计算B串的next数组

    while (i < n && j < m) { // 从头到尾扫描A串和B串
        if (j == -1 || A[i] == B[j]) { // 匹配成功或者失配
            i++;
            j++;
        } else {
            j = next[j]; // 失配时根据next数组调整j的位置
        }
    }
    free(next); // 释放申请的空间
    if (j == m) { // 匹配成功
        return i - m;
    } else { // 匹配失败
        return -1;
    }
}

/* 计算模式串的next数组 */
void getNext(char* p, int* next, int n)
{
    int j = 0, k = -1;
    next[0] = -1; // next数组的第一个值为-1

    while (j < n - 1) { // 计算next数组
        if (k == -1 || p[j] == p[k]) { // 相等情况
            j++;
            k++;
            next[j] = k;
        } else {
            k = next[k]; // 不相等情况，回溯(k指针回溯)
        }
    }
}

int main()
{
    char A[] = "abcaaabaabaaac";
    char B[] = "aabaaa";
    int lenA = strlen(A); // 计算A的长度
    int lenB = strlen(B); // 计算B的长度

    int pos = kmp_search(A, lenA, B, lenB); // 在A中查找B的位置

    if (pos == -1) {
        printf("在A中没找到B!\n");
    } else {
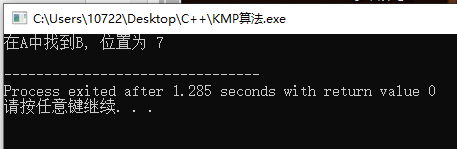
        printf("在A中找到B, 位置为 %d\n", pos);
    }

    return 0;
}