P1585 魔法阵 题解

题意：

题目传送门

可以看做一个人手中有一些宝石，并将宝石分成两组，一组的编号为 1 至 n×m/2，二组为 n×m/2+1 至 n×m+1。当两组两个宝石编号相差为 n×m/2 为一对。现在要遍历一个 n×m 的方阵，只能走上下左右，且每个格子必须且仅能到过 1 次。并在遍历同时对每一个格子放入宝石。即遍历的第 i 个格子放入编号为 i 的宝石。

对于一对宝石，如果第一组的宝石在第 x1 行第 y1 列，第二组宝石的在第 x2 行第 y2 列，则称它们的分值为 k1×abs(x1-x2)+k2×abs(y1-y2)。

现在要找出一种遍历顺序，使分值最大一对宝石分值最小，输出这个最小的最大分值。

思路:

看到是遍历，且数据范围非常小，考虑用 dfs。不过如果不加剪枝优化的爆搜，肯定会 TLE 飞，因此考虑剪枝。

首先是一个很好想的最优化剪枝：如果当前记录的最大值已经比之前的方案大了，那就不可能更新答案，没必要搜索，直接

返回。

但只有这一个剪枝还不行，我们发现题目中一个很重要的事：每个格子必须且仅能到过 1 次。因此当发现已经不可能满足要求的时候，便可以直接返回。

那如何判断呢？

当一个现在这个点的上下走过且左右没走，或者左右走过上下没走，则不能满足要求。

因为当上下走过时，他们所联通的路线一定将左右分别能到达的点分隔成两个连通块，左右走过上下没走也是同理。

画个图方便理解一下：

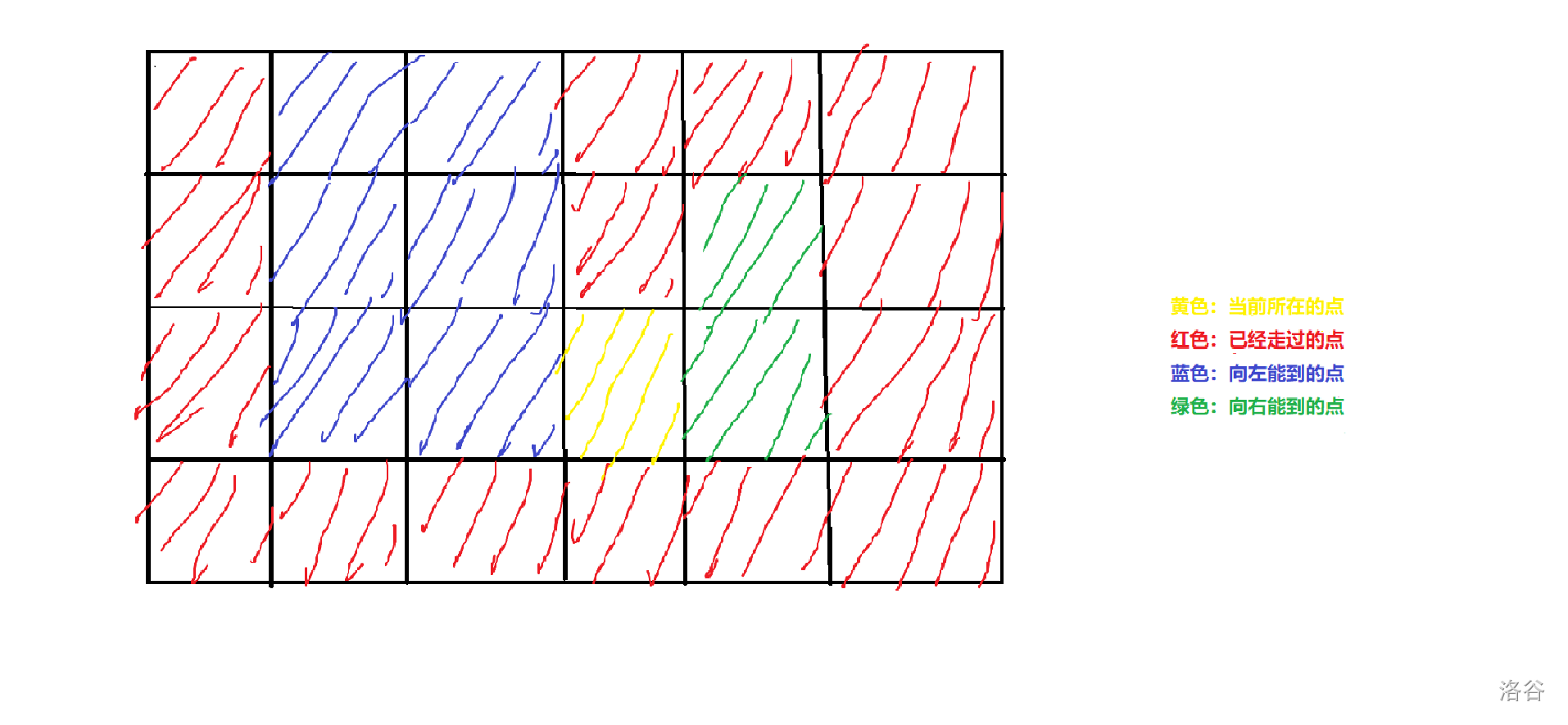
有了这些就可以愉快的写代码了。

代码：

请勿抄袭。

#include<bits/stdc++.h>
using namespace std;
int n,m,k1,k2;
//与题目中意义一致
int ans=1e10;//记录答案
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1}; //移动的方向数组
bool f[61][61];//记录是否被走过
int q[2500][2];//记录第一组宝石所在的点
inline void dfs(int x,int y,int p,int mmax)
//x,y：当前点的坐标，p：搜到的宝石编号，mmax:目前的最大的分数
{
	if(mmax>=ans) return;//最优性剪枝
	if(f[x+1][y]&&f[x-1][y]&&!f[x][y+1]&&!f[x][y-1]) return;
	if(f[x][y+1]&&f[x][y-1]&&!f[x+1][y]&&!f[x-1][y]) return;
	//两种不可能完成遍历的情况
	if(p<=n*m/2) q[p][0]=x,q[p][1]=y;//第一组，直接存储
	else//第二组，开始计算
	{
		mmax=max(mmax,(k1*abs(x-q[p-(n*m/2)][0])+k2*abs(y-q[p-(n*m/2)][1])));//根据公式求值
	}
	if(p==n*m)//搜索完了
	{
		if(mmax<ans) ans=mmax;//能更新答案则更新
		return;
	}
	for(int i=0;i<4;i++)//继续向能走到的点搜索
	{
		int xx=x+dx[i];
		int yy=y+dy[i];
		if(!f[xx][yy])//没走过，可以走
		{
			f[xx][yy]=1;//标记
			dfs(xx,yy,p+1,mmax);
			f[xx][yy]=0;//回溯
		}
	}
}
int main()
{
	scanf("%d%d%d%d",&n,&m,&k1,&k2);
	for(int i=0;i<=n+1;i++) f[i][0]=1,f[i][m+1]=1;
	for(int i=0;i<=m+1;i++) f[0][i]=1,f[n+1][i]=1;
	//上面两个循环是边界处理，因为不能走出方阵，所以将边界设为1，防止出界
	f[1][1]=1;
	dfs(1,1,1,0);//从1,1点开始搜索
	printf("%d\n",ans);//输出
	return 0;
}

写题解不易，点个赞呗。