2021-04-30：一条直线上有居民点，邮局只能建在居民点上。给定一个有序正数数组arr，每个值表示 居民点的一维坐标，再给定一个正数 num，表示邮局数量。选择num个居民点建立num个 邮局，使

2021-04-30：一条直线上有居民点，邮局只能建在居民点上。给定一个有序正数数组arr，每个值表示 居民点的一维坐标，再给定一个正数 num，表示邮局数量。选择num个居民点建立num个 邮局，使所有的居民点到最近邮局的总距离最短，返回最短的总距离。【举例】arr=[1,2,3,4,5,1000]，num=2。第一个邮局建立在 3 位置，第二个邮局建立在 1000 位置。那么 1 位置到邮局的距离 为 2， 2 位置到邮局距离为 1，3 位置到邮局的距离为 0，4 位置到邮局的距离为 1， 5 位置到邮局的距 离为 2，1000 位置到邮局的距离为 0。这种方案下的总距离为 6， 其他任何方案的总距离都不会 比该方案的总距离更短，所以返回6。

福大大 答案2021-04-30：

动态规划。

代码用golang编写。代码如下：

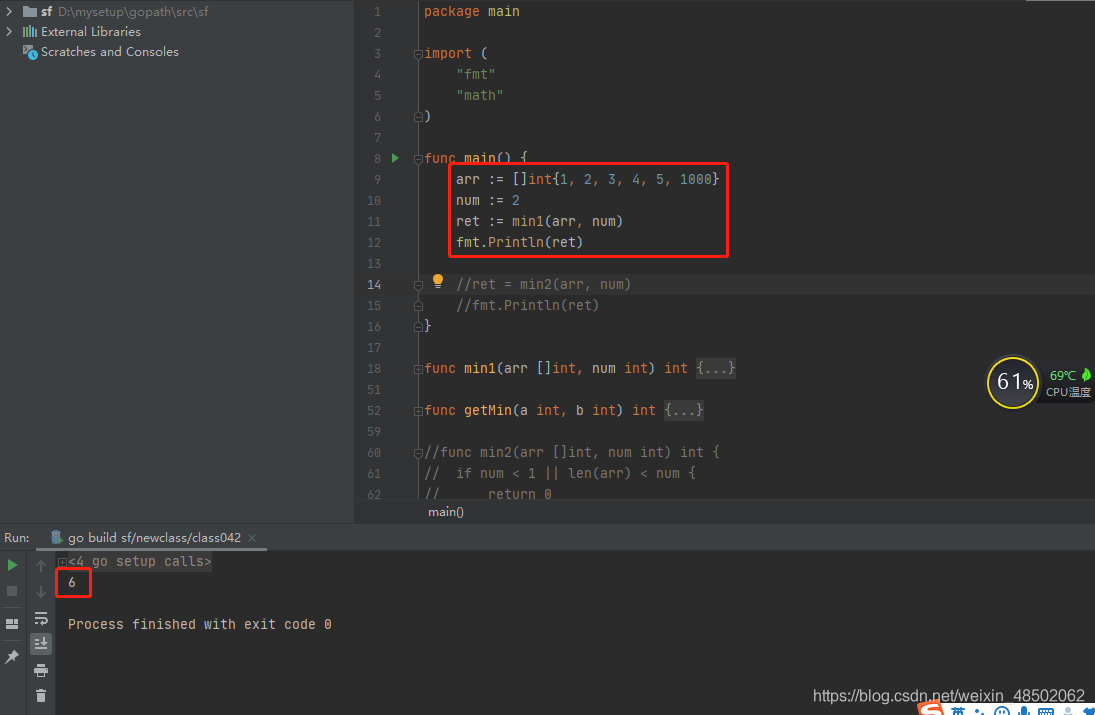
package main

import (
    "fmt"
    "math"
)

func main() {
    arr := []int{1, 2, 3, 4, 5, 1000}
    num := 2
    ret := min1(arr, num)
    fmt.Println(ret)

    //ret = min2(arr, num)
    //fmt.Println(ret)
}

func min1(arr []int, num int) int {
    if num < 1 || len(arr) < num {
        return 0
    }
    N := len(arr)
    w := make([][]int, N+1)
    for i := 0; i < N+1; i++ {
        w[i] = make([]int, N+1)
    }
    for L := 0; L < N; L++ {
        for R := L + 1; R < N; R++ {
            w[L][R] = w[L][R-1] + arr[R] - arr[(L+R)>>1]
        }
    }

    dp := make([][]int, N)
    for i := 0; i < N; i++ {
        dp[i] = make([]int, num+1)
    }
    for i := 0; i < N; i++ {
        dp[i][1] = w[0][i]
    }
    for i := 1; i < N; i++ {
        for j := 2; j <= getMin(i, num); j++ {
            ans := math.MaxInt32
            for k := 0; k <= i; k++ {
                ans = getMin(ans, dp[k][j-1]+w[k+1][i])
            }
            dp[i][j] = ans
        }
    }
    return dp[N-1][num]
}

func getMin(a int, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

//func min2(arr []int, num int) int {
//  if num < 1 || len(arr) < num {
//      return 0
//  }
//  N := len(arr)
//  w := make([][]int, N+1)
//  for i := 0; i < N+1; i++ {
//      w[i] = make([]int, N+1)
//  }
//  for L := 0; L < N; L++ {
//      for R := L + 1; R < N; R++ {
//          w[L][R] = w[L][R-1] + arr[R] - arr[(L+R)>>1]
//      }
//  }
//
//  dp := make([][]int, N)
//  for i := 0; i < N; i++ {
//      dp[i] = make([]int, num+1)
//  }
//
//  best := make([][]int, N)
//  for i := 0; i < N; i++ {
//      best[i] = make([]int, num+1)
//  }
//  for i := 0; i < N; i++ {
//      dp[i][1] = w[0][i]
//      best[i][1] = -1
//  }
//  for j := 2; j <= num; j++ {
//      for i := N - 1; i >= j; i-- {
//          down := best[i][j-1]
//          up := twoSelectOne(i == N-1, N-1, best[i+1][j])
//          ans := math.MaxInt32
//          bestChoose := -1
//          for leftEnd := down; leftEnd <= up; leftEnd++ {
//              leftCost := twoSelectOne(leftEnd == -1, 0, dp[leftEnd][j-1])
//              rightCost := twoSelectOne(leftEnd == i, 0, w[leftEnd+1][i])
//              cur := leftCost + rightCost
//              if cur <= ans {
//                  ans = cur
//                  bestChoose = leftEnd
//              }
//          }
//          dp[i][j] = ans
//          best[i][j] = bestChoose
//      }
//  }
//  return dp[N-1][num]
//}

func twoSelectOne(isSelectFirst bool, a int, b int) int {
    if isSelectFirst {
        return a
    } else {
        return b
    }
}

执行结果如下：

---

左神java代码