2018/1/28 每日一学 单源最短路的SPFA算法以及其他三大最短路算法比较总结

刚刚AC的pj普及组第四题就是一种单源最短路。

我们知道当一个图存在负权边时像Dijkstra等算法便无法实现；

而Bellman-Ford算法的复杂度又过高O(V*E），SPFA算法便派上用场了。

其实SPFA 是用队列的优化，过程详见下图（PS:图片转自网络）

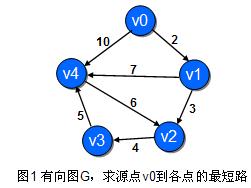
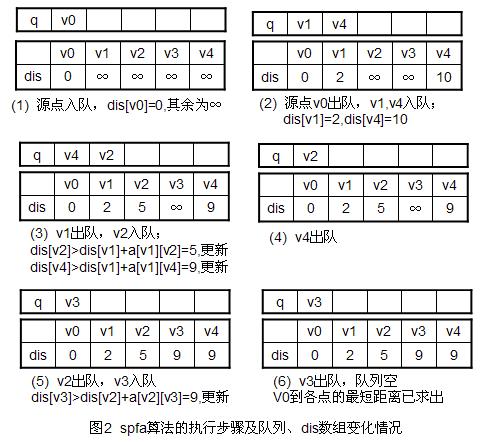
好了，以上图片基本已经说明的SPFA的过程，下面就是代码实现：

模板如下：

void spfa(){
    ; i<=n; i++) dis[i]=INF; //初始化
    dis[start]=; inq[start]=;
    q.push(start);
    int i, v;
    while (!q.empty){
        v=q.front(); // 取队首节点
        q.pop();
        inq[v]=;   //释放节点，因为这节点可能下次被其他节点松弛,重新入队
        ; i<=n; i++)  //枚举所有顶点
            && dis[i]>dis[v]+a[v][i]){  //判断
                dis[i] = dis[v]+a[v][i];   //修改
                if (!inq[i]){ // 如果扩展结点i不在队列中，入队
                    q.push(i);
                    vis[i]=;
                }
           }
    }
}

可以看到，因为维护队列，和bfs有其曲同工之妙，但有一点不同！！！

bfs一旦入队，哪怕后面出队也无法在入队，而SPFA不同。

从数组名vis[i](BFS),inq[i](SPFA)可以看出定义不同。

那么对于有负权边，SPFA时间会大大增加……

不难想到DFS会不会快一点（好吧，既然都说了，肯定快，233）。

大约是O（E）。

代码如下：

void spfa(now){//DFS
    ; i<=edge[now]; i++)  //枚举从顶点now发出的边
       if (dis[to[now][i]>dis[now]+a[now][to[now][i]]){
        dis[to[now][i]=dis[now]+a[now][to[now][i]];
        spfa(to[now][i]);//继续DFS
       }
}

我们知道DFS其实是遍历到终点才换成另一条路，因此可以用来判断负权边！！

只需判断是否回到之前的节点即可，可以用 vis[i]  bool数组记录。

再看看Bellman-Ford算法，思路太简单，枚举点和边，就是时间比较长，为O(VE）。

代码如下：（转自百度百科）

#include<iostream>
#include<cstdio>
using namespace std;  

#define MAX 0x3f3f3f3f
#define N 1010
int nodenum, edgenum, original; //点，边，起点  

typedef struct Edge //边
{
    int u, v;
    int cost;
}Edge;  

Edge edge[N];
int dis[N], pre[N];  

bool Bellman_Ford()
{
    ; i <= nodenum; ++i) //初始化
        dis[i] = (i == original ?  : MAX);
    ; i <= nodenum - ; ++i)
        ; j <= edgenum; ++j)
            if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛（顺序一定不能反~）
            {
                dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;
                pre[edge[j].v] = edge[j].u;
            }
            ; //判断是否含有负权回路
            ; i <= edgenum; ++i)
                if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost)
                {
                    flag = ;
                    break;
                }
                return flag;
}  

void print_path(int root) //打印最短路的路径（反向）
{
    while(root != pre[root]) //前驱
    {
        printf("%d-->", root);
        root = pre[root];
    }
    if(root == pre[root])
        printf("%d\n", root);
}  

int main()
{
    scanf("%d%d%d", &nodenum, &edgenum, &original);
    pre[original] = original;
    ; i <= edgenum; ++i)
    {
        scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost);
    }
    if(Bellman_Ford())
        ; i <= nodenum; ++i) //每个点最短路
        {
            printf("%d\n", dis[i]);
            printf("Path:");
            print_path(i);
        }
    else
        printf("have negative circle\n");
    ;
}  

看到核心部分，不难想到外层i跟内层循环无关，因此可以优化，即如果内层无松弛，可以提前结束！

这样一来，速度还是可以的……

之后我们看看dijkstra算法，其实就是贪心。

dis数组用来储存起始点到其他点的最短路。

转移方程为：

dis[i]=min(dis[i],dis[j]+w[j][i]|j为i能到达的点)

一开始dis[i]=INF,dis[start]=0;

很显然，不能处理有负边的情况……

时间为（V^2）.两层循环解决。

注意每次选用没更新过的离源点最近的点对外拓展。

代码如下：

#include<stdio.h>
#include<stdlib.h>
#define INF 1<<28
#define N 1000+5
int a[N][N];
int d[N];
bool vis[N];
int i,j,k;
int m;//m代表边数
int n;//n代表点数
int main()
{
scanf("%d%d",&n,&m);
int mn;
int x,y,z;
;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
a[x][y]=a[y][x]=z;
}
;i<=n;i++)
d[i]=INF;
;i<=m;i++)
{
mn=INF;
;j<=n;j++)
if(!vis[j]&&d[j]<mn)
{
mn=d[j];
k=j;
}
vis[k]=;
;j<=n;j++)
&&d[j]>d[k]+a[k][j])
d[j]=d[k]+a[k][j];
}
;i<=n;i++)
printf("%d ",d[i]);
;
}

最后用最最最最……最智障的floyd算法结束今天学习（完全是为了凑齐四种算法，基本没啥可说）

直接看核心代码

; k<=n; k++)
 ; i<=n; i++)
 ; j<=n; j++)
 {
 if(w[i][j]>w[i][k]+w[k][j])
 w[i][j]=map1[i][k]+w[k][j];
 } 

注意最外层是循环中间的点！！！

其他就比较简单，不解释了，ok!