java实现最小生成树的prim算法和kruskal算法

在边赋权图中，权值总和最小的生成树称为最小生成树。构造最小生成树有两种算法，分别是prim算法和kruskal算法。在边赋权图中，如下图所示:

　　

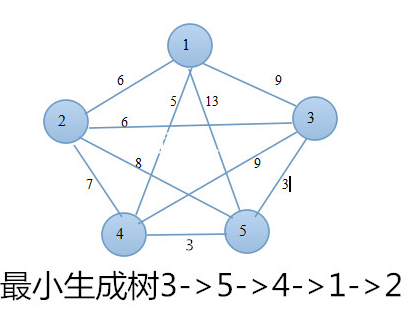
在上述赋权图中，可以看到图的顶点编号和顶点之间邻接边的权值，若要以上图来构建最小生成树。结果应该如下所示:

　　

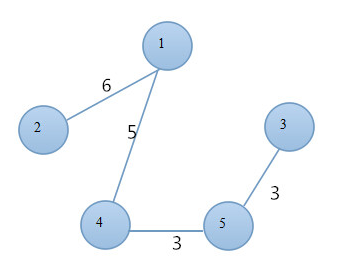
这样构建的最小生成树的权值总和最小，为17

在构建最小生成树中，一般有两种算法，prim算法和kruskal算法

在prim算法中，通过加入最小邻接边的方法来建立最小生成树算法。首先构造一个零图，在选一个初始顶点加入到新集合中，然后分别在原先的顶点集合中抽取一个顶点，使得构成的边为权值最小，然后将该笔边加入到图中，并将抽出的顶点加入到新集合中，重复这个过程，知道新集合等于原先的集合。

代码一：（java）

 /**
  * 最小生成树的prim算法
  * @author liuy
  */
 public class Prim {

     public static void prim(int num, float[][] weight) {  //num为顶点数，weight为权
         float[] lowcost = new float[num + 1];  //到新集合的最小权

         int[] closest = new int[num + 1];  //代表与s集合相连的最小权边的点

         boolean[] s = new boolean[num + 1];  //s[i] == true代表i点在s集合中

         s[1] = true;  //将第一个点放入s集合

         for(int i = 2; i <= num; i++) {  //初始化辅助数组
             lowcost[i] = weight[1][i];
             closest[i] = 1;
             s[i] = false;
         }

         for(int i = 1; i < num; i++) {
             float min = Float.MAX_VALUE;
             int j = 1;
             for(int k = 2; k <= num; k++) {
                 if((lowcost[k] < min) && (!s[k])) {//根据最小权加入新点
                     min = lowcost[k];
                     j = k;
                 }
             }

             System.out.println("加入点" + j + ". " + j + "---" + closest[j]);//新加入点的j和与j相连的点

             s[j] = true;//加入新点j

             for(int k = 2; k <= num; k++) {
                 if((weight[j][k] < lowcost[k]) && !s[k]) {//根据新加入的点j,求得最小权
                     lowcost[k] = weight[j][k];
                     closest[k] = j;
                 }
             }
         }
     }

     public static void main(String[] args) {
         //              ①
         //            /  |  /
         //           6   1   5
         //          /    |    /
         //        ②-5--③--5--④
         //         /    //    /
         //          3  6  4  2
         //           //    //
         //           ⑤--6-⑥
         //最小生成树为：
         //              ①
         //               |
         //               1
         //               |
         //        ②-5--③        ④
         //         /     /    /
         //          3     4  2
         //           /     //
         //           ⑤        ⑥
         //
         float m = Float.MAX_VALUE;
         float[][] weight = {{0, 0, 0, 0, 0, 0, 0},
                             {0, m, 6, 1, 5, m, m},
                             {0, 6, m, 5, m, 3, m},
                             {0, 1, 5, m, 5, 6, 4},
                             {0, 5, m, 5, m, m, 2},
                             {0, m, 3, 6, m, m, 6},
                             {0, m, m, 4, 2, 6, m}};//上图的矩阵
         prim(weight.length - 1, weight);
         //加入点3. 3---1
         //加入点6. 6---3
         //加入点4. 4---6
         //加入点2. 2---3
         //加入点5. 5---2
     }
 }

代码二：（java）

 package 最小生成树;
 /*
  * 最小生成树prim算法，加入最小邻接边生成最小生成树。
  * 首先构造一个零图，选择一个初始点加入到集合中，
  * 然后分别从原来顶点的集合中抽取一个顶点，
  * 选择的标准是构造成的树的权值最小，
  * 循序渐进最终生成一棵最小生成树
  */
 public class prim {

  /*
   * m:定义为无法到达的距离
   * weight:邻接矩阵表,weight表示权值
   * verNum:顶点的个数
   * lowerW:到新集合的最小权值
   * edge:存储到新集合的边
   * checked:判定顶点是否被抽取的集合
   */

  static int m=Integer.MAX_VALUE;
  static int[][] weight={
    {0, 0, 0, 0, 0, 0},
    {0, m, 6, 9, 5, 13},
    {0, 6, m, 6,7,8},
    {0, 9,6,m,9,3},
    {0, 5,7,9,m,3},
    {0,13,8,3,3,m}
  };
  static int verNum=weight.length;
  static int []lowerW=new int[verNum];
  static int []edge=new int[verNum];
  static boolean []checked=new boolean[verNum];

  public void prim(int n,int [][]w){
   checked[1]=true;            //抽取第一个顶点

   for(int i=1;i<=n;i++){          //初始化顶点集合
    lowerW[i]=w[1][i];
    edge[i]=1;
    checked[i]=false;
   }

   for(int i=1;i<=n;i++){
    int min=Integer.MAX_VALUE;
    int j=1;
    for(int k=2;k<=n;k++){        //判定是否抽取该顶点
     if(lowerW[k]<min&&(!checked[k])){
      min=lowerW[k];
      j=k;
     }
    }
    if(i<n)                //避免输出第一个顶点到第一个顶点的情况
    System.out.println(j+"-->"+edge[j]);

    checked[j]=true;           //将顶点加入到新集合中

    for(int k=2;k<=n;k++){        //根据新加入的顶点，求得最小的权值
     if((w[j][k]<lowerW[k])&&(!checked[k])){
      lowerW[k]=weight[j][k];
      edge[k]=j;
     }
    }
   }
  }

  public static void main(String[] args) {
   // TODO Auto-generated method stub
   prim p=new prim();
   p.prim(verNum-1,weight);
  }
 }

在kruskal算法中，根据边的权值以递增的方式逐渐建立最小生成树。具体操作是:将赋权图每个顶点都看做森林，然后将图中每条邻接边的权值按照升序的方式进行排列，接着从排列好的邻接边表中抽取权值最小的边，写入该边的起始顶点和结束顶点，连接顶点将森林构成树，然后读取起始结束顶点的邻接边，优先抽取权值小的邻接边，继续连接顶点将森林构成树。添加邻接边的要求是加入到图中的邻接边不构成回路。如此反复进行，直到已经添加n-1条边为止。

代码一：（java）

 package 最小生成树;
 import java.util.ArrayList;
 import java.util.Scanner;
 /*
  * 最小生成树kruskal算法：首先将每个顶点作为一棵森林，升序比较该顶点的邻接边，
  * 每次取最小权值的邻接边，将该邻接边连接的顶点与原先顶点构成一棵树，接着寻找
  * 下一个顶点，继续按照邻接边权值升序进行比较，取权值最小的构成树...
  *
  * 该类用一个Edge类构成一个邻接边的信息，包括邻接边的起始顶点与结束顶点，权值。
  * 用类Edge创建对象，录入对象信息，按照对象的权值进行比较，符合条件的对象加入
  * 到链表中，最终按照链表顺序输出最小生成树。
  */
 public class kruskal {

  /*
   * Max:定义顶点数组的最大值
   * edge:链表edge，存储构造的Edge对象
   * target:链表trget,存储最终得到结果的Edge对象
   * parent:存储顶点信息的数组
   * n:顶点数
   */
  int Max=100;
  ArrayList<Edge>edge=new ArrayList<Edge>();
  ArrayList<Edge>target=new ArrayList<Edge>();
  int[] parent=new int[Max];
  Float TheMax=Float.MAX_VALUE;
  int n;

  public void init(){
   /**
    * p:起始顶点
    * q:结束顶点
    * w:边的权值
    * n:顶点个数
    */
   Scanner scan =new Scanner(System.in);
   int p,q;
   double w;
   System.out.println("请输入结点的个数:");
   n=scan.nextInt();
   System.out.println("按照'A,B,C'的格式输入边与边的信息,ABC分别代表边的起始顶点，结束顶点，权值(输入-1 -1 -1结束输入):");
   while(true){
    p=scan.nextInt();
    q=scan.nextInt();
    w=scan.nextDouble();
    if(p<0||q<0||w<0)break;
    Edge e=new Edge();
    e.start=p;
    e.end=q;
    e.weight=w;
    edge.add(e);
   }
   for(int i=1;i<=n;++i){          //初始化边的信息数组
    parent[i]=i;
   }
  }

  /*
   * 对象合并，将上一对象的结束边作为下一对象的起始边
   */
  public void union(int j,int k){
   for(int i=1;i<=n;++i){
    if(parent[i]==j)
     parent[i]=k;
   }
  }

  public void kruskal(){
   int i=0;                 //顶点
   while(i<n-1&&edge.size()>0){       //如果只有一条边或者没有边跳出
    double min=Double.MAX_VALUE;
    Edge temp=null;
    for(int j=0;j<edge.size();++j){      //遍历图形
     Edge tt=edge.get(j);
     if(tt.weight<min){           //若两个顶点有权值，即相连
     min=tt.weight;
     temp=tt;
     }
   }

   //构造一棵树
   int jj=parent[temp.start];
   int kk=parent[temp.end];

   if(jj!=kk){
    ++i;                 //以end作为下一条边的start,寻找下一条边
    target.add(temp);           //将找到的边放入目标集合中
    union(jj,kk);
   }
   edge.remove(temp);           //将临时边删除
   }
   System.out.println("最小生成树的路径是:");
   for(int k=0;k<target.size();++k){     //输出最小生成树
    Edge e=target.get(k);
    System.out.println(e.start+"-->"+e.end);
   }
  }

  public static void main(String[] args) {
   // TODO Auto-generated method stub
    kruskal kr=new  kruskal();
    kr.init();
    kr.kruskal();
  }
 }
 /*
  * start:起始顶点
  * end:结束顶点
  * weight:权值
  */
 class Edge{
  public int start;
  public int end;
  public double weight;
 }