第二次作业——个人项目实战（Sudoku)

Github:Sudoku

项目相关要求

利用程序随机构造出N个已解答的数独棋盘 。

输入

数独棋盘题目个数N

输出

随机生成N个 不重复 的 已解答完毕的 数独棋盘，并输出到sudoku.txt中，输出格式见下输出示例。

输入示例

sudoku.exe -c 1

输出示例

6 1 2 3 4 5 7 9 8
3 4 5 7 9 8 6 1 2
7 9 8 6 1 2 3 4 5
2 6 1 5 3 4 8 7 9
8 7 9 2 6 1 5 3 4
5 3 4 8 7 9 2 6 1
1 2 6 4 5 3 9 8 7
9 8 7 1 2 6 4 5 3
4 5 3 9 8 7 1 2 6

---

遇到的困难及解决方法

一、第一次使用VS

• 困难描述： 第一次使用VS，程序构建流程不清除，包括如何添加单元测试，将lib与主程序分开。
• 做过哪些尝试： 从github下载gtest的解决方案查看配置，换过无数次VS版本。
• 收获： VS各个版本的功能有所不同, VS compare,最终选择Visual Studio Enterprise 2015

二、单元测试&覆盖率

• 困难描述： VS除了Enterprise版本其他没有覆盖率分析。
• 做过哪些尝试： 使用其他扩展，但没找到一个扩展可以分析VS所托管的单元测试。
• 收获： 切回Visual Studio Enterprise 2015， 成功分析覆盖率

三、持续集成

• 困难描述： 想通过TravisCi和Coveralls+Github进行持续集成和单元测试覆盖率分析，当我push代码(source)之后，Travis 配置 持续集成，单元测试通过之后，自动构建项目，并发布到github，然后coveralls进行单元测试覆盖率分析。
• 做过哪些尝试： 各种Google，猜想：如果需要配置持续集成，必须使用gtest等VS以外的单元测试框架，于是放弃。

---

设计说明

解题思路

阅读题目后，首先想到的是爆搜，所有的情况有\((9!)^9\) , 仔细分析数独的特点，每一行每一列的数都是1-9 ,并且划分为9个区域，每个区域的3*3方格都是 1-9 ,那么，我们很容易可以确定前3行，先确定第一行的数，第2， 3行再通过偏移得出来，最后得到满足条件的前3行。 得到满足的前3行， 可以通过前三行分块列变换得到后6行，最后得出数独解矩阵。

具体的解法

设计实现

目录结构：

├─BIN
│      checker.exe
│      checker.iobj
│      checker.ipdb
│      checker.pdb
│      lib.lib
│      Sudoku.exe
│      Sudoku.iobj
│      Sudoku.ipdb
│      Sudoku.pdb
│      Sudoku.txt
│
└─Sudoku
    │  Sudoku.sln
    │
    ├─checker
    │  │  main.cpp
    │
    ├─lib
    │  │  check.cpp
    │  │  check.h
    │  │  generator.cpp
    │  │  generator.h
    │
    └─Sudoku
        │  main.cpp

lib：check的方法有：

bool checkdiff(int arr[], int size); // 检查数组的元素是否互异，并且是1-size的自然数
bool checkSudoku(int grid[10][10]); // 检查该grid是否为合法的数独解
int string2Int (string s); // 将string转为int类型，用于命令行输入参数的转换

lib：generator

class generator
{
	public:
		generator(int sn); // 构造函数，参数sn: 左上角第一个数，并生成第一行满足条件的全排列
    	int(*generateGrid(int topLine[]))[10][10]; // 生成数独解 topLine： 第一行的排列
    	void generate(int n); // 打印n个数独解
    	void printGrid(int Grid[10][10]);
    	int(*firstLine)[10]; // 第一行
};

generator(6) -> generate(n) -> generateGrid(topLine);

---

代码说明

generator::generator(int sn) {
  firstLine = new int[50000][10];
  int line[10];
  int cnt = 0;
  line[cnt ++ ] = sn;
  for (int i = 1; i <= 9; i++) {
    if (i != sn) line[cnt++] = i;
  }
  int tot = 0;
  while (next_permutation(line + 1, line + 9)) {
    for (int i = 0; i < 9; i++) firstLine[tot][i] = line[i];
    tot++;
  }
}
// next_permutation 生成下一个全排列，返回true/false
// 预期复杂度 O(9!)
// 需生成至少4*1e4个排列。8! > 4*1e4,满足需求。

 int (*generator::generateGrid(int topLine[]))[10][10] {
  int (*result)[10][10] = new int [40][10][10];
  int grid[10][10];
  for (int i = 0; i < 9; i++)grid[0][i] = topLine[i];
  for (int i = 1; i < 3; i++) {
    for (int j = 0; j < 9; j++) {
     grid[i][j] = grid[i - 1][(j + 3) % 9];
    }
  } // 生成前3行
  for (int i = 3; i < 9; i++) {
    for (int j = 0; j < 9; j++) {
      grid[i][j] = grid[i - 3][(j % 3 == 0 ? j + 2 : j - 1)];
    }
  } // 生成4 - 9 行
  int order[10] = { 0, 1, 2, 3, 4, 5, 6, 7, 8 };
  int tot = 0;
  while (next_permutation(order + 3, order + 6)) {
    while (next_permutation(order + 6, order + 9)) {
      for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
          result[tot][i][j] = grid[order[i]][j];
        }
      }
      tot++;
    }
  }// 对3-6行与7-9行分别换行组合，生成其他满足条件的解。
  return result;
}
// 通过组合理论上可生成 2*6*6种数独解。

bool checkSudoku(int grid[10][10]) {
  int xx[] = { 1, 1, 1, 0, 0, -1, -1, -1 };
  int yy[] = { 1, -1, 0, 1, -1, 1, -1, 0 };
  int temp[10];
  int cnt = 0;
  bool isSudoku = true;
  for (int i = 0; i < 9; i++) {
    cnt = 0;
    for (int j = 0; j < 9; j++) {
      temp[cnt++] = grid[j][i];
    }
    if (!checkdiff(temp, 9)) return false;
  } // 判断每一列的情况
  for (int i = 0; i < 9; i++) if (!checkdiff(grid[i], 9)) return false; //判断每一行的情况
  for (int i = 1; i < 9; i += 3) {
    for (int j = 1; j < 9; j += 3) {
      cnt = 0;
      temp[cnt++] = grid[i][j];
      for (int k = 0; k < 8; k++) {
        temp[cnt++] = grid[i + xx[k]][j + yy[k]];
      }
      if (!checkdiff(temp, 9)) return false;
    }
  } // 判断每一个3 * 3方块的情况，
	return true;
}

---

测试运行

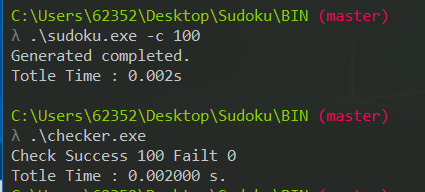
6 1 2 3 4 5 7 9 8
3 4 5 7 9 8 6 1 2
7 9 8 6 1 2 3 4 5
2 6 1 5 3 4 8 7 9
8 7 9 2 6 1 5 3 4
5 3 4 8 7 9 2 6 1
1 2 6 4 5 3 9 8 7
9 8 7 1 2 6 4 5 3
4 5 3 9 8 7 1 2 6 

6 1 2 3 4 5 7 9 8
3 4 5 7 9 8 6 1 2
7 9 8 6 1 2 3 4 5
2 6 1 5 3 4 8 7 9
8 7 9 2 6 1 5 3 4
5 3 4 8 7 9 2 6 1
4 5 3 9 8 7 1 2 6
1 2 6 4 5 3 9 8 7
9 8 7 1 2 6 4 5 3 

6 1 2 3 4 5 7 9 8
3 4 5 7 9 8 6 1 2
7 9 8 6 1 2 3 4 5
2 6 1 5 3 4 8 7 9
8 7 9 2 6 1 5 3 4
5 3 4 8 7 9 2 6 1
4 5 3 9 8 7 1 2 6
9 8 7 1 2 6 4 5 3
1 2 6 4 5 3 9 8 7
...

---

性能分析

复杂度：

预估： 假设生成全排列(next_permutation)的复杂度为O(n!), generator(n)的构造函数复杂度为O(9!), generateGrid()的复杂度为O（3！*3！*9*9） 假设需要生成的数独解个数为n 那么复杂度大约为O(9! + n / 25 * 3！*3！*9*9) ≈ 1e8 所耗 CPU 预估小于1000ms 再加上输出到文件的IO操作，大概时间约为1000ms。

性能分析图

性能优化

个人认为，优化可以从输出到文件的IO操作中入手，可以适当增加运行内存当作缓冲区，再输出到文件。

---

单元测试

单元测试结果

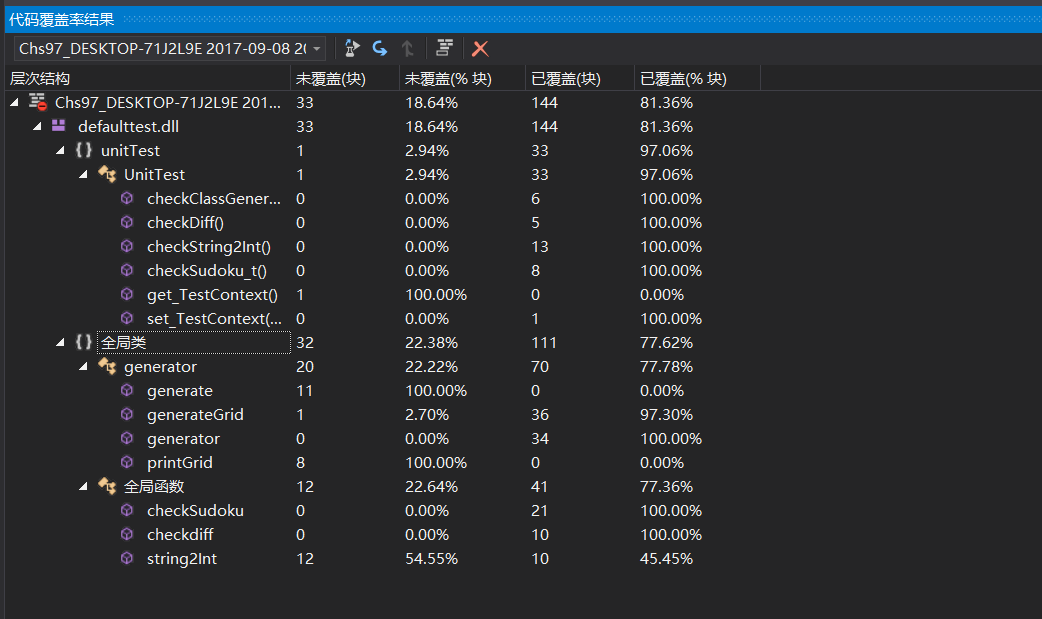
覆盖率测试

---

PSP分析

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	12	20
· Estimate	· 估计这个任务需要多少时间	12	20
Development	开发	350	515
· Analysis	· 需求分析 (包括学习新技术)	60	180
· Design Spec	· 生成设计文档	20	40
· Design Review	· 设计复审 (和同事审核设计文档)	0	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	15
· Design	· 具体设计	30	30
· Coding	· 具体编码	120	150
· Code Review	· 代码复审	30	40
· Test	· 测试（自我测试，修改代码，提交修改）	60	60
Reporting	报告	65	85
· Test Report	· 测试报告	15	15
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	40	60
合计		427	620

---

其他

结合上次作业的评分总结，在博客中谈谈你关于 执行力 、 泛泛而谈 的理解，好与不好都必须列举实际例子、数据或推理加以说明。

执行力：个人认为，执行力就是对于需要做的想要做的事情，是立马去做，还是拖了很久才做。并且做的过程应该是认真的，不是应付的。我觉得我的执行力确实不怎么样，5月份在todolist上的事情，拖到了8月份才做，甚至，8月份只做了一半，感觉周围的诱惑有点多，什么斗鱼直播，csgo，王者荣耀...，关于怎么提高执行力呢，，我也不知道。

泛泛而谈: 大概，在以后的简历上总会出现：熟悉，了解，掌握，这些词语对于计算机专业来说，是很难界定的。对于上个作业出现的：项目经验也比较丰富吧这句话,具体来说目前所写过的项目有： West2Join, 代代, **学车公众号，金**微信小程序，**平台超级管理后台, wonderland,以上项目的前端部分.还有就是一些自己练手的小东西。