Codeforces Round #277 (Div. 2) A B C 水 模拟 贪心

A. Calculating Function

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

For a positive integer n let's define a function f:

f(n) =  - 1 + 2 - 3 + .. + ( - 1)nn

Your task is to calculate f(n) for a given integer n.

Input

The single line contains the positive integer n (1 ≤ n ≤ 1015).

Output

Print f(n) in a single line.

Examples

input

4

output

2

input

5

output

-3

Note

f(4) =  - 1 + 2 - 3 + 4 = 2

f(5) =  - 1 + 2 - 3 + 4 - 5 =  - 3

题意：求f(n) =  - 1 + 2 - 3 + .. + ( - 1)nn

题解：水

 /******************************
 code by drizzle
 blog: www.cnblogs.com/hsd-/
 ^ ^    ^ ^
  O      O
 ******************************/
 #include<bits/stdc++.h>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<map>
 #include<algorithm>
 #include<queue>
 #define LL __int64
 #define pii pair<int,int>
 #define MP make_pair
 using namespace std;
 LL n;
 int main()
 {
     scanf("%I64d",&n);
     if(n%)
         cout<<(n-)/-n<<endl;
     else
         cout<<n/<<endl;;

     return ;
 }

B. OR in Matrix

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's define logical OR as an operation on two logical values (i. e. values that belong to the set {0, 1}) that is equal to 1 if either or both of the logical values is set to 1, otherwise it is 0. We can define logical OR of three or more logical values in the same manner:

 where 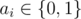 is equal to 1 if some ai = 1, otherwise it is equal to 0.

Nam has a matrix A consisting of m rows and n columns. The rows are numbered from 1 to m, columns are numbered from 1 to n. Element at row i (1 ≤ i ≤ m) and column j (1 ≤ j ≤ n) is denoted as Aij. All elements of A are either 0 or 1. From matrix A, Nam creates another matrix B of the same size using formula:

.

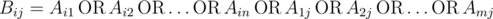(Bij is OR of all elements in row i and column j of matrix A)

Nam gives you matrix B and challenges you to guess matrix A. Although Nam is smart, he could probably make a mistake while calculating matrix B, since size of A can be large.

Input

The first line contains two integer m and n (1 ≤ m, n ≤ 100), number of rows and number of columns of matrices respectively.

The next m lines each contain n integers separated by spaces describing rows of matrix B (each element of B is either 0 or 1).

Output

In the first line, print "NO" if Nam has made a mistake when calculating B, otherwise print "YES". If the first line is "YES", then also print mrows consisting of n integers representing matrix A that can produce given matrix B. If there are several solutions print any one.

Examples

input

2 2
1 0
0 0

output

NO

input

2 3
1 1 1
1 1 1

output

YES
1 1 1
1 1 1

input

2 3
0 1 0
1 1 1

output

YES
0 0 0
0 1 0

题意：  已知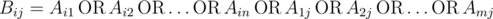. 给你 B矩阵 判断是否有对应的A矩阵

若有则输出YES 并且输出该矩阵 若没有则输出 NO

题解：  如果存在对应的A矩阵 可以很容易的发现Aij=Bi1&Bi2&....&Bin&B1j&B2j&B3j....&Bmj

如何判断是否存在满足条件的A矩阵呢？ 对于满十字(当前aij为交点的十字上都为1) c[][]标记每一个位置 与B矩阵比较

若a[i][j]&&c[i][j]==0 则不存在A矩阵 输出NO （可以举例验证） 这里的B矩阵用a[][]记录

 /******************************
 code by drizzle
 blog: www.cnblogs.com/hsd-/
 ^ ^    ^ ^
  O      O
 ******************************/
 #include<bits/stdc++.h>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<map>
 #include<algorithm>
 #include<queue>
 #define LL __int64
 #define pii pair<int,int>
 #define MP make_pair
 using namespace std;
 int m,n;
 int a[][];
 int b[][];
 int c[][];
 int main()
 {
     scanf("%d %d",&m,&n);
     memset(c,,sizeof(c));
     for(int i=;i<=m;i++)
         for(int j=;j<=n;j++)
         scanf("%d",&a[i][j]);
     for(int i=;i<=m;i++)
     {
         for(int j=;j<=n;j++)
         {
             int jishu=;
             int exm=a[][j];
             if(exm)
                 jishu++;
             for(int k=;k<=m;k++){
                 exm&=a[k][j];
                 if(a[k][j])
                     jishu++;
                 }
                 for(int k=;k<=n;k++){
                 exm&=a[i][k];
                 if(a[i][k])
                     jishu++;
                 }
             if(jishu==(n+m))
             {
                  for(int k=;k<=m;k++)
                     c[k][j]=;
                 for(int k=;k<=n;k++)
                     c[i][k]=;
             }
             b[i][j]=exm;
         }
     }
      for(int i=;i<=m;i++)
         for(int j=;j<=n;j++){
             if(a[i][j]&&c[i][j]==)
             {
                 cout<<"NO"<<endl;
                 return ;
             }
         }
     cout<<"YES"<<endl;
     for(int i=;i<=m;i++){
         for(int j=;j<=n;j++){
                 cout<<b[i][j]<<" ";
         }
         cout<<endl;
     }
     return ;
 }

C. Palindrome Transformation

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Nam is playing with a string on his computer. The string consists of n lowercase English letters. It is meaningless, so Nam decided to make the string more beautiful, that is to make it be a palindrome by using 4 arrow keys: left, right, up, down.

There is a cursor pointing at some symbol of the string. Suppose that cursor is at position i (1 ≤ i ≤ n, the string uses 1-based indexing) now. Left and right arrow keys are used to move cursor around the string. The string is cyclic, that means that when Nam presses left arrow key, the cursor will move to position i - 1 if i > 1 or to the end of the string (i. e. position n) otherwise. The same holds when he presses the right arrow key (if i = n, the cursor appears at the beginning of the string).

When Nam presses up arrow key, the letter which the text cursor is pointing to will change to the next letter in English alphabet (assuming that alphabet is also cyclic, i. e. after 'z' follows 'a'). The same holds when he presses the down arrow key.

Initially, the text cursor is at position p.

Because Nam has a lot homework to do, he wants to complete this as fast as possible. Can you help him by calculating the minimum number of arrow keys presses to make the string to be a palindrome?

Input

The first line contains two space-separated integers n (1 ≤ n ≤ 105) and p (1 ≤ p ≤ n), the length of Nam's string and the initial position of the text cursor.

The next line contains n lowercase characters of Nam's string.

Output

Print the minimum number of presses needed to change string into a palindrome.

Examples

input

8 3
aeabcaez

output

6

Note

A string is a palindrome if it reads the same forward or reversed.

In the sample test, initial Nam's string is:  (cursor position is shown bold).

In optimal solution, Nam may do 6 following steps:

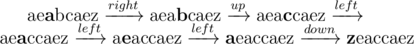
The result, 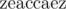, is now a palindrome.

题意：  长度与n的小写字母字符串a 起始点为第p个字母 通过4种改变方式最终使得a为回文串

问最后需要多少步？ L:左移一位 R:右移一位U:当前字符增加1 D:当前字符减少1  注意‘a’与‘z’相差1 也就是把a~z作为环状

题解：  对于需要多少步骤 首先统计一遍处于对应位置的每个字符 若不相同 则需要多少步骤才能相同

假设某个对应位置的两个字符char1<char2 需要min(char2-char1,char1+26-char2)步骤才能相同

与此同时记录左部分的l1,r1与右部分的l2,r2  代表需要变化的字符的最小位置与最大位置 之后判断p在哪一部分 与l，r的相对位置 使得移动距离最小

注意若字符串a均为同一种字符的数据

 /******************************
 code by drizzle
 blog: www.cnblogs.com/hsd-/
 ^ ^    ^ ^
  O      O
 ******************************/
 #include<bits/stdc++.h>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<map>
 #include<algorithm>
 #include<queue>
 #define LL __int64
 #define pii pair<int,int>
 #define MP make_pair
 using namespace std;
 int n,p;
 char a[];
 int main()
 {
     scanf("%d %d",&n,&p);
     p--;
     getchar();
     scanf("%s",a);
     int ans=;
     int l1=-,r1=-,l2=-,r2=-;
     int flag=;
     for(int i=;i<n/;i++)
     {
         if(a[i]!=a[n-i-])
         {
             if(flag==)
             {
                 l1=r1=i;
                 l2=r2=n-i-;
                 flag=;
             }
             else
             {
                 r1=i;
                 l2=n-i-;
             }
         char exm1=a[i],exm2=a[n-i-],zhong;
         if(exm1>exm2)
         {
             zhong=exm1;
             exm1=exm2;
             exm2=zhong;
         }
         ans=ans+min(exm2-exm1,exm1+-exm2);
         }
     }
     if(p<=(n-)/)
     {
        if(flag)
        {
        if(p<=l1)
        ans=ans+(l1-p)+r1-l1;
        else
        if(p>=r1)
        ans=ans+(p-r1)+r1-l1;
        else
        ans=ans+r1-l1+min(p-l1,r1-p);
        }
     }
     else
     {
         if(flag){
        if(p<=l2)
        ans=ans+(l2-p)+r2-l2;
        else
        if(p>=r2)
        ans=ans+(p-r2)+r2-l2;
        else
        ans=ans+r2-l2+min(p-l2,r2-p);
        }
     }
     cout<<ans<<endl;
     return ;
 }