<<薪资至少10K的一道题，你能拿下吗>>练习

　　偶尔要写写算法,是我平时用来保持感觉的常用的方法.今天看到园子里一面试题,看了一下感觉也能实现,不过过程确实艰的,自认为自己对算法的感觉还不错.不过这题确实我也用了差不多一下午的时间,基本上把工作时间都耗掉了.主要的两个方法已经搞定,下面先说一下思想,代码确实不太重要,因为过一周我自己就会看不懂了,就像我今天也去看以前的代码.因为这里用到一部分深度优先遍历,所以去找以前代码,但是完全没有作用,还是纯写.

　　

    interface IPath
    {
        /// <summary>
        /// 增加某条地铁线路
        /// </summary>
        /// <param name="lineNo">地铁线号</param>
        /// <param name="stationNum">站点数目</param>
        /// <param name="stationArray">地铁线站台号数组</param>
        void AddLine(int lineNo, int stationNum, int[] stationArray);
 
        /// <summary>
        /// 计算从超点到终点的最短路线长度
        /// </summary>
        /// <param name="srcStation">起点站</param>
        /// <param name="desStation">终点站</param>
        /// <returns>起点站到终点站最短线长度</returns>
        int CalcMinPathLen(int srcStation, int desStation);
 
        /// <summary>
        /// 输出从起点到终点的最短路线
        /// </summary>
        /// <param name="srcStation">起点</param>
        /// <param name="desStation">终点</param>
        /// <param name="pathNum">条数</param>
        /// <param name="pathLen">长度</param>
        /// <param name="pathes">结果路线集合</param>
        /// <returns>0成功 -1出错</returns>
        int SearchMinPaths(int srcStation, int desStation, out int pathNum, out int pathLen, out int[][] pathes);
 
        /// <summary>
        /// 最优路线
        /// </summary>
        /// <param name="srcStation">起点</param>
        /// <param name="desStation">终点</param>
        /// <param name="pathNum">条数</param>
        /// <param name="pathLen">长度</param>
        /// <param name="pathes">结果路线集合</param>
        /// <returns>0成功 -1出错</returns>
        int SearchBestPathes(int srcStation, int desStation, out int pathNum, out int pathLen, out int[][] pathes);
 
    }

其实这个从题目中命名等看出来主要是C++题,本人用C#实现,其实可以改一些参数名称更为方便,但是这里就按题目中接口来吧.AddLine方法就不说了.

int CalcMinPathLen(int srcStation, int desStation);

计算最短路径,这里用的是迪杰斯特拉算法,就是从起点按起点到各各点最短距离来一个一个往集合里面添加,当然这里的距离就是1,如果是其它数字也是可以的.

int SearchMinPaths(int srcStation, int desStation, out int pathNum, out int pathLen, out int[][] pathes);

这个方法其实略坑了,我基本上是重新想的解决办法,同第一个方法没有很大的联系,不知道我这种思考是否是最优的,不过是可以解决的.重点地方就是用到一个变异的深度优先遍历,这个是有环路存在的,所以比树的深度优先遍历要复杂一些,注意一下深度就可以了,用到一个深度变量去控制是不是保留在遍历排除集合中,就是方法中的list.

两个方法代码如下

    public class MetroPath : IPath
    {
        private readonly List<Tuple<int, int, int[]>> pathes;
        private int stationCount = ;
 
        private List<int> minStations;
 
        public MetroPath()
        {
            pathes = new List<Tuple<int, int, int[]>>();
            minStations = new List<int>();
        }
 
        public void AddLine(int lineNo, int stationNum, int[] stationArray)
        {
            if (stationNum <  || stationArray == null || stationArray.Length != stationNum)
                Console.WriteLine("站点数目不对");
            else
                pathes.Add(new Tuple<int, int, int[]>(lineNo, stationNum, stationArray));
        }
 
        public int CalcMinPathLen(int srcStation, int desStation)
        {
            //用迪杰斯特拉算法计算
            Dictionary<int, int> stationLens = new Dictionary<int, int>();
 
            IEnumerable<int> ct = pathes[].Item3;
            //得到所有站数
            foreach (var a in pathes)
            {
                ct = ct.Union(a.Item3);
            }
            stationCount = ct.Distinct().Count();
 
            try
            {
                stationLens.Add(srcStation, );//初始
 
                while (stationLens.Count < stationCount)
                {
                    stationLens = FindMinStation(stationLens, srcStation);
                }
 
                //下一题用
                minStations = stationLens.Select(x => x.Key).ToList();
 
                //找出起点到终点最短长度
                return stationLens[desStation];
            }
            catch
            {
                return -; //出错
            }
        }
 
        //找出余下站点中最短的站点及起点到它的长度
        private Dictionary<int, int> FindMinStation(Dictionary<int, int> stations, int srcStation)
        {
            Dictionary<int, int> lens = new Dictionary<int, int>();
 
            foreach (var p in pathes)
            {
                foreach (var station in p.Item3)
                {
                    if (!stations.ContainsKey(station))
                    {
                        //计算最小值
                        var minlen = ReachLen(stations, srcStation, station);
                        if (minlen >  && !lens.ContainsKey(station))
                            lens.Add(station, minlen);
                    }
                }
            }
 
            //找出lens中最小的(可以多个)加入集合
            int min = lens.Min(v => v.Value);
 
            return stations.Union(lens.Where(x => x.Value == min)).ToDictionary(k => k.Key, v => v.Value);
        }
 
        //是否是可达的 -1为不可达
        private int ReachLen(Dictionary<int, int> stations, int srcStatoin, int station)
        {
            List<int> reachStations = new List<int>();
            foreach (var p in pathes)
            {
                for (int i = ; i < p.Item3.Length; i++)
                {
                    if (p.Item3[i] == station)
                    {
                        if (i -  >=  && !reachStations.Contains(p.Item3[i - ]))
                            reachStations.Add(p.Item3[i - ]);
                        if (i +  < p.Item3.Length && !reachStations.Contains(p.Item3[i + ]))
                            reachStations.Add(p.Item3[i + ]);
                    }
                }
            }
 
            var q = stations.Where(v => reachStations.Contains(v.Key));
            //相邻点不在集合里面
            if (q == null || q.Count() <= )
                return -;
            else
            {
                //找出q中最小的值
                return q.OrderByDescending(v => v.Value).First().Value + ;
            }
 
        }
 
        public int SearchMinPaths(int srcStation, int desStation, out int pathNum, out int pathLen, out int[][] pathes)
        {
            pathNum = ;
            pathLen = ;
            pathes = null;
 
            try
            {
                pathLen = CalcMinPathLen(srcStation, desStation);
 
                List<int[]> result = new List<int[]>();
 
                Stack<int> sk1 = new Stack<int>();
                List<Tuple<int, int>> list = new List<Tuple<int, int>>();
 
                sk1.Push(srcStation);
                minStations.Remove(srcStation);
 
                int ct = ;
                int deepth = ;
                while (deepth > )
                {
                    bool flag = false;
                    foreach (var x in minStations)
                    {
                        list.RemoveAll(v => v.Item1 > deepth);
 
                        if (ExistsRalation(sk1.Peek(), x) && !sk1.Contains(x) && list.Where(v => v.Item2 == x).Count() <= )
                        {
                            sk1.Push(x);
                            deepth++;
                            flag = true;
                            break;
                        }
                    }
 
                    //
                    if (sk1.Peek() == desStation)
                    {
                        //一条完整的路线
                        result.Add(sk1.Reverse().ToArray());
                        deepth--;
                        list.Add(new Tuple<int, int>(deepth, sk1.Pop()));
                        ct++;
                    }
                    //没有找到
                    if (!flag)
                    {
                        deepth--;
                        list.Add(new Tuple<int, int>(deepth, sk1.Pop()));
                    }
                }
 
                pathNum = ct;
                pathes = result.ToArray();
                return ;
            }
            catch
            {
                return -;
            }
 
        }
 
        private bool ExistsRalation(int a, int b)
        {
            if (a == b)
                return false;
 
            foreach (var p in pathes.Where(x => x.Item3.Contains(a) && x.Item3.Contains(b)))
            {
                for (int i = ; i < p.Item3.Length; i++)
                {
                    if (p.Item3[i] == a)
                    {
                        if (i -  >=  && p.Item3[i - ] == b)
                            return true;
                        if (i +  < p.Item3.Length && p.Item3[i + ] == b)
                            return true;
                    }
                }
            }
            return false;
 
        }
 
        public int SearchBestPathes(int srcStation, int desStation, out int pathNum, out int pathLen, out int[][] pathes)
        {
            throw new NotImplementedException();
        }
    }

最后一个方法还没有实现,不过大思路也还是可以有的,路径找出来了,只要看路径上交乘点多少就可以了,越少越优,这个算简单.没有时间写了.

最后是调用代码和结果

            //测试
            IPath mp = new MetroPath();
            mp.AddLine(, , new int[] { , , , ,  });
            mp.AddLine(, , new int[] { , , , ,  });
            mp.AddLine(, , new int[] { , ,  });
            mp.AddLine(, , new int[] { ,  });
 
            var min = mp.CalcMinPathLen(, );
            Console.WriteLine("从1到11最短路径长度为:{0}", min);
 
            int pathNum = ;
            int pathLen = ;
            int[][] pathes = null;
            var re = mp.SearchMinPaths(, , out pathNum, out pathLen, out pathes);
 
            Console.WriteLine("从1到11最短路径条数为{0},分别是", pathNum);
            foreach (var x in pathes)
            {
                Console.Write("\n{");
                foreach (var i in x)
                {
                    Console.Write("{0},", i);
                }
                Console.Write("}\n");
            }
 
            Console.ReadLine();

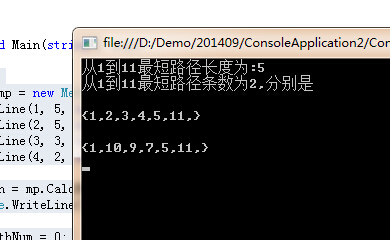
对题中的数据来看是正常的.个人觉得本题还是有难度的,特别是要实实在在写出来,并且调通,我看文中评论有些说简单的人请去实践一下再说吧.

插个小插曲,就是代码一写过基本上就看不懂了.刚才我说到我查阅深度优先算法,我自己的代码完全看不懂,不过看起来以前写的还是很简练,不过是对简单图的遍历.

        /// <summary>
        /// 深度优先
        /// </summary>
        static void DFS(int[,] a, int n)
        {
            Stack<int> sk1 = new Stack<int>();
            Stack<int> sk2 = new Stack<int>();
            sk1.Push();
            Console.WriteLine();
            int x = ;//访问点标记
 
            int ct = ;//访问节点数
            while (ct < n)
            {
                int i = ;
                bool f = false;
                for (i = ; i < n; i++)
                {
                    if (a[x, i] !=  && !sk2.Contains(i))
                    {
                        sk1.Push(i);
                        Console.WriteLine(i); ct++;
                        x = i;
 
                        f = true;
                        break;
                    }
                }
                if (!f)
                {
                    //没有找到返回
                    sk2.Push(sk1.Pop());
                    x = sk1.Peek();
                }
 
            }
        }

确实比较短的,不过看不懂.所以主要还是在于思想吧.数据测试

            int[,] a = {
                       {,,,,}
                       ,{,,,,}
                       ,{,,,,}
                       ,{,,,,}
                       ,{,,,,}
                   };
 
            Console.WriteLine("DFS:");
            DFS(a, );
            Console.Read();

　　最后总结:　　

　　　　1.理解迪杰斯特拉算法

　　　　2.深度优先遍历,主要用栈,广度优先主要考虑队列.

　　　　3.深度优先的冲突处理,考虑用深度变量.