OJ最大值最小化问题（分发书本）

该类问题通用描述：

　　有n个物体，每个物体都有一个权值V[i],现在将n个物体连续分成m个部分，m个部分有一个部分会拿到最多的权值v。求所有分配方式中最小的v。

典型题目：

　　分发书本，宠物屋涂色等。

问题分析：

 　   为便于问题理解，将n个物品权值当成物体体积V，每个物体体积V[i]。分成m个部分表示用m个桶去顺序装这些物品，那么问题就变成了用m个容量相同的桶子去装这些物品，桶子的容量最小可以为多少。如下图所示：

　　

　　我们设定满足条件的最小桶子容量为target，那么怎么确定target值呢？我们可以先假设桶子容量都为x，然后按顺序将物品放入到桶子中，如果放不下了就放入下一个。如果放满最后一个桶，物品还没放完，那么桶子容量肯定小了，即x < target;如果在放满最后一个桶前，物品放完了，那么桶子容量大了或刚好适合，即x >= target。

　　我们接着来确定桶子容量target的范围，target首先要能装任何一个物品，所以target >= max(max指体积最大的物品的体积），同时target <= sum(sum指所有物品的体积和)。

　　到了现在我们知道target的范围，也知道如何判断一个数x与target的大小关系。为了减少比较次数，可以使用二分法来找到具体的值。和普通的二分查找不同的是需要通过更多计算（判断容量为x时能否放完全部物品）得到中值与target的大小关系，进而进一步确定范围。

　　java版本的实现代码（含注释）如下：

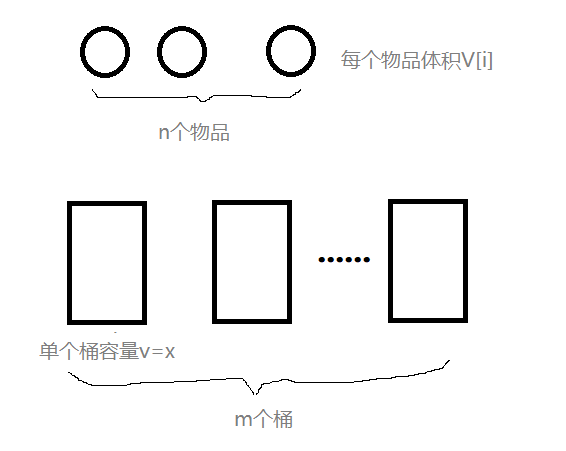
 1 // 相当于有n个物品，每个物品的体积V[i],要使得m个容量相同的桶能按顺序装下所有物品，求出桶的最小容量target
 2 public int splitArray(int[] V, int m){
 3     // 待求解值target的范围为[max,sum]
 4     int max =  V[0];
 5     int sum = V[0];
 6     for (int i = 1; i < V.length; i++) {
 7         max = Math.max(max,V[i]);
 8         sum += V[i];
 9     }
10     // 二分法找到target值
11     int left = max;
12     int right = sum;
13     while (left < right) {
14         int mid = (left+right)/2;
15         // 判断当桶子容量为mid时能否装完所有物品,能装完则target <= mid, 不能装完则target > mid
16         if (isFit(V,mid,m)) {
17             right = mid;
18         } else {
19             left = mid+1;
20         }
21     }
22     return left;
23 }
24 // 判断当桶子容量为x时m个桶子能否装完所有物品,true表示可以装完物品，false表示还没装完
25 public boolean isFit(int[] V, int x, int m) {
26     // 当前桶数
27     int count = 1;
28     // 当前桶被填容量
29     int s = 0;
30     for (int i = 0; i < V.length; i++) {
31         // 没超过一个桶容量就放到该桶
32         if (s + V[i] <= x) {
33             s += V[i];
34         } else {
35             // 超过一个桶容量就把该物品放到下一个桶，并把桶数+1
36             s = V[i];
37             count++;
38         }
39     }
40     // 判断桶数是否超过x，count<=x表示没装完桶子，返回true，count>x表示桶子数不够没装完，返回false
41     if (count <= m)
42         return true;
43     else
44         return false;
45 }