JQuery 选择器：

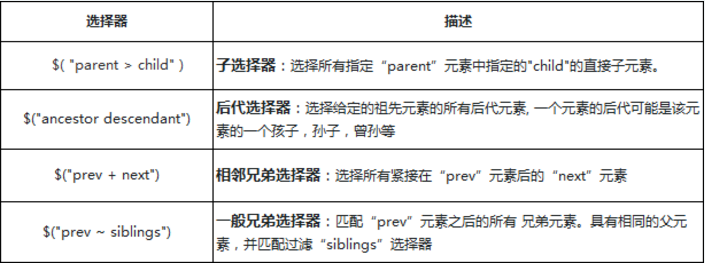
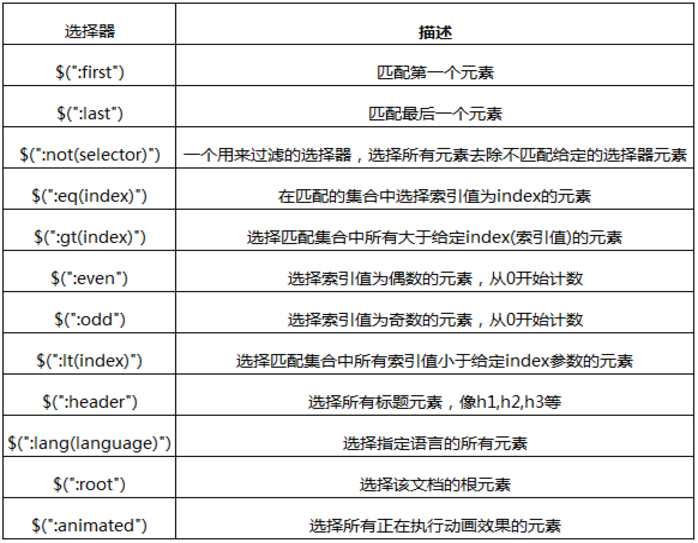
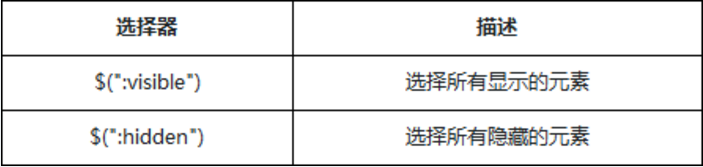
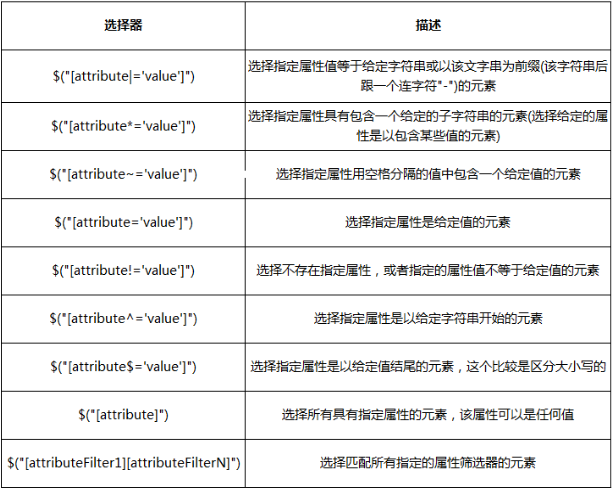
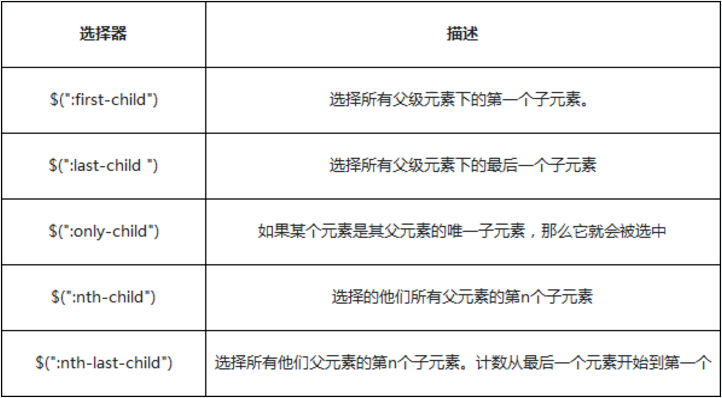
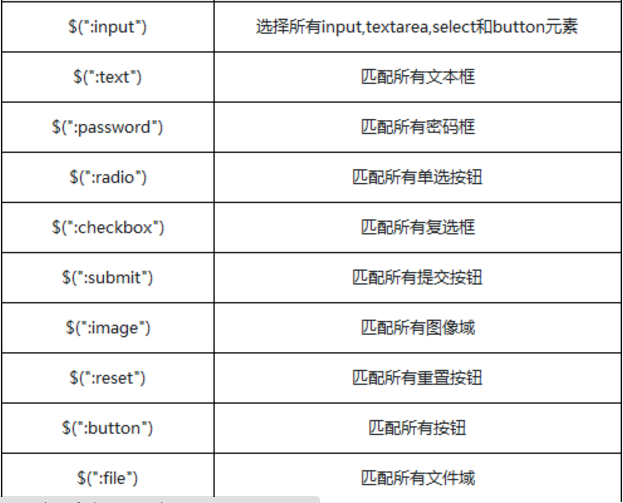
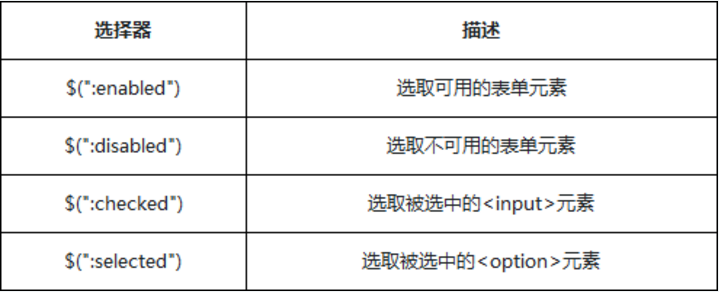
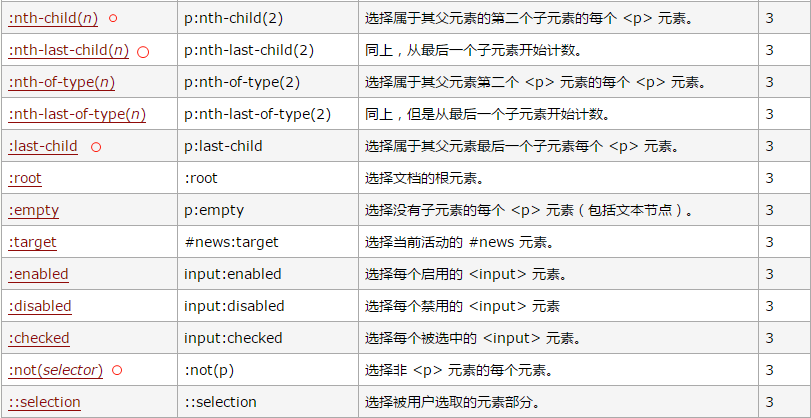
CSS 选择器：

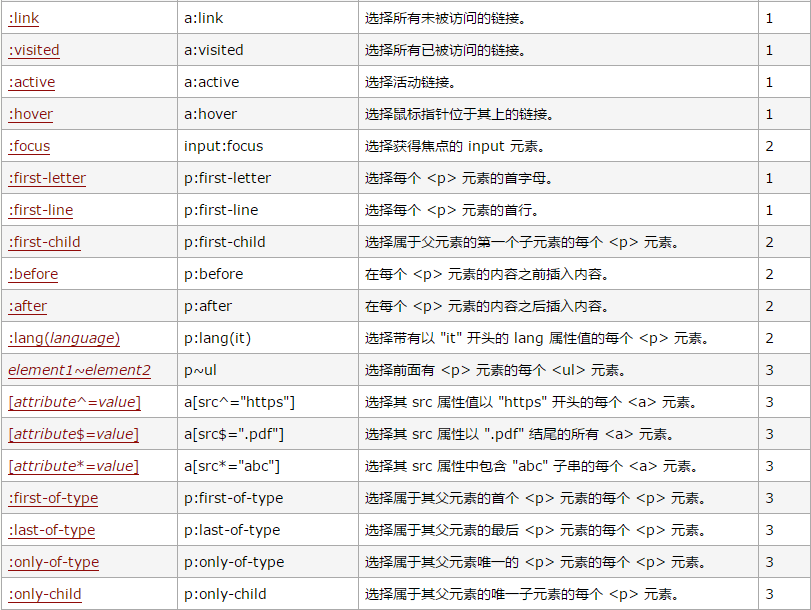
JQuery 和 CSS 等选择器：的更多相关文章

  1. 前端笔记之jQuery（上）加载函数的区别&对象&操作HTML/CSS&动画&选择器

    一.jQuery简介 1.0 JavaScript编程比较恶心的地方 恶心1:选择元素麻烦,全线兼容的方法只有getElementById()和getElementsByTagName()两个.其他的 ...

  2. CSS的选择器

    <div id="demo"> <div class="inner"> <p><a href="#" ...

  3. jQuery入门（1）jQuery中万能的选择器

    jQuery入门(1)jQuery中万能的选择器 jQuery入门(2)使用jQuery操作元素的属性与样式 jQuery入门(3)事件与事件对象 jQuery入门(4)jQuery中的Ajax()应 ...

  4. jquery笔记之属性选择器 查找以某种条件开头的页面元素

    jquery笔记之属性选择器 查找以某种条件开头的页面元素 转载:http://www.blogbus.com/amyqiong-logs/78340326.html $("div[id]& ...

  5. 从零开始学习jQuery (二) 万能的选择器

    本系列文章导航 从零开始学习jQuery (二) 万能的选择器 一.摘要 本章讲解jQuery最重要的选择器部分的知识. 有了jQuery的选择器我们几乎可以获取页面上任意的一个或一组对象, 可以明显 ...

  6. jquery和css自定义video播放控件

    下面介绍一下通过jquery和css自定义video播放控件. Html5 Video是现在html5最流行的功能之一,得到了大多数最新版本的浏览器支持.包括IE9,也是如此.不同的浏览器提供了不同的 ...

  7. IE7浏览器下CSS属性选择器二三事

    一.为何专门说起IE7 以前,或者说数年前,我们从事桌面端网页开发的时候,基本上都还要兼顾IE6浏览器, 即使有些特性,IE7支持,我们也会忽略之.于是,我们会不自然地把IE6和IE7浏览器归为一路货 ...

  8. JQuery - 改变css样式

    jQuery提供css()的方法来实现嵌入式改变元素样式,css()方法在使用上具有多样性.其中一种接受两个输入参数:样式属性和样式值,它们之间用逗号分开.比如我们要改变链接颜色,我们可以使用下面的代 ...

  9. jQuery（2）——选择器

    选择器 利用jQuery选择器,可以非常便捷和快速地找出特定的DOM元素,然后为它们添加相应的行为.jQuery的行为规则都必须在获取到元素后才能生效. [jQuery选择器的优势] (1)简洁的写法 ...

随机推荐

  1. Spring Boot 面试总结

    1.使用 Spring Boot 前景? 多年来,随着新功能的增加,spring变得越来越复杂.只需访问https://spring.io/projects页面,我们就会看到可以在我们的应用程序中使用 ...

  2. Python知识整理（一）

    一.Python交互模式(终端上进行) python # 进入到Python交互模式,提示符是 >>> exit() # 退出Python交互模式 python xxx.py # 执 ...

  3. idea创建maven项目时一直在 Process Running

    解决方案: 1.设置maven的配置 File--->Settings(Ctrl+Alt+S)--->Build--->Build Tools--->Maven--->R ...

  4. 使用bs4中的方法爬取星巴克数据

    import urllib.request # 请求url url = 'https://www.starbucks.com.cn/menu/' # 模拟浏览器发出请求 response = urll ...

  5. 菜鸡的Java笔记 第二十六 - java 内部类

    /*    innerClass        从实际的开发来看,真正写到内部类的时候是在很久以后了,短期内如果是自己编写代码,几乎是见不到内部类出现的        讲解它的目的第一个是为了解释概念 ...

  6. File与IO基础

    IO流的作用:持久化到磁盘 File类的使用 File类基本概念 文件和文件夹都是用File类来表示. File类是内存层面的对象,内存中创建出来的File对象不一定有一个真实存在的文件或文件夹,但是 ...

  7. LG 11 月 月赛 II T4

    LG 11 月 月赛 II T4 看到膜数和 $ 10^5 $ 以及 $ n^2 $ 的部分分想到很可能是 NTT 于是开始推式子 首先看到式子可以化作, 如果 \(k = 0\) , $ f(l , ...

  8. SUNTANS 及 FVCOM 对流扩散方程求解简介［TBC］

    最近接到一个任务,就是解决FVCOM中对流扩散计算不守衡问题.导师认为是其求解时候水平和垂向计算分开求解所导致的,目前我也没搞清到底有什么问题,反正就是让把SUNTANS的对流扩散计算挪到FVCOM中 ...

  9. R数据科学-3

    R数据科学(R for Data Science) Part 3:编程 转换--可视化--模型 --------------第13章 使用magrittr进行管道操作----------------- ...

  10. 40-3Sum Closest

    3Sum Closest My Submissions QuestionEditorial Solution Total Accepted: 76185 Total Submissions: 2621 ...