单源最短路径算法：迪杰斯特拉 (Dijkstra) 算法（二）

一、基于邻接表的Dijkstra算法

　　如前一篇文章所述，在 Dijkstra 的算法中，维护了两组，一组包含已经包含在最短路径树中的顶点列表，另一组包含尚未包含的顶点。使用邻接表表示，可以使用 BFS 在O（V + E）时间中遍历图的所有顶点  。这个想法是使用 BFS 遍历图的所有顶点，并使用最小堆存储尚未包括在最短路径树中的顶点（或尚未确定最短距离的顶点）。最小堆用作优先级队列，以从尚未包括的顶点集中获取最小距离顶点。对于Min Heap，诸如 extract-min 和 reduce-key 值之类的操作的时间复杂度为 O（logV）。使用邻接表表示的 Dijkstra算法时间复杂度为 O（ELogV）。

二、详细步骤

　　1） 创建大小为 V 的最小堆，其中 V 是给定图中的顶点数。最小堆的每个节点都包含顶点数和顶点的距离值。
　　2） 以源顶点为根初始化 Min Heap（分配给源顶点的距离值为 0）。分配给所有其他顶点的距离值为 INF（无穷大）。
　　3） 当“最小堆”不为空时，执行以下操作：

• • 从“最小堆”中提取具有最小距离值节点的顶点。让提取的顶点为u。

• • 对于u的每个相邻顶点v，检查v是否在Min Heap中。如果 v 在“最小堆”中，并且距离值大于uv 的权重加上 u 的距离值，则更新 v 的距离值。

　　用下面的例子来理解。让给定的源顶点为 0：

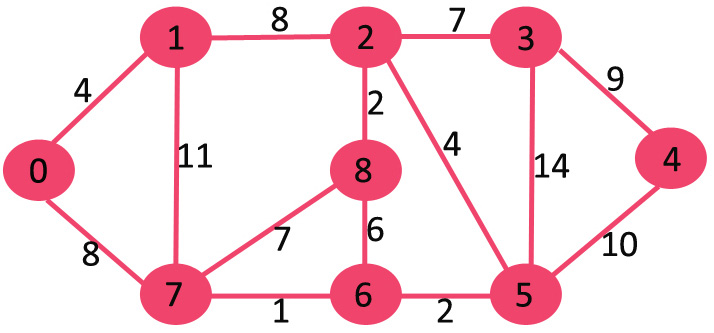
　　最初，源顶点到达自身的距离值为 0，对于所有其他顶点，INF 为无穷大。因此，从“最小堆”中提取源顶点，并更新与 0（1和7）相邻的顶点的距离值。“最小堆”包含除顶点 0 以外的所有顶点。绿色的顶点是确定了最小距离的顶点，并且不在“最小堆”中。

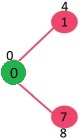
　　由于顶点1 的距离值在最小堆中的所有节点中最小，因此从最小堆中提取顶点，并更新与 1 相邻的顶点的距离值（如果顶点不在最小堆中且距离 1 的距离较短，则更新距离比之前的距离）。最小堆包含除顶点0 和 1 以外的所有顶点。

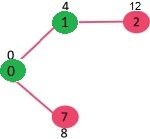
　　从最小堆中选取最小距离值的顶点。选择了顶点7。因此，最小堆现在包含除 0、1 和 7 以外的所有顶点。更新相邻 顶点7 的距离值。顶点6 和 8 的距离值变得有限（分别为15和9）。

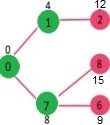
　　选择与最小堆的距离最小的顶点。选择了顶点6。因此，最小堆现在包含除 0、1、7 和 6 以外的所有顶点。更新相邻顶点6的距离值。更新顶点5 和 8 的距离值。

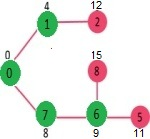
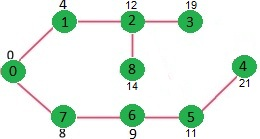
　　重复上述步骤，直到最小堆为空为止。最后，我们得到以下最短路径树。

三、代码

　　下面是使用了邻接矩阵的迪杰斯特拉算法实现。

 1     /**
 2      * 使用邻接表来实现Dijkstra的单源最短路径算法的函数
 3      *
 4      * @param adj 邻接表
 5      * @param src 源顶点
 6      */
 7     public void dijkstra(List<List<Node>> adj, int src) {
 8         this.adj = adj;
 9         for (int i = 0; i < V; i++) {
10             dist[i] = Integer.MAX_VALUE;
11         }
12
13         /* 将源节点添加到优先级队列 */
14         pq.add(new Node(src, 0));
15
16         /* 源顶点与其自身的距离始终为0 */
17         dist[src] = 0;
18
19         while (settled.size() != V) {
20             int u = pq.remove().node;
21             settled.add(u);
22             e_Neighbours(u);
23         }
24     }

　　处理传递的节点的所有邻居。

 1     /**
 2      * 处理传递过来的节点的所有邻居
 3      *
 4      * @param u
 5      */
 6     private void e_Neighbours(int u) {
 7         int edgeDistance = -1;
 8         int newDistance = -1;
 9
10         /* v的所有邻居 */
11         for (int i = 0; i < adj.get(u).size(); i++) {
12             Node v = adj.get(u).get(i);
13
14             /* 如果当前节点尚未处理 */
15             if (!settled.contains(v.node)) {
16                 edgeDistance = v.cost;
17                 newDistance = dist[u] + edgeDistance;
18
19                 /* 如果新距离的成本更低 */
20                 if (newDistance < dist[v.node])
21                     dist[v.node] = newDistance;
22
23                 /* 将当前节点添加到队列 */
24                 pq.add(new Node(v.node, dist[v.node]));
25             }
26         }
27     }

 源代码：

  1 package algorithm.shortestpath;
  2
  3 import java.util.*;
  4
  5 public class DijkstraPQ {
  6     private int[] dist;             // 当前的距离数组
  7     private Set<Integer> settled;   // 存储最短路径处理完的顶点Set集合
  8     private PriorityQueue<Node> pq; // 优先级队列(min-heap)
  9     private int V;                  // 顶点数量
 10     List<List<Node>> adj;           // 邻接表
 11
 12     public DijkstraPQ(int v) {
 13         this.V = v;
 14         dist = new int[V];
 15         settled = new HashSet<>();
 16         pq = new PriorityQueue<>(V, new Node());
 17     }
 18
 19     /**
 20      * 使用邻接表来实现Dijkstra的单源最短路径算法的函数
 21      *
 22      * @param adj 邻接表
 23      * @param src 源顶点
 24      */
 25     public void dijkstra(List<List<Node>> adj, int src) {
 26         this.adj = adj;
 27         for (int i = 0; i < V; i++) {
 28             dist[i] = Integer.MAX_VALUE;
 29         }
 30
 31         /* 将源节点添加到优先级队列 */
 32         pq.add(new Node(src, 0));
 33
 34         /* 源顶点与其自身的距离始终为0 */
 35         dist[src] = 0;
 36
 37         while (settled.size() != V) {
 38             int u = pq.remove().node;
 39             settled.add(u);
 40             e_Neighbours(u);
 41         }
 42     }
 43
 44     /**
 45      * 处理传递的节点的所有邻居的函数
 46      *
 47      * @param u
 48      */
 49     private void e_Neighbours(int u) {
 50         int edgeDistance = -1;
 51         int newDistance = -1;
 52
 53         /* v的所有邻居 */
 54         for (int i = 0; i < adj.get(u).size(); i++) {
 55             Node v = adj.get(u).get(i);
 56
 57             /* 如果当前节点尚未处理 */
 58             if (!settled.contains(v.node)) {
 59                 edgeDistance = v.cost;
 60                 newDistance = dist[u] + edgeDistance;
 61
 62                 /* 如果新距离的成本更低 */
 63                 if (newDistance < dist[v.node])
 64                     dist[v.node] = newDistance;
 65
 66                 /* 更新后将当前节点添加到最小堆中 */
 67                 pq.add(new Node(v.node, dist[v.node]));
 68             }
 69         }
 70     }
 71
 72     /**
 73      * 测试主函数
 74      *
 75      * @param args
 76      */
 77     public static void main(String[] args) {
 78         int V = 5;
 79         int source = 0;
 80         List<List<Node>> adj = new ArrayList<>();
 81
 82         for (int i = 0;i < V; i++) {
 83             List<Node> item = new ArrayList<>();
 84             adj.add(item);
 85         }
 86
 87         // 邻接表的输入
 88         adj.get(0).add(new Node(1, 9));
 89         adj.get(0).add(new Node(2, 6));
 90         adj.get(0).add(new Node(3, 5));
 91         adj.get(0).add(new Node(4, 3));
 92
 93         adj.get(2).add(new Node(1, 2));
 94         adj.get(2).add(new Node(3, 4));
 95
 96         DijkstraPQ dijkstraPQ = new DijkstraPQ(V);
 97         dijkstraPQ.dijkstra(adj, source);
 98
 99         System.out.println("The shortest path form node: ");
100         for (int i = 0; i < dijkstraPQ.dist.length; i++) {
101             System.out.println(source + " to " + i + " is " + dijkstraPQ.dist[i]);
102         }
103     }
104 }
105
106 class Node implements Comparator<Node> {
107
108     public int node;    // 顶点数
109     public int cost;    // 顶点的距离值
110
111     public Node() {
112     }
113
114     public Node(int node, int cost) {
115         this.node = node;
116         this.cost = cost;
117     }
118
119     @Override
120     public int compare(Node o1, Node o2) {
121         if (o1.cost < o2.cost)
122             return -1;
123         if (o1.cost > o2.cost)
124             return 1;
125         return 0;
126     }
127 }