题解 poj3585 Accumulation Degree （树形dp）（二次扫描和换根法）

写一篇题解，以纪念调了一个小时的经历（就是因为边的数组没有乘2 phhhh QAQ）

---

题目

题目大意：找一个点使得从这个点出发作为源点，流出的流量最大，输出这个最大的流量。

以这道题来介绍二次扫描和换根法

作为一道不定根的树形DP，如果直接对每个点进行DP，可能时间会炸掉

但是，优秀的二次换根和扫描法可以再O(n^2)内解决问题。

二次扫描的含义：（来自lyd 算法竞赛进阶指南）

第一次扫描：任选一个节点为根节点（我会选1）在树上进行树形DP，在回溯时，从儿子节点向父节点（从底向上）进行状态转移

第二次扫描：从刚才选的根出发，对树进行dfs，在每次递归前进行自顶向下的推导,计算"换根"后的解

在第一次扫描时，我们可以算出以节点u为根的子树中，从u流向其子树的最大流量

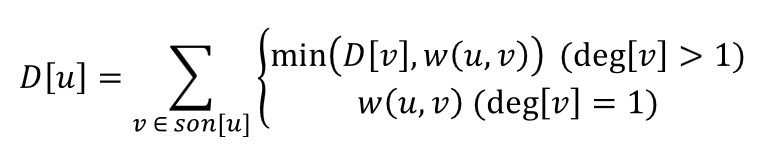
在第二次扫描时，我们通过dfs，可以自上而下的求出以节点u为根，从u流向整个流域（其子树）的最大流量

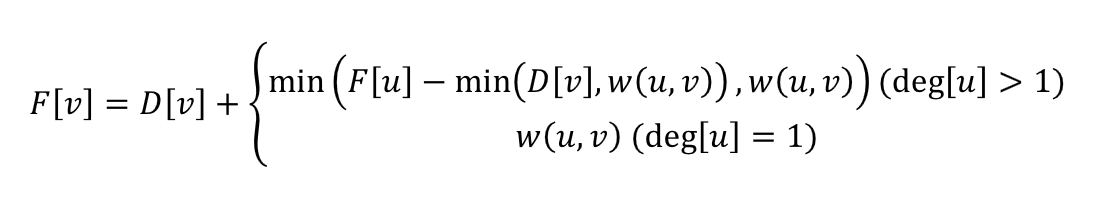
当我们从节点u到节点v时，已经求出F[u]，而从u到v的流量为min(D[v],w(u,v))，所以从u流向v的其他部分的流量就是F[u]-min(D[v],w(u,v))，所以拿它再跟w(u,v)取min

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define R register int
using namespace std;
const int N=;
struct edge{
    int v,nxt,w;
}e[N<<];
int t,n,ans,cnt;
int d[N],f[N],fir[N],deg[N];
bool vis[N];

inline void add(int u,int v,int w) {e[++cnt].v=v,e[cnt].w=w,e[cnt].nxt=fir[u],fir[u]=cnt;}

inline int g()
{
    R ret=,fix=; register char ch;
    while(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
    do ret=(ret<<)+(ret<<)+(ch^); while(isdigit(ch=getchar()));
    return ret*fix;
}

void dp(int u)
{
    vis[u]=true,d[u]=;
    for(R i=fir[u];i;i=e[i].nxt)
    {
        R v=e[i].v; if(vis[v]) continue;
        dp(v);
        if(deg[v]==) d[u]+=e[i].w;
        else d[u]+=min(d[v],e[i].w);
    }
}

void dfs(int u)
{
    vis[u]=true;
    for(R i=fir[u];i;i=e[i].nxt)
    {
        R v=e[i].v; if(vis[v]) continue;
        if(deg[u]==) f[v]=d[v]+e[i].w;
        else f[v]=d[v]+min(f[u]-min(d[v],e[i].w),e[i].w);
        dfs(v);
    }
}

int main()
{
    t=g();
    while(t--)
    {
        memset(vis,false,sizeof(vis));
        memset(fir,,sizeof(fir));
        memset(deg,,sizeof(deg)); ans=,cnt=;
        n=g();
        if(n==||n==) {putchar(''),putchar('\n');continue;}
        for(R i=;i<n;i++) {R u=g(),v=g(),w=g(); add(u,v,w),add(v,u,w); deg[u]++,deg[v]++;}
        R rt=;
        dp(rt); f[rt]=d[rt];
        memset(vis,false,sizeof(vis));
        dfs(rt);
        for(R i=;i<=n;i++) ans=max(ans,f[i]);
        printf("%d\n",ans);
    }
    return ;
}

（我太菜了。。。。QAQ）

如有错误，恳请您指正（我太菜了）；如有不理解，可留言，我会尽量回复。。。（高中生(逃)。。）

by Jackpei 2019.2.22