CS231n 2016 通关 第四章-NN 作业

cell 1 显示设置初始化

 # A bit of setup

 import numpy as np
 import matplotlib.pyplot as plt

 from cs231n.classifiers.neural_net import TwoLayerNet

 %matplotlib inline
 plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
 plt.rcParams['image.interpolation'] = 'nearest'
 plt.rcParams['image.cmap'] = 'gray'

 # for auto-reloading external modules
 # see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
 %load_ext autoreload
 %autoreload 2

 def rel_error(x, y):
   """ returns relative error """
   return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))

cell 2 网络模型与数据初始化函数

 # Create a small net and some toy data to check your implementations.
 # Note that we set the random seed for repeatable experiments.

 input_size = 4
 hidden_size = 10
 num_classes = 3
 num_inputs = 5

 def init_toy_model():
   np.random.seed(0)
   return TwoLayerNet(input_size, hidden_size, num_classes, std=1e-1)

 def init_toy_data():
   np.random.seed(1)
   X = 10 * np.random.randn(num_inputs, input_size)
   y = np.array([0, 1, 2, 2, 1])
   return X, y

 net = init_toy_model()
 X, y = init_toy_data()

　　通过末尾的调用，生成了NN类，并生成了测试数据。

　　类的初始化代码（cs231n/classifiers/neural_net.py）：　　

   def __init__(self, input_size, hidden_size, output_size, std=1e-4):
     """
     Initialize the model. Weights are initialized to small random values and
     biases are initialized to zero. Weights and biases are stored in the
     variable self.params, which is a dictionary with the following keys:

     W1: First layer weights; has shape (D, H)
     b1: First layer biases; has shape (H,)
     W2: Second layer weights; has shape (H, C)
     b2: Second layer biases; has shape (C,)

     Inputs:
     - input_size: The dimension D of the input data.
     - hidden_size: The number of neurons H in the hidden layer.
     - output_size: The number of classes C.
     """
     self.params = {}
     self.params['W1'] = std * np.random.randn(input_size, hidden_size)
     self.params['b1'] = np.zeros(hidden_size)
     self.params['W2'] = std * np.random.randn(hidden_size, output_size)
     self.params['b2'] = np.zeros(output_size)

cell 3 前向传播计算loss，得到的结果与参考结果对比，证明模型的正确性：

 scores = net.loss(X)
 print 'Your scores:'
 print scores
 print
 print 'correct scores:'
 correct_scores = np.asarray([
   [-0.81233741, -1.27654624, -0.70335995],
   [-0.17129677, -1.18803311, -0.47310444],
   [-0.51590475, -1.01354314, -0.8504215 ],
   [-0.15419291, -0.48629638, -0.52901952],
   [-0.00618733, -0.12435261, -0.15226949]])
 print correct_scores

 # The difference should be very small. We get < 1e-7
 print 'Difference between your scores and correct scores:'
 print np.sum(np.abs(scores - correct_scores))

结果对比：

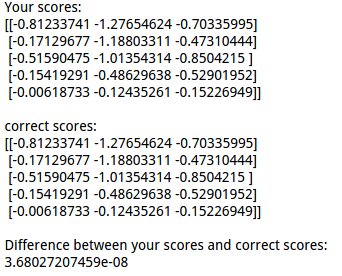
　　loss function 代码：

   def loss(self, X, y=None, reg=0.0):
     """
     Compute the loss and gradients for a two layer fully connected neural
     network.

     Inputs:
     - X: Input data of shape (N, D). Each X[i] is a training sample.
     - y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
       an integer in the range 0 <= y[i] < C. This parameter is optional; if it
       is not passed then we only return scores, and if it is passed then we
       instead return the loss and gradients.
     - reg: Regularization strength.

     Returns:
     If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
     the score for class c on input X[i].

     If y is not None, instead return a tuple of:
     - loss: Loss (data loss and regularization loss) for this batch of training
       samples.
     - grads: Dictionary mapping parameter names to gradients of those parameters
       with respect to the loss function; has the same keys as self.params.
     """
     # Unpack variables from the params dictionary
     W1, b1 = self.params['W1'], self.params['b1']
     W2, b2 = self.params['W2'], self.params['b2']
     #5 *4
     N, D = X.shape
     num_train = N
     # Compute the forward pass
     scores = None
     #############################################################################
     # TODO: Perform the forward pass, computing the class scores for the input. #
     # Store the result in the scores variable, which should be an array of      #
     # shape (N, C).                                                             #
     #############################################################################
     #5*4 * 4*10 >>>5*10
     buf_H = np.dot(X,W1) + b1
     #RELU
     buf_H[buf_H<0] = 0
     #5*10  * 10 *3 >>>5*3
     buf_O=np.dot(buf_H,W2) + b2
     scores = buf_O
     #############################################################################
     #                              END OF YOUR CODE                             #
     #############################################################################

     # If the targets are not given then jump out, we're done
     if y is None:
       return scores

     # Compute the loss
     loss = None
     #############################################################################
     # TODO: Finish the forward pass, and compute the loss. This should include  #
     # both the data loss and L2 regularization for W1 and W2. Store the result  #
     # in the variable loss, which should be a scalar. Use the Softmax           #
     # classifier loss. So that your results match ours, multiply the            #
     # regularization loss by 0.5                                                #
     #############################################################################
     scores = np.subtract( scores.T , np.max(scores , axis = 1) ).T
     scores = np.exp(scores)
     scores = np.divide( scores.T , np.sum(scores , axis = 1) ).T
     loss = - np.sum(np.log ( scores[np.arange(num_train),y] ) ) / num_train
     loss +=  0.5 * reg * (np.sum(W1*W1) + np.sum(W2*W2) )
     #############################################################################
     #                              END OF YOUR CODE                             #
     #############################################################################

     # Backward pass: compute gradients
     grads = {}
     #############################################################################
     # TODO: Compute the backward pass, computing the derivatives of the weights #
     # and biases. Store the results in the grads dictionary. For example,       #
     # grads['W1'] should store the gradient on W1, and be a matrix of same size #
     #############################################################################
     #get grad
     scores[np.arange(num_train),y]  -= 1
     # 10 *5  * 5*3 >>>10*3
     dW2 = np.dot(buf_H.T,scores)/num_train + reg*W2
     #
     db2 = np.sum(scores,axis =0)/num_train
     #10 * 3 * 3 *5 >>10 * 5
     buf_hide = np.dot(W2,scores.T)
     #element > 0
     buf_H[buf_H>0] = 1
     #relu buf_hide
     buf_relu = buf_hide.T * buf_H
     #4*5  * 5*10 >>4*10
     dW1 =   np.dot(X.T,buf_relu) /num_train + reg*W1
     #
     db1 = np.sum(buf_relu,axis =0) /num_train
     grads['W1'] = dW1
     grads['W2'] = dW2
     grads['b1'] = db1
     grads['b2'] = db2
     #############################################################################
     #                              END OF YOUR CODE                             #
     #############################################################################

     return loss, grads

cell 4  计算包含正则的loss

 loss, _ = net.loss(X, y, reg=0.1)
 correct_loss = 1.30378789133

 # should be very small, we get < 1e-12
 print loss
 print 'Difference between your loss and correct loss:'
 print np.sum(np.abs(loss - correct_loss))

结果：

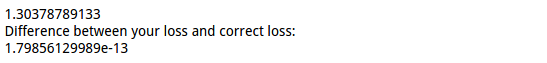
cell 5 反向传播，并用数值法来验证偏导的正确性》》注意使用链式法则：

 from cs231n.gradient_check import eval_numerical_gradient

 # Use numeric gradient checking to check your implementation of the backward pass.
 # If your implementation is correct, the difference between the numeric and
 # analytic gradients should be less than 1e-8 for each of W1, W2, b1, and b2.

 loss, grads = net.loss(X, y, reg=0.1)
 print  grads['W1'].shape
 print grads['W2'].shape
 print grads['b1'].shape
 print grads['b2'].shape
 # these should all be less than 1e-8 or so
 for param_name in grads:
   f = lambda W: net.loss(X, y, reg=0.1)[0]
   param_grad_num = eval_numerical_gradient(f, net.params[param_name], verbose=False)
   print '%s max relative error: %e' % (param_name, rel_error(param_grad_num, grads[param_name]))

显示解析法与数值法的结果差异：

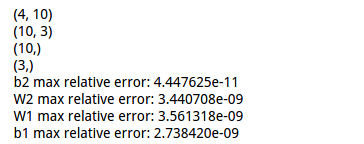
cell 6 训练网络模型。在loss grad 计算无误的基础上，使用对应的函数方法来训练模型。

 net = init_toy_model()
 #two layers net
 stats = net.train(X, y, X, y,
             learning_rate=1e-1, reg=1e-5,
             num_iters=100, verbose=False)

 print 'Final training loss: ', stats['loss_history'][-1]

 # plot the loss history
 plt.plot(stats['loss_history'])
 plt.xlabel('iteration')
 plt.ylabel('training loss')
 plt.title('Training Loss history')
 plt.show()

训练函数代码：

   def train(self, X, y, X_val, y_val,
             learning_rate=1e-3, learning_rate_decay=0.95,
             reg=1e-5, num_iters=100,
             batch_size=200, verbose=False):
     """
     Train this neural network using stochastic gradient descent.

     Inputs:
     - X: A numpy array of shape (N, D) giving training data.
     - y: A numpy array f shape (N,) giving training labels; y[i] = c means that
       X[i] has label c, where 0 <= c < C.
     - X_val: A numpy array of shape (N_val, D) giving validation data.
     - y_val: A numpy array of shape (N_val,) giving validation labels.
     - learning_rate: Scalar giving learning rate for optimization.
     - learning_rate_decay: Scalar giving factor used to decay the learning rate
       after each epoch.
     - reg: Scalar giving regularization strength.
     - num_iters: Number of steps to take when optimizing.
     - batch_size: Number of training examples to use per step.
     - verbose: boolean; if true print progress during optimization.
     """
     num_train = X.shape[0]
     iterations_per_epoch = max(num_train / batch_size, 1)

     # Use SGD to optimize the parameters in self.model
     loss_history = []
     train_acc_history = []
     val_acc_history = []

     for it in xrange(num_iters):
       X_batch = None
       y_batch = None

       #########################################################################
       # TODO: Create a random minibatch of training data and labels, storing  #
       # them in X_batch and y_batch respectively.                             #
       #########################################################################
       if batch_size > num_train:
         mask = np.random.choice(num_train, batch_size, replace=True)
       else :
         mask = np.random.choice(num_train, batch_size, replace=False)
       X_batch = X[mask]
       y_batch = y[mask]
       #########################################################################
       #                             END OF YOUR CODE                          #
       #########################################################################

       # Compute loss and gradients using the current minibatch
       loss, grads = self.loss(X_batch, y=y_batch, reg=reg)
       loss_history.append(loss)

       #########################################################################
       # TODO: Use the gradients in the grads dictionary to update the         #
       # parameters of the network (stored in the dictionary self.params)      #
       # using stochastic gradient descent. You'll need to use the gradients   #
       # stored in the grads dictionary defined above.                         #
       #########################################################################
       self.params['W1'] = self.params['W1'] - learning_rate * grads['W1']
       self.params['b1'] = self.params['b1'] - learning_rate * grads['b1']
       self.params['W2'] = self.params['W2'] - learning_rate * grads['W2']
       self.params['b2'] = self.params['b2'] - learning_rate * grads['b2']
       #########################################################################
       #                             END OF YOUR CODE                          #
       #########################################################################

       if verbose and it % 100 == 0:
         print 'iteration %d / %d: loss %f' % (it, num_iters, loss)

       # Every epoch, check train and val accuracy and decay learning rate.
       if it % iterations_per_epoch == 0:
         # Check accuracy
         train_acc = (self.predict(X_batch) == y_batch).mean()
         val_acc = (self.predict(X_val) == y_val).mean()
         train_acc_history.append(train_acc)
         val_acc_history.append(val_acc)

         # Decay learning rate
         learning_rate *= learning_rate_decay

     return {
       'loss_history': loss_history,
       'train_acc_history': train_acc_history,
       'val_acc_history': val_acc_history,
     }

显示最终的training loss以及绘制下降曲线：

之前都是使用比较简单的数据进行计算，接下来对cifar-10进行分类。

cell 7 载入训练和测试数据集，并显示各数据的维度：

 from cs231n.data_utils import load_CIFAR10

 def get_CIFAR10_data(num_training=49000, num_validation=1000, num_test=1000):
     """
     Load the CIFAR-10 dataset from disk and perform preprocessing to prepare
     it for the two-layer neural net classifier. These are the same steps as
     we used for the SVM, but condensed to a single function.
     """
     # Load the raw CIFAR-10 data
     cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
     X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)

     # Subsample the data
     mask = range(num_training, num_training + num_validation)
     X_val = X_train[mask]
     y_val = y_train[mask]
     mask = range(num_training)
     X_train = X_train[mask]
     y_train = y_train[mask]
     mask = range(num_test)
     X_test = X_test[mask]
     y_test = y_test[mask]

     # Normalize the data: subtract the mean image
     mean_image = np.mean(X_train, axis=0)
     X_train -= mean_image
     X_val -= mean_image
     X_test -= mean_image

     # Reshape data to rows
     X_train = X_train.reshape(num_training, -1)
     X_val = X_val.reshape(num_validation, -1)
     X_test = X_test.reshape(num_test, -1)

     return X_train, y_train, X_val, y_val, X_test, y_test

 # Invoke the above function to get our data.
 X_train, y_train, X_val, y_val, X_test, y_test = get_CIFAR10_data()
 print 'Train data shape: ', X_train.shape
 print 'Train labels shape: ', y_train.shape
 print 'Validation data shape: ', X_val.shape
 print 'Validation labels shape: ', y_val.shape
 print 'Test data shape: ', X_test.shape
 print 'Test labels shape: ', y_test.shape

结果显示：

cell 8 初始化网络并进行训练：

 input_size = 32 * 32 * 3
 hidden_size = 50
 num_classes = 10
 net = TwoLayerNet(input_size, hidden_size, num_classes)

 # Train the network
 stats = net.train(X_train, y_train, X_val, y_val,
             num_iters=1000, batch_size=200,
             learning_rate=1e-4, learning_rate_decay=0.95,
             reg=0.5, verbose=True)

 # Predict on the validation set
 val_acc = (net.predict(X_val) == y_val).mean()
 print 'Validation accuracy: ', val_acc

上述代码对验证集进行了预测，得到的准确率：

预测代码：

   def predict(self, X):
     """
     Use the trained weights of this two-layer network to predict labels for
     data points. For each data point we predict scores for each of the C
     classes, and assign each data point to the class with the highest score.

     Inputs:
     - X: A numpy array of shape (N, D) giving N D-dimensional data points to
       classify.

     Returns:
     - y_pred: A numpy array of shape (N,) giving predicted labels for each of
       the elements of X. For all i, y_pred[i] = c means that X[i] is predicted
       to have class c, where 0 <= c < C.
     """
     W1, b1 = self.params['W1'], self.params['b1']
     W2, b2 = self.params['W2'], self.params['b2']
     y_pred = None

     #5*10  * 10 *3 >>>5*3
     ###########################################################################
     # TODO: Implement this function; it should be VERY simple!                #
     ###########################################################################
     layer_hide = np.dot(X,W1) + b1
     layer_hide[layer_hide<0] = 0
     layer_soft = np.dot(layer_hide,W2) + b2
     scores = np.subtract( layer_soft.T , np.max(layer_soft , axis = 1) ).T
     scores = np.exp(scores)
     scores = np.divide( scores.T , np.sum(scores , axis = 1) ).T
     y_pred = np.argmax(scores , axis = 1)
     ###########################################################################
     #                              END OF YOUR CODE                           #
     ###########################################################################

     return y_pred

接下来，对网络模型进行一些调试，观察结果。

cell 9 绘制train集的loss以及train集的准确率与validation集的准确率：

 # Plot the loss function and train / validation accuracies
 plt.subplot(2, 1, 1)
 plt.plot(stats['loss_history'])
 plt.title('Loss history')
 plt.xlabel('Iteration')
 plt.ylabel('Loss')

 plt.subplot(2, 1, 2)
 plt.plot(stats['train_acc_history'], label='train')
 plt.plot(stats['val_acc_history'], label='val')
 plt.title('Classification accuracy history')
 plt.xlabel('Epoch')
 plt.ylabel('Clasification accuracy')
 plt.show()

绘制的图形曲线：

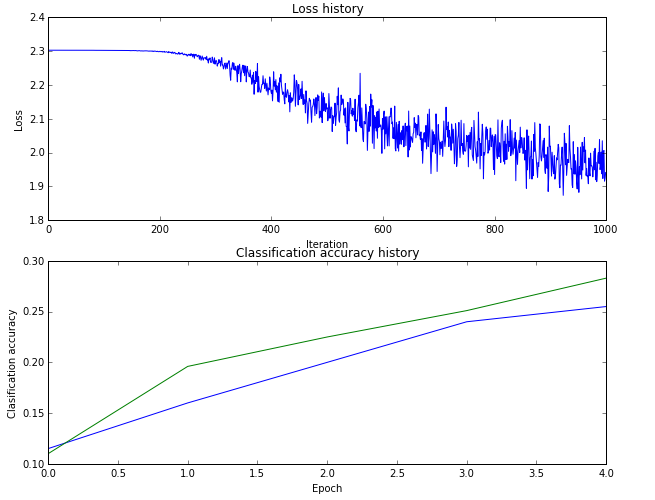
cell 10 对w的分量分别进行可视化：

 from cs231n.vis_utils import visualize_grid

 # Visualize the weights of the network

 def show_net_weights(net):
   W1 = net.params['W1']
   W1 = W1.reshape(32, 32, 3, -1).transpose(3, 0, 1, 2)
   plt.imshow(visualize_grid(W1, padding=3).astype('uint8'))
   plt.gca().axis('off')
   plt.show()

 show_net_weights(net)

结果：

接着是通过验证的方式选取超参数，包括：隐藏层的结点数、学习率、正则化强度系数。

cell 11 选取超参数，没有对正则化强度系数及其衰减系数进行选取：

 best_net = None # store the best model into this
 best_val = 0
 #################################################################################
 # TODO: Tune hyperparameters using the validation set. Store your best trained  #
 # model in best_net.                                                            #
 #                                                                               #
 # To help debug your network, it may help to use visualizations similar to the  #
 # ones we used above; these visualizations will have significant qualitative    #
 # differences from the ones we saw above for the poorly tuned network.          #
 #                                                                               #
 # Tweaking hyperparameters by hand can be fun, but you might find it useful to  #
 # write code to sweep through possible combinations of hyperparameters          #
 # automatically like we did on the previous exercises.                          #
 #################################################################################
 input_size = 32 * 32 * 3
 Hidden_size = [50 ,64,128]
 REG = [0.01,0.1,0.5]
 num_classes = 10
 for i in Hidden_size:
     for j in REG :
       net = TwoLayerNet(input_size,  i, num_classes)
 # Train the network
       stats = net.train(X_train, y_train, X_val, y_val,
                     num_iters=2000, batch_size=200,
                     learning_rate=1e-3, learning_rate_decay=0.95,
                     reg = j, verbose=False)
       val_acc = (net.predict(X_val) == y_val).mean()
       print 'Validation accuracy: ', val_acc
       if best_val < val_acc:
         best_val = val_acc
         best_net = net
 #################################################################################
 #                               END OF YOUR CODE                                #
 #################################################################################

显示各个参数的验证集准确率结果：

cell 12 可视化最优参数对应模型的隐藏层结点对应的w的结果:

 # visualize the weights of the best network
 show_net_weights(best_net)

结果：

cell 13 使用最优参数模型对测试集进行预测：

 test_acc = (best_net.predict(X_test) == y_test).mean()
 print 'Test accuracy: ', test_acc

得到的结果：

附：通关CS231n企鹅群：578975100 validation：DL-CS231n