NOIP2017整数 【线段树】

题目

题目背景

在人类智慧的山巅，有着一台字长为10485761048576 位（此数字与解题无关）的超级计算机，著名理论计算机科

学家P博士正用它进行各种研究。不幸的是，这天台风切断了电力系统，超级计算机

无法工作，而 P 博士明天就要交实验结果了，只好求助于学过OI的你. . . . . .

题目描述

P 博士将他的计算任务抽象为对一个整数的操作。

具体来说，有一个整数xx ，一开始为00 。

接下来有nn 个操作，每个操作都是以下两种类型中的一种：

1 a b：将xx 加上整数a\cdot 2^ba⋅2

b

，其中aa 为一个整数，bb 为一个非负整数

2 k ：询问xx 在用二进制表示时，位权为2^k2

k

的位的值（即这一位上的11 代表 2^k2

k

）

保证在任何时候，x\geqslant 0x⩾0 。

输入格式

输入的第一行包含四个正整数n,t_1,t_2,t_3n,t

1

​ ,t

2

​ ,t

3

​ ，nn 的含义见题目描述，t_1t

1

​ ，t_2t

2

​ ，t_3t

3

​ 的具体含义见子任务。

接下来nn 行，每行给出一个操作，具体格式和含义见题目描述。

同一行输入的相邻两个元素之间，用恰好一个空格隔开。

输出格式

对于每个询问操作，输出一行，表示该询问的答案（00 或11 ）。对于加法操作，没有任何输出。

输入样例

10 3 1 2

1 100 0

1 2333 0

1 -233 0

2 5

2 7

2 15

1 5 15

2 15

1 -1 12

2 15

输出样例

0

1

0

1

0

提示

在所有测试点中，1\leqslant t_1 \leqslant 3, 1 \leqslant t_2 \leqslant 4, 1 \leqslant t_3 \leqslant 21⩽t

1

​ ⩽3,1⩽t

2

​ ⩽4,1⩽t

3

​ ⩽2 。不同的 t_1, t_2, t_3t

1

​ ,t

2

​ ,t

3

​ 对应的特殊限制如下：

对于 t_1 = 1t

1

​ =1 的测试点，满足 a = 1a=1

对于 t_1 = 2t

1

​ =2 的测试点，满足 |a| = 1∣a∣=1

对于 t_1 = 3t

1

​ =3 的测试点，满足 |a| \leqslant 10^9∣a∣⩽10

9

对于 t_2 = 1t

2

​ =1 的测试点，满足 0 \leqslant b, k \leqslant 300⩽b,k⩽30

对于 t_2 = 2t

2

​ =2 的测试点，满足 0 \leqslant b, k \leqslant 1000⩽b,k⩽100

对于 t_2 = 3t

2

​ =3 的测试点，满足 0 \leqslant b, k \leqslant n0⩽b,k⩽n

对于 t_2 = 4t

2

​ =4 的测试点，满足 0 \leqslant b, k \leqslant 30n0⩽b,k⩽30n

对于 t_3 = 1t

3

​ =1 的测试点，保证所有询问操作都在所有修改操作之后

对于 t_3 = 2t

3

​ =2 的测试点，不保证询问操作和修改操作的先后顺序

本题共 25 个测试点，每个测试点 4 分。各个测试点的数据范围如下：

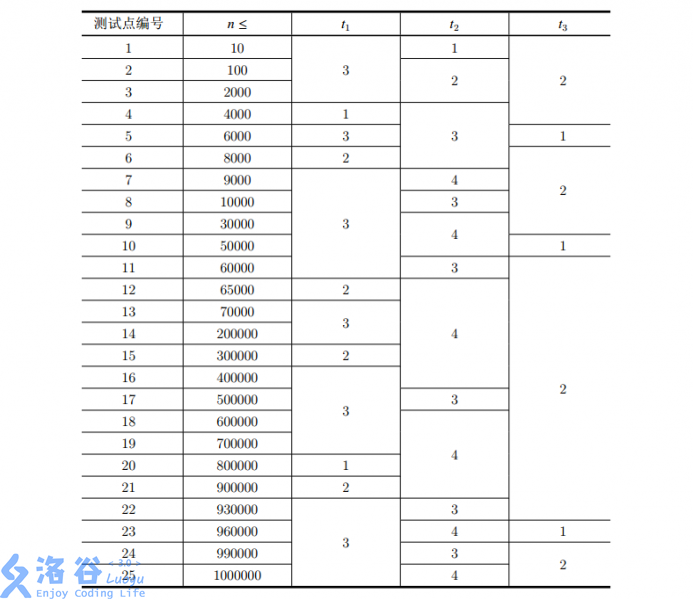
题解

先考虑暴力

我们将30位压在一起，存到一个数组中，每次加减只要找到对应位置加上，处理进位即可

但这样会T，因为进位可以是一整个数组

什么情况下会T呢？

考虑11111111111111111111111111111111111111......

我们加上一个1

变成10000000000000000000000000000000000.....

又减去一个1

变成1111111111111111111111111111111111111111.....

我们发现，如果进位的地方不是全1，可以直接加上

如果进位的地方全1，那么重置为0，往下一位继续进位

如果有一整段都为1，那么全部置为0，往第一个不全是1的位进1

所以可以写一个线段树维护

【口胡很简单。。。。。我不会说我调了一个下午】

#include<iostream>
#include<cstdio>
#include<algorithm>
#define BIT (1 << 30)
#define ls (u << 1)
#define rs (u << 1 | 1)
#define LL long long int
using namespace std;
const int maxn = 1000005,maxm = 1000005,INF = BIT - 1;
inline LL read(){
	LL out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57) {out = (out << 3) + (out << 1) + c - '0'; c = getchar();}
	return out * flag;
}
LL n,val[4 * maxn],tag[4 * maxn];
void pd(int u){
	if (tag[u] == -1) val[ls] = val[rs] = 0,tag[ls] = tag[rs] = -1;
	if (tag[u] == 1) val[ls] = val[rs] = INF,tag[ls] = tag[rs] = 1;
	tag[u] = 0;
}
void upd(int u){
	if (val[ls] == INF && val[rs] == INF) val[u] = INF;
	else if (val[ls] == 0 && val[rs] == 0) val[u] = 0;
	else val[u] = 1;
}
int modify(int u,int l,int r,int pos,LL v){
	if (l == r){
		val[u] += v;
		if (val[u] < 0) {val[u] += BIT; return -1;}
		if (val[u] > INF) {val[u] -= BIT; return 1;}
		return 0;
	}
	pd(u);
	int mid = l + r >> 1,t;
	if (mid >= pos) t = modify(ls,l,mid,pos,v);
	else t = modify(rs,mid + 1,r,pos,v);
	upd(u);
	return t;
}
int Add(int u,int l,int r,int pos){
	if (l == r){
		val[u]++;
		if (val[u] > INF) {val[u] = 0; return true;}
		return false;
	}
	pd(u);
	int mid = l + r >> 1,t = true;
	if (l >= pos){
		if (val[ls] == INF){
			val[ls] = 0; tag[ls] = -1;
			t = Add(rs,mid + 1,r,pos); upd(u);
			return t;
		}
		t = Add(ls,l,mid,pos); upd(u);
		return t;
	}
	if (mid >= pos) t = Add(ls,l,mid,pos);
	if (t) t = Add(rs,mid + 1,r,pos);
	upd(u);
	return t;
}
int Minus(int u,int l,int r,int pos){
	if (l == r){
		val[u]--;
		if (val[u] < 0) {val[u] = INF; return true;}
		return false;
	}
	pd(u);
	int mid = l + r >> 1,t = true;
	if (l >= pos){
		if (val[ls] == 0){
			val[ls] = INF; tag[ls] = 1;
			t = Minus(rs,mid + 1,r,pos); upd(u);
			return t;
		}
		t = Minus(ls,l,mid,pos); upd(u);
		return t;
	}
	if (mid >= pos) t = Minus(ls,l,mid,pos);
	if (t) t = Minus(rs,mid + 1,r,pos);
	upd(u);
	return t;
}
int getv(int u,int l,int r,int pos,LL v){
	if (l == r) return (val[u] & (1 << v)) != 0;
	pd(u);
	int mid = l + r >> 1;
	if (mid >= pos) return getv(ls,l,mid,pos,v);
	return getv(rs,mid + 1,r,pos,v);
}
int main(){
	n = read(); read(); read(); read();
	int opt,a,b,t,pos,tt,len,flag;
	for (int i = 1; i <= n; i++){
		opt = read(); a = read();
		if (opt & 1){
			b = read(); flag = a >= 0 ? 1 : -1;
			a *= flag;
			pos = b / 30; tt = b - pos * 30; len = 30 - tt;
			t = modify(1,0,n + 5,pos,flag * ((a & ((1 << len) - 1)) << tt));
			if (t == 1) Add(1,0,n + 5,pos + 1);
			if (t == -1) Minus(1,0,n + 5,pos + 1);
			a >>= len;
			if (a){
				t = modify(1,0,n + 5,pos + 1,flag * a);
				if (t == 1) Add(1,0,n + 5,pos + 2);
				if (t == -1) Minus(1,0,n + 5,pos + 2);
			}
		}else {
			printf("%d\n",getv(1,0,n + 5,a / 30,a % 30));
		}
	}
	return 0;
}