剑指Offer：矩形覆盖【N1】

剑指Offer：矩形覆盖【N1】

题目描述

　　我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

题目思考

　　大矩形是由单元块（1*2）填充的，但是大矩形不是一下生成的，而是由比他小的矩形通过添加单元块生成的，添加的策略只能是两种

• 第一，小矩形右侧添加竖状单元块，要求，小矩形比大矩形小一个单位。
• 第二，小矩形右侧添加横状单元块，要求，小矩形比大矩形少两个单位。

　　这依然是斐波那契数列变形题，经典的动态规划题目，按照斐波那契数列特点求解，每个子问题，即不同长度的小矩形方法数，求解一次，存在存储表中，下次遇到后直接取用即可。

　　

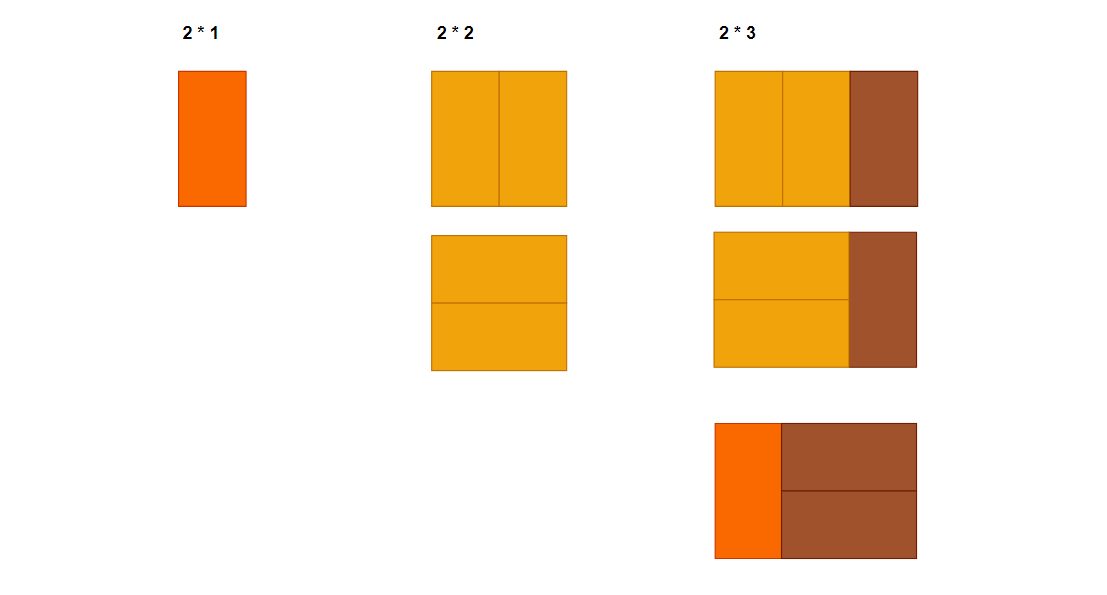
Java题解

public class RectCover {
    public static int RectCover(int n) {
        if (n <= 2)
            return n;
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i < n; i++)
            dp[i] = dp[i - 1] + dp[i - 2];
        return dp[n - 1];
    }

    public static void main(String[] args) {
        System.out.println(RectCover(3));
    }
}