POJ 3895 Cycles of Lanes (dfs)

Description

Each of the M lanes of the Park of Polytechnic University of Bucharest connects two of the N crossroads of the park (labeled from 1 to N). There is no pair of crossroads connected by more than one lane and it is possible to pass from each crossroad to each
other crossroad by a path composed of one or more lanes. A cycle of lanes is simple when passes through each of its crossroads exactly once. 

The administration of the University would like to put on the lanes pictures of the winners of Regional Collegiate Programming Contest in such way that the pictures of winners from the same university to be on the lanes of a same simple cycle. That is why the
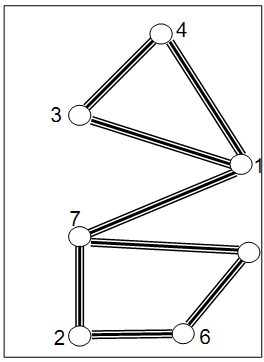
administration would like to assign the longest simple cycles of lanes to most successful universities. The problem is to find the longest cycles? Fortunately, it happens that each lane of the park is participating in no more than one simple cycle (see the
Figure). 

Input

On the first line of the input file the number T of the test cases will be given. Each test case starts with a line with the positive integers N and M, separated by interval (4 <= N <= 4444). Each of the next M lines of the test case contains the labels of
one of the pairs of crossroads connected by a lane.

Output

For each of the test cases, on a single line of the output, print the length of a maximal simple cycle.

Sample Input

1
7 8
3 4
1 4
1 3
7 1
2 7
7 5
5 6
6 2

Sample Output

4

Source

Southeastern European Regional Programming Contest 2009

题意就是求最大的环包括点的个数。可是有一个麻烦的地方。就是dfs 到一个点时，怎么高速知道与这个点相连点呢？

后来我知道了 vector 开一个vector数组保存即可了。接下来就是代码了，细节在代码中

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
#define N 5000

vector<int>q[N];

int vis[N];
int n,m;
int ans;

void dfs(int a,int pos)
{
    int i;
    vis[a]=pos;

    for(i=0;i<q[a].size();i++)
     {
         int x=q[a][i];

         if(!vis[x])
            dfs(x,pos+1);
         else
            if(vis[a]-vis[x]+1>ans)  //比如环 1 2 3 4 1 ,vis[1]=1,vis[4]=4,下一次4与
                                    //1相连。可是已经vis[1],所以环的大小 vis[4]-vis[1]+1
               ans=vis[a]-vis[x]+1;
     }
}

int main()
{
    int i,t;
    scanf("%d",&t);

    while(t--)
    {
        scanf("%d%d",&n,&m);
        memset(vis,0,sizeof(vis));
        int x,y;

        for(i=1;i<=n;i++)  //记得清空上次的数据
            q[i].clear();

        while(m--)
        {
            scanf("%d%d",&x,&y);
            q[x].push_back(y);  //q[x]存与x的临边
            q[y].push_back(x);  //同理
        }

        ans=0;
       for(i=1;i<=n;i++)
        if(!vis[i])  //由于一个点就会出现一次。即使两个环有共同边，
                     //那么在公共边那个分叉点还是会分别进行dfs的
            dfs(i,1);
                    //不加以下会错
        if(ans<=2)//一个环须要3个点。可是我郁闷了。假设没有环的话
                  //怎么会有vis[x]已经标记了呢？（此时ans=0啊）难道有数据相似
                  // a b   b a  (⊙o⊙)…
            ans=0;
        printf("%d\n",ans);
    }
    return 0;
}

dfs还不是非常熟，可是有事缠身。哎以后一定好好补补dfs

今天听说一种叫做邻接表的东西，竟然用一维数组存储与随意起点相关联的全部边的信息，感觉非常奇妙，不怎么好懂，刚刚入门o(╯□╰)o，也能够用到这个提上

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 4500

int ans,vis[N],head[N];
int n,m,num;

struct stud{
int to,next;
}e[N*2];

void build(int u,int v)
{
    e[num].to=v;
    e[num].next=head[u];
    head[u]=num;
    num++;
}

void dfs(int x,int pos)
{
    vis[x]=pos;
    int i;

    for(i=head[x];i!=-1;i=e[i].next)
    {
        if(vis[e[i].to])
            ans=max(ans,vis[x]-vis[e[i].to]+1);
        else
            dfs(e[i].to,pos+1);
    }
}
int main()
{
    int i,j,v,u,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        memset(head,-1,sizeof(head));

        num=0;
        while(m--)
        {
            scanf("%d%d",&v,&u);
            build(v,u);
            build(u,v);
        }
        memset(vis,0,sizeof(vis));
        ans=0;

        dfs(1,0);

        if(ans<3) ans=0;

        printf("%d\n",ans);
    }
    return 0;
}