「LuoguP4147」 玉蟾宫（并查集

题目背景

有一天，小猫rainbow和freda来到了湘西张家界的天门山玉蟾宫，玉蟾宫宫主蓝兔盛情地款待了它们，并赐予它们一片土地。

题目描述

这片土地被分成N*M个格子，每个格子里写着'R'或者'F'，R代表这块土地被赐予了rainbow，F代表这块土地被赐予了freda。

现在freda要在这里卖萌。。。它要找一块矩形土地，要求这片土地都标着'F'并且面积最大。

但是rainbow和freda的OI水平都弱爆了，找不出这块土地，而蓝兔也想看freda卖萌（她显然是不会编程的……），所以它们决定，如果你找到的土地面积为S，它们每人给你S两银子。

输入输出格式

输入格式：

第一行两个整数N,M，表示矩形土地有N行M列。

接下来N行，每行M个用空格隔开的字符'F'或'R'，描述了矩形土地。

输出格式：

输出一个整数，表示你能得到多少银子，即(3*最大'F'矩形土地面积)的值。

输入输出样例

输入样例#1：
复制

5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F

输出样例#1： 复制

45

说明

对于50%的数据，1<=N,M<=200

对于100%的数据，1<=N,M<=1000

题解

这是来自我校学长(祖传)的并查集做法

首先从上到下枚举每一行（分割线）。

在当前行，把它以上的F染色，那么F会构成这样的图案↓

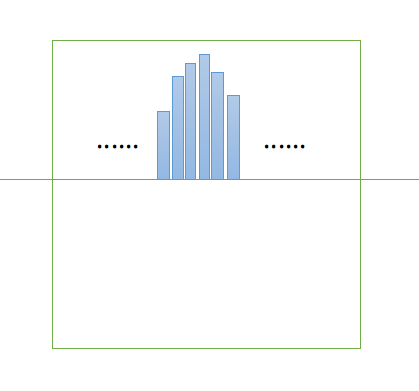
每一列在这条分割线以上有多少连续的F，可以在每次下移分割线时顺便用O(m)扫一遍维护。（如果这一格为F，那么连续F为之前这列的连续F加1;否则为0）

然后我们按照每一列的F高度排序，每次把F最高的取出来。

如果它左边一列被取过了，我们就把当前列和它左边一列并起来;如果右边一列被取过，就把这一列和右边一列并起来。

最后询问一下这一列的祖先有多少个子节点，也就是这一列以它的高度往左右最多能扩展的宽度。

原理：在当前列之前被并入这个祖先的列的长度一定大于等于当前列的长度，并且这些列互相相邻。

然后当前列的高度，乘上它往左右最多能扩展的宽度，就是取这一列，且高度等于这一列的最大矩形面积了。(就算还有相同高度的没有处理，之后做那一列的时候也会得到最优解)

实现的时候只需要把两个需要合并的列的祖先节点$fa[v]=u,siz[u]+=siz[v]$就可以了，因为只有祖先节点的siz是有意义的。

因为懒所以直接用了优先队列，并查集只路径压缩也是$O(mlogm)$的时间，总复杂度$O(nmlogm)$

 /*
     qwerta
     P4147 玉蟾宫
     Accepted
     100
     代码 C++，1.14KB
     提交时间 2018-10-14 22:07:46
     耗时/内存
     1724ms, 916KB
 */
 #include<iostream>
 #include<cstdio>
 #include<queue>
 using namespace std;
 int s[];//记录每列往上F的高度
 int fa[],siz[];//并查集
 bool sf[];//标记每一列是否被用过
 struct emm{
     int nod,v;
 };
 struct cmp{
     bool operator()(emm qaq,emm qwq){
         return qaq.v<qwq.v;
     }
 };//重载()运算符（用来给优先队列排序
 priority_queue<emm,vector<emm>,cmp>q;
 int fifa(int x)
 {
     if(fa[x]==x)return x;
     return fa[x]=fifa(fa[x]);
 }
 void con(int x,int y)//把x列和y列并起来
 {
     int u=fifa(x),v=fifa(y);
     fa[v]=u;
     siz[u]+=siz[v];
     return;
 }
 int main()
 {
     //freopen("a.in","r",stdin);
     ios::sync_with_stdio(false);
     cin.tie(false),cout.tie(false);//关闭同步流（让cin变快
     int n,m;
     cin>>n>>m;
     int ans=;
     for(int c=;c<=n;++c)//从上往下移分割线
     {
         for(int i=;i<=m;++i)
         {
             char ch;
             cin>>ch;
             if(ch=='F'){s[i]++;q.push((emm){i,s[i]});}
             else s[i]=;
         }
         for(int i=;i<=m;++i)
         fa[i]=i,siz[i]=,sf[i]=;//初始化
         while(!q.empty())
         {
             int i=q.top().nod,x=q.top().v;q.pop();
             sf[i]=;//标记这一列取过了
             if(sf[i-])con(i-,i);//如果左边取过了就并起来
             if(sf[i+])con(i,i+);//如果右边取过了就并起来
             int fi=fifa(i);//找祖先节点
             ans=max(ans,siz[fi]*x);
         }
     }
     cout<<ans*;//输出最大矩形面积*3
     return ;
 }