1568: [JSOI2008]Blue Mary开公司（超哥线段树）

1568: [JSOI2008]Blue Mary开公司

Time Limit: 15 Sec  Memory Limit: 162 MB
Submit: 1198  Solved: 418

Description

Input

第一行 ：一个整数N ，表示方案和询问的总数。 

接下来N行，每行开头一个单词“Query”或“Project”。 

若单词为Query，则后接一个整数T，表示Blue Mary询问第T天的最大收益。 

若单词为Project，则后接两个实数S，P，表示该种设计方案第一天的收益S，以及以后每天比上一天多出的收益P。

1 <= N <= 100000 1 <= T <=50000 0 < P < 100，| S | <= 10^6 

提示：本题读写数据量可能相当巨大，请选手注意选择高效的文件读写方式。

Output

对于每一个Query，输出一个整数，表示询问的答案，并精确到整百元（以百元为单位，

例如：该天最大收益为210或290时，均应该输出2）。没有方案时回答询问要输出0

Sample Input

10
Project 5.10200 0.65000
Project 2.76200 1.43000
Query 4
Query 2
Project 3.80200 1.17000
Query 2
Query 3
Query 1
Project 4.58200 0.91000
Project 5.36200 0.39000

Sample Output

0
0
0
0
0

HINT

 

Source

分析

超哥线段树，记录每个点的最大的线段是谁。查询时用这条线段查询。

那么怎么记录呢，（当时这个问题困惑我好久），线段树只能记录一段区间，对于一条线段它只记录一段区间，怎么保存区间所有的线段？

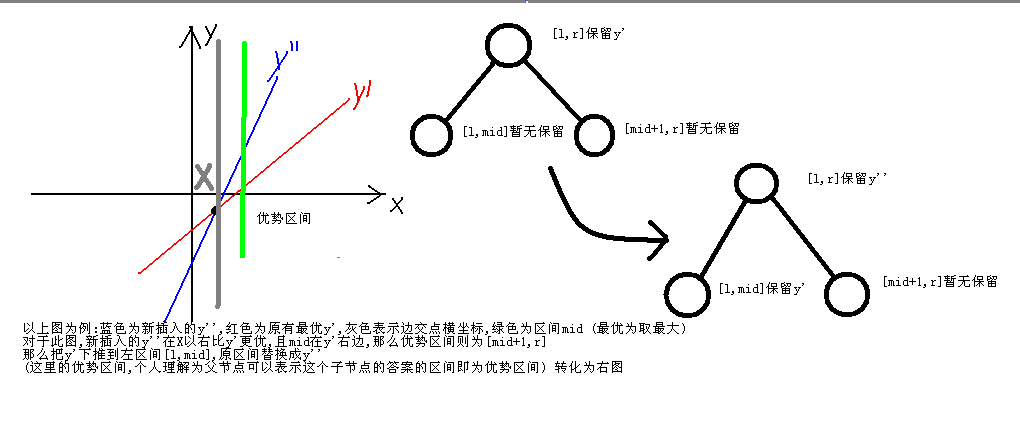
借用一张图说明这一点。

对于原来的区间[l,r]表示y'这条线段，就是让[l,r]区间的所有的线段是y'，然后来了一条线段y”，显然在x点右边，y”要比y’更优，但是线段树只能从中间劈开，不能[l,x][x,r]这样，所以我们就找到中点mid = (l+r)/2，这样[mid,r]这段区间可以直接更新了，左区间继续像这样分，全部都更新完就好了。

code

 #include<cstdio>
 #include<algorithm>
 #define lson l,m,rt<<1
 #define rson m+1,r,rt<<1|1

 using namespace std;

 const int MAXN = ;
 int fut[MAXN<<];
 double a[MAXN<<],b[MAXN<<];
 char opt[];
 int tot;

 int pd(int x,int y,int p)
 {
     return a[x]+(p-)*b[x] > a[y]+(p-)*b[y];
 }
 void update(int l,int r,int rt,int x)
 {
     if (l==r)
     {
         if (pd(x,fut[rt],l)) fut[rt] = x;
         return ;
     }
     int m = (l+r)>>;
     if (b[x]>b[fut[rt]])
     {
         if (pd(x,fut[rt],m)) update(lson,fut[rt]), fut[rt] = x;
         else update(rson,x);
     }
     if (b[x]<b[fut[rt]])
     {
         if (pd(x,fut[rt],m)) update(rson,fut[rt]), fut[rt] = x;
         else update(lson,x);
     }
 }
 double getans(int k,int x)
 {
     return a[k]+(x-)*b[k];
 }
 double query(int l,int r,int rt,int x)
 {
     if (l==r) return getans(fut[rt],x);
     int m = (l+r)>>;
     double ans = getans(fut[rt],x);
     if (x<=m) ans = max(ans,query(lson,x));
     else ans = max(ans,query(rson,x));
     return ans;
 }
 int main()
 {
     int n,x;
     scanf("%d",&n);
     for (int i=; i<=n; ++i)
     {
         scanf("%s",opt);
         if (opt[]=='P')
         {
             ++tot;
             scanf("%lf%lf",&a[tot],&b[tot]);
             update(,n,,tot);
         }
         else
         {
             scanf("%d",&x);
             double t1 = query(,n,,x);
             int t2 = t1;
             printf("%d\n",t2/);
         }
     }
     return ;
 }