PCA本质和SVD

一、一些概念

线性相关：其中一个向量可以由其他向量线性表出。

线性无关：其中一个向量不可以由其他向量线性表出，或者另一种说法是找不到一个X不等于0，能够使得AX=0。如果对于一个矩阵A来说它的列是线性无关的，则AX=0，只有0解，此时矩阵A可逆。

秩：线性无关向量个数。

基：

特征向量：向量X经过矩阵A旋转后，与原来的X共线，。即为特征值，表示向量的伸缩。如果把矩阵看成进行线性变化的矩阵（旋转，拉伸），那么特征向量就是这样一种向量，它经过这种特定的变换后保持方向不变，只是进行长度上的伸缩而已。反过来，特征向量组成的正交底恰恰也是一种变换，将矩阵从一个空间映射到另一个空间。

特征分解：

如果矩阵A是对称矩阵，那会得到一个更强的特征分解，A可实现U对角化，即正交对角化。特征向量U正交：

二、PCA的本质（协方差矩阵对角化，对称矩阵特征分解）

数据量太大的时候，需要降维。怎么降呢？需要保证维度减少，但同时信息量保留的最多，转换成数学术语就是每个行向量的方差尽可能大（方差代表信息），行向量间的协方差为0（让行与行之间尽量不相关，信息尽量转移到某几个单独的变量上，从而实现降维）。下面以矩阵X为例进行讲解，假设拿到的数据是矩阵X ,

它的协方差矩阵则为（标准化数据以后）：

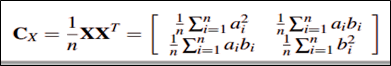
有两步需要做1.现在希望的是降维后的协方差矩阵对角元尽可能大（信息量足够多），非对角元尽可能为0（行与行之间无关，如果相关说明没有降维成功），即变成一个对角矩阵。因此我们需要对X做一个线性变换，使得做线性变换后的矩阵的协方差矩阵变成对角矩阵（相当于变化新的坐标）。而怎么线性变换呢？具体如下图，使得Q=U^t时，Cy就会变成一个对角矩阵，这时候需要用到前面的特征值分解，因为Cx是对称矩阵，所以可以进行特征分解：

2.Cy变成对角矩阵后，我们如何降维呢？此时需要将对角元上的特征值进行排序，此时可以把特征值小的那部分对应的信息丢掉，此时就达到了降维的目的。特征值此时代表的就是信息量的大小。具体如下图中的例子：

Python中用到的代码：

http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html

pca就是寻找协方差矩阵的特征值，特征向量，找到方向最大的变异方向（特征向量），再找到跟它正交的，如此下去找到n个主成分。需要先标准化，因为是通过最大化线性组合方差得到，所以对变量的测量尺度敏感。

三、SVD分解（奇异矩阵分解）

前面讲到的对称矩阵的分解才能实现正交对角化(U^T=U^-)，而对称矩阵是建立在R^n*n的空间，而对于任意秩为R的矩阵A属于R^m*n的空间时，能不能找到类似的分解呢？答案是可以滴，这就是SVD分解了, 为奇异值，且大于0。

SVD与特征分解有没有什么关系呢？

奇异值就是A*A^T非零的特征值开根号。在PCA应用中，协方差矩阵是正定矩阵，而正定矩阵（一定是对称矩阵）的奇异分解实质等价于特征分解。

SVD同样可以进行降维。