nlopt 二次优化

/*
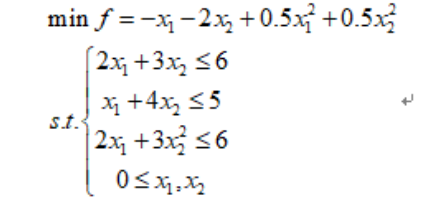
* main.c
*
*  Created on: Oct 9, 2018
*      Author: lgh
*/
 
#include <stdio.h>
#include <math.h>
#include "nlopt.h"
#define INF 1e10
int i = ;
 
double step = ;
 
//目标函数；
double utility(unsigned n, const double *x, double *grad, void *data)
{
    if (grad) {
        grad[] = (-1.0 + x[])*step;
        grad[] = (-2.0 + x[])*step;
    }
    printf("迭代次数 i= %d, x[0]=%f, x[1]= %f，f(x1,x2)=%f\n",
        i++, x[], x[], -x[] -  * x[] + 0.5*x[] * x[] + 0.5*x[] * x[]);
    return (-x[] -  * x[] + 0.5*x[] * x[] + 0.5*x[] * x[]);
}
 
//不等式限制条件；
double inconstraint_1(unsigned n, const double *x, double *grad, void *data)
{
    if (grad) {
        grad[] = 2.0*step;
        grad[] = 3.0*step;
    }
    return ( * x[] +  * x[] - );
}
 
//不等式限制条件；
double inconstraint_2(unsigned n, const double *x, double *grad, void *data)
{
    if (grad) {
        grad[] = 1.0*step;
        grad[] = 4.0*step;
    }
    return (x[] +  * x[] - );
}
 
//不等式限制条件；
double inconstraint_3(unsigned n, const double *x, double *grad, void *data)
{
    if (grad) {
        grad[] = 2.0*step;
        grad[] = 6.0*x[] * step;
    }
    return ( * x[] +  * x[] * x[] - );
}
 
int main(int argc, char const *argv[])
{
    double tol = 1e-;
    double lb[] = { , };       //x1、x2的下边界；
    double ub[] = { INF,INF };
    double x[] = { ,  };      //给x1、x2赋予初始值；
    double f_min;
 
    nlopt_opt opter = nlopt_create(NLOPT_LD_SLSQP/*NLOPT_LD_MMA*/, );
 
    //设置自变量下限；
    nlopt_set_lower_bounds(opter, lb);
 
    // 目标函数；
    nlopt_set_min_objective(opter, utility, NULL);
 
    // 不等式约束；
    nlopt_add_inequality_constraint(opter, inconstraint_1, NULL, tol);
    nlopt_add_inequality_constraint(opter, inconstraint_2, NULL, tol);
    nlopt_add_inequality_constraint(opter, inconstraint_3, NULL, tol);
 
    // 停止时需要的条件；
    nlopt_set_xtol_rel(opter, tol);
 
    // 开始优化；
    nlopt_result result = nlopt_optimize(opter, x, &f_min);
 
    if (result)
    {
        printf("极小值=%g, x=(%g,%g)\n", f_min, x[], x[]);
    }
 
    //free
    nlopt_destroy(opter);
    getchar();
    return ;
}