使用帅气的cordic算法进行坐标系互转及log10的求解
参考博客
https://blog.csdn.net/u010712012/article/details/77755567
https://blog.csdn.net/Reborn_Lee/article/details/87436090
参考论文
基于FPGA的自然对数变换器的设计与实现.pdf
前言
众所周知，verilog并不能直接计算cos sin，但信号处理中却可能用到cos sin等函数的求解问题。
一种足够好的逼近方式为cordic。无需使用乘法操作，只是简单的加减移位操作即可，这就可以很好的使用verilog操作啦。
cordic算法有旋转模式和向量模式两种，分别可在圆坐标系、线性坐标系、双曲坐标系中使用。
在旋转模式中，通过使Z逼近0，得到x,y。
在向量模式中，通过使y逼近0，得到x,z。
线性坐标系暂时没有用到。
通过给定不同的初值，则可以求解不同的函数。
极坐标转直角坐标
已知（z,r）,z表示角度，r表示极径。则可以通过旋转模式求解cos,sin。再乘r则得到实际上的直角坐标系（x,y）。
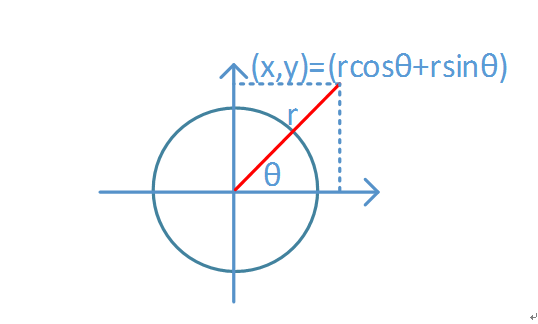
算法流程：本次迭代次数为16次，其他次数照着迭代公式写即可，为方便fpga内部计算，数值均放大成整数，角度均放大了2^16次，则计算出来的最终结果也应相应除以2^16次。
1、 设置迭代次数为16，则x0 = 0.607253，y0 = 0，并输入待计算的角度θ，θ在[-99.7°，99.7°]范围内。
2、 根据三个迭代公式进行迭代，i从0至15：
xi+1 = xi – d iy i2-i
yi+1 = yi + d ix i2-i
zi+1 = zi - diθi
注：z0 = θ，di与zi同符号。
3、 经过16次迭代计算后，得到的x16 和y16分别为cosθ和sinθ。
计算出的cos和sin再乘r即可得到相应的直角坐标系点（x,y）。
算法的本质即从45度开始旋转，直到z逼近0。而算法中的K本质上是个定值跟迭代次数有关，即∏cosθi。当迭代16次时，其值为
0.6072529351。
以下采用流水线对算法进行实现，可以获得最大的吞吐率。如果想节约资源，自然可以用复用串行迭代。
原始cordic可以处理的角度范围为[-99.7°，99.7°]，要想放大输入角度范围覆盖[-pi,pi]，则需要前处理和后处理，使得角度处于第1和第4象限。
仿真结果如下所示：
角度输入为33度，则结果为：cos：54959/2^16=0.838607788085938 ,sin:35697/2^16= 0.544692993164063
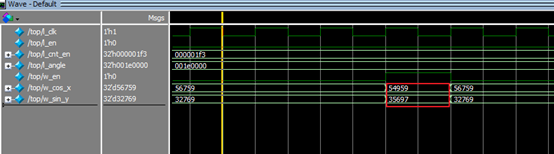
而matlab结果为：cos: 0.838670567945424 , sin: 0.544639035015027
可以看到误差极小。
代码仅供参考，勿做商业用途。
`timescale 1ns/1ps
module cos_sin_cordic (
input i_clk ,
input i_en ,
input signed [:] i_angle ,
output o_en ,
output o_error ,
output [:] o_cos_x ,
output [:] o_sin_y
);
////parameter
parameter p_angle_0 = , //45°放大2^16
p_angle_1 = ,
p_angle_2 = ,
p_angle_3 = ,
p_angle_4 = ,
p_angle_5 = ,
p_angle_6 = ,
p_angle_7 = ,
p_angle_8 = ,
p_angle_9 = ,
p_angle_10 = ,
p_angle_11 = ,
p_angle_12 = ,
p_angle_13 = ,
p_angle_14 = ,
p_angle_15 = ;
parameter p_x_initial = ; //0.6072529351放大了2^16次
parameter p_angle_p90 = 'sd5898240, //90度放大2^16次
p_angle_n90 = -'sd5898240, //-90度
p_angle_p180 = 'sd11796480, //180
p_angle_n180 = -'sd11796480, //-180
p_angle_p0 = 'sd0;
//角度象限判定 角度范围为[-pi,pi]
////象限标识
//00: 第4象限
//01：第1象限
//10：第2象限
//11：第3象限
reg [:] r_angle = 'd0;
reg [:] r_quadrant_flag = 'b00;
reg r_error = 'b0; //角度范围输入错误
always @(posedge i_clk)
begin
if ((i_angle < p_angle_n180) || (i_angle > p_angle_p180)) //越界报错
r_error <= 'b1;
else
r_error <= 'b0;
end
always @(posedge i_clk) //角度象限判定
begin
if ((i_angle >= p_angle_p0) && (i_angle <= p_angle_p90)) //第1象限
begin
r_angle <= i_angle;
r_quadrant_flag <= 'b01;
end
else if (i_angle > p_angle_p90) //第2象限
begin
r_angle <= i_angle - p_angle_p90;
r_quadrant_flag <= 'b10;
end
else if ((i_angle < p_angle_p0) && (i_angle >= p_angle_n90)) //第4象限
begin
r_angle <= i_angle;
r_quadrant_flag <= 'b00;
end
else //第3象限
begin
r_angle <= i_angle - p_angle_n90;
r_quadrant_flag <= 'b11;
end
end //赋初始值
reg [:] r_x_0 = 'd0;
reg [:] r_y_0 = 'd0;
reg [:] r_angle_remain_0 = 'd0;
always @(posedge i_clk)
begin
r_x_0 <= p_x_initial;
r_y_0 <= 'd0;
r_angle_remain_0 <= r_angle;
end
//第1次旋转
reg [:] r_x_1 = 'd0;
reg [:] r_y_1 = 'd0;
reg [:] r_angle_remain_1 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_0[]) //负数
begin
r_x_1 <= r_x_0 + r_y_0;
r_y_1 <= r_y_0 - r_x_0;
r_angle_remain_1 <= r_angle_remain_0 + p_angle_0;
end
else //角度为正
begin
r_x_1 <= r_x_0 - r_y_0;
r_y_1 <= r_y_0 + r_x_0;
r_angle_remain_1 <= r_angle_remain_0 - p_angle_0;
end
end
//第2次旋转
reg [:] r_x_2 = 'd0;
reg [:] r_y_2 = 'd0;
reg [:] r_angle_remain_2 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_1[]) //负数
begin
r_x_2 <= r_x_1 + {{{r_y_1[]}},r_y_1[:]};
r_y_2 <= r_y_1 - {{{r_x_1[]}},r_x_1[:]};
r_angle_remain_2 <= r_angle_remain_1 + p_angle_1;
end
else //角度为正
begin
r_x_2 <= r_x_1 - {{{r_y_1[]}},r_y_1[:]};
r_y_2 <= r_y_1 + {{{r_x_1[]}},r_x_1[:]};
r_angle_remain_2 <= r_angle_remain_1 - p_angle_1;
end
end
//第3次旋转
reg [:] r_x_3 = 'd0;
reg [:] r_y_3 = 'd0;
reg [:] r_angle_remain_3 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_2[]) //负数
begin
r_x_3 <= r_x_2 + {{{r_y_2[]}},r_y_2[:]};
r_y_3 <= r_y_2 - {{{r_x_2[]}},r_x_2[:]};
r_angle_remain_3 <= r_angle_remain_2 + p_angle_2;
end
else //角度为正
begin
r_x_3 <= r_x_2 - {{{r_y_2[]}},r_y_2[:]};
r_y_3 <= r_y_2 + {{{r_x_2[]}},r_x_2[:]};
r_angle_remain_3 <= r_angle_remain_2 - p_angle_2;
end
end
//第4次旋转
reg [:] r_x_4 = 'd0;
reg [:] r_y_4 = 'd0;
reg [:] r_angle_remain_4 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_3[]) //负数
begin
r_x_4 <= r_x_3 + {{{r_y_3[]}},r_y_3[:]};
r_y_4 <= r_y_3 - {{{r_x_3[]}},r_x_3[:]};
r_angle_remain_4 <= r_angle_remain_3 + p_angle_3;
end
else //角度为正
begin
r_x_4 <= r_x_3 - {{{r_y_3[]}},r_y_3[:]};
r_y_4 <= r_y_3 + {{{r_x_3[]}},r_x_3[:]};
r_angle_remain_4 <= r_angle_remain_3 - p_angle_3;
end
end
//第5次旋转
reg [:] r_x_5 = 'd0;
reg [:] r_y_5 = 'd0;
reg [:] r_angle_remain_5 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_4[]) //负数
begin
r_x_5 <= r_x_4 + {{{r_y_4[]}},r_y_4[:]};
r_y_5 <= r_y_4 - {{{r_x_4[]}},r_x_4[:]};
r_angle_remain_5 <= r_angle_remain_4 + p_angle_4;
end
else //角度为正
begin
r_x_5 <= r_x_4 - {{{r_y_4[]}},r_y_4[:]};
r_y_5 <= r_y_4 + {{{r_x_4[]}},r_x_4[:]};
r_angle_remain_5 <= r_angle_remain_4 - p_angle_4;
end
end
//第6次旋转
reg [:] r_x_6 = 'd0;
reg [:] r_y_6 = 'd0;
reg [:] r_angle_remain_6 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_5[]) //负数
begin
r_x_6 <= r_x_5 + {{{r_y_5[]}},r_y_5[:]};
r_y_6 <= r_y_5 - {{{r_x_5[]}},r_x_5[:]};
r_angle_remain_6 <= r_angle_remain_5 + p_angle_5;
end
else //角度为正
begin
r_x_6 <= r_x_5 - {{{r_y_5[]}},r_y_5[:]};
r_y_6 <= r_y_5 + {{{r_x_5[]}},r_x_5[:]};
r_angle_remain_6 <= r_angle_remain_5 - p_angle_5;
end
end
//第7次旋转
reg [:] r_x_7 = 'd0;
reg [:] r_y_7 = 'd0;
reg [:] r_angle_remain_7 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_6[]) //负数
begin
r_x_7 <= r_x_6 + {{{r_y_6[]}},r_y_6[:]};
r_y_7 <= r_y_6 - {{{r_x_6[]}},r_x_6[:]};
r_angle_remain_7 <= r_angle_remain_6 + p_angle_6;
end
else //角度为正
begin
r_x_7 <= r_x_6 - {{{r_y_6[]}},r_y_6[:]};
r_y_7 <= r_y_6 + {{{r_x_6[]}},r_x_6[:]};
r_angle_remain_7 <= r_angle_remain_6 - p_angle_6;
end
end
//第8次旋转
reg [:] r_x_8 = 'd0;
reg [:] r_y_8 = 'd0;
reg [:] r_angle_remain_8 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_7[]) //负数
begin
r_x_8 <= r_x_7 + {{{r_y_7[]}},r_y_7[:]};
r_y_8 <= r_y_7 - {{{r_x_7[]}},r_x_7[:]};
r_angle_remain_8 <= r_angle_remain_7 + p_angle_7;
end
else //角度为正
begin
r_x_8 <= r_x_7 - {{{r_y_7[]}},r_y_7[:]};
r_y_8 <= r_y_7 + {{{r_x_7[]}},r_x_7[:]};
r_angle_remain_8 <= r_angle_remain_7 - p_angle_7;
end
end
//第9次旋转
reg [:] r_x_9 = 'd0;
reg [:] r_y_9 = 'd0;
reg [:] r_angle_remain_9 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_8[]) //负数
begin
r_x_9 <= r_x_8 + {{{r_y_8[]}},r_y_8[:]};
r_y_9 <= r_y_8 - {{{r_x_8[]}},r_x_8[:]};
r_angle_remain_9 <= r_angle_remain_8 + p_angle_8;
end
else //角度为正
begin
r_x_9 <= r_x_8 - {{{r_y_8[]}},r_y_8[:]};
r_y_9 <= r_y_8 + {{{r_x_8[]}},r_x_8[:]};
r_angle_remain_9 <= r_angle_remain_8 - p_angle_8;
end
end
//第10次旋转
reg [:] r_x_10 = 'd0;
reg [:] r_y_10 = 'd0;
reg [:] r_angle_remain_10 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_9[]) //负数
begin
r_x_10 <= r_x_9 + {{{r_y_9[]}},r_y_9[:]};
r_y_10 <= r_y_9 - {{{r_x_9[]}},r_x_9[:]};
r_angle_remain_10 <= r_angle_remain_9 + p_angle_9;
end
else //角度为正
begin
r_x_10 <= r_x_9 - {{{r_y_9[]}},r_y_9[:]};
r_y_10 <= r_y_9 + {{{r_x_9[]}},r_x_9[:]};
r_angle_remain_10 <= r_angle_remain_9 - p_angle_9;
end
end
//第11次旋转
reg [:] r_x_11 = 'd0;
reg [:] r_y_11 = 'd0;
reg [:] r_angle_remain_11 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_10[]) //负数
begin
r_x_11 <= r_x_10 + {{{r_y_10[]}},r_y_10[:]};
r_y_11 <= r_y_10 - {{{r_x_10[]}},r_x_10[:]};
r_angle_remain_11 <= r_angle_remain_10 + p_angle_10;
end
else //角度为正
begin
r_x_11 <= r_x_10 - {{{r_y_10[]}},r_y_10[:]};
r_y_11 <= r_y_10 + {{{r_x_10[]}},r_x_10[:]};
r_angle_remain_11 <= r_angle_remain_10 - p_angle_10;
end
end
//第12次旋转
reg [:] r_x_12 = 'd0;
reg [:] r_y_12 = 'd0;
reg [:] r_angle_remain_12 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_11[]) //负数
begin
r_x_12 <= r_x_11 + {{{r_y_11[]}},r_y_11[:]};
r_y_12 <= r_y_11 - {{{r_x_11[]}},r_x_11[:]};
r_angle_remain_12 <= r_angle_remain_11 + p_angle_11;
end
else //角度为正
begin
r_x_12 <= r_x_11 - {{{r_y_11[]}},r_y_11[:]};
r_y_12 <= r_y_11 + {{{r_x_11[]}},r_x_11[:]};
r_angle_remain_12 <= r_angle_remain_11 - p_angle_11;
end
end
//第13次旋转
reg [:] r_x_13 = 'd0;
reg [:] r_y_13 = 'd0;
reg [:] r_angle_remain_13 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_12[]) //负数
begin
r_x_13 <= r_x_12 + {{{r_y_12[]}},r_y_12[:]};
r_y_13 <= r_y_12 - {{{r_x_12[]}},r_x_12[:]};
r_angle_remain_13 <= r_angle_remain_12 + p_angle_12;
end
else //角度为正
begin
r_x_13 <= r_x_12 - {{{r_y_12[]}},r_y_12[:]};
r_y_13 <= r_y_12 + {{{r_x_12[]}},r_x_12[:]};
r_angle_remain_13 <= r_angle_remain_12 - p_angle_12;
end
end
//第14次旋转
reg [:] r_x_14 = 'd0;
reg [:] r_y_14 = 'd0;
reg [:] r_angle_remain_14 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_13[]) //负数
begin
r_x_14 <= r_x_13 + {{{r_y_13[]}},r_y_13[:]};
r_y_14 <= r_y_13 - {{{r_x_13[]}},r_x_13[:]};
r_angle_remain_14 <= r_angle_remain_13 + p_angle_13;
end
else //角度为正
begin
r_x_14 <= r_x_13 - {{{r_y_13[]}},r_y_13[:]};
r_y_14 <= r_y_13 + {{{r_x_13[]}},r_x_13[:]};
r_angle_remain_14 <= r_angle_remain_13 - p_angle_13;
end
end
//第15次旋转
reg [:] r_x_15 = 'd0;
reg [:] r_y_15 = 'd0;
reg [:] r_angle_remain_15 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_14[]) //负数
begin
r_x_15 <= r_x_14 + {{{r_y_14[]}},r_y_14[:]};
r_y_15 <= r_y_14 - {{{r_x_14[]}},r_x_14[:]};
r_angle_remain_15 <= r_angle_remain_14 + p_angle_14;
end
else //角度为正
begin
r_x_15 <= r_x_14 - {{{r_y_14[]}},r_y_14[:]};
r_y_15 <= r_y_14 + {{{r_x_14[]}},r_x_14[:]};
r_angle_remain_15 <= r_angle_remain_14 - p_angle_14;
end
end
//第16次旋转
reg [:] r_x_16 = 'd0;
reg [:] r_y_16 = 'd0;
reg [:] r_angle_remain_16 = 'd0;
always @(posedge i_clk)
begin
if (r_angle_remain_15[]) //负数
begin
r_x_16 <= r_x_15 + {{{r_y_15[]}},r_y_15[:]};
r_y_16 <= r_y_15 - {{{r_x_15[]}},r_x_15[:]};
r_angle_remain_16 <= r_angle_remain_15 + p_angle_15;
end
else //角度为正
begin
r_x_16 <= r_x_15 - {{{r_y_15[]}},r_y_15[:]};
r_y_16 <= r_y_15 + {{{r_x_15[]}},r_x_15[:]};
r_angle_remain_16 <= r_angle_remain_15 - p_angle_15;
end
end
//计算结果转化为真实结果
//flag延迟16+1+1
reg [:] r_cos_x;
reg [:] r_sin_y;
reg [:] r_quadrant_flag_delay_0 = 'd0;
reg [:] r_quadrant_flag_delay_1 = 'd0;
always @(posedge i_clk)
begin
r_quadrant_flag_delay_0 <= {r_quadrant_flag_delay_0[:],r_quadrant_flag[]};
r_quadrant_flag_delay_1 <= {r_quadrant_flag_delay_1[:],r_quadrant_flag[]};
end
wire [:] demo;
assign demo = {r_quadrant_flag_delay_1[],r_quadrant_flag_delay_0[]};
always @(posedge i_clk)
begin
case ({r_quadrant_flag_delay_1[],r_quadrant_flag_delay_0[]})
'b01: //第1象限
begin
r_cos_x <= r_x_16;
r_sin_y <= r_y_16;
end
'b10: //第2象限
begin
r_cos_x <= ~r_y_16 + 'b1;
r_sin_y <= r_x_16;
end
'b11: //第3象限
begin
r_cos_x <= r_y_16;
r_sin_y <= ~r_x_16 + 'b1;
end
'b00: //第4象限
begin
r_cos_x <= r_x_16;
r_sin_y <= r_y_16;
end
endcase
end ////使能延迟对齐输出,延迟1+1+16+1
reg [:] r_en_delay = 'd0;
always @(posedge i_clk)
begin
r_en_delay <= {r_en_delay[:],i_en};
end
reg [:] r_error_delay = 'd0;
always @(posedge i_clk)
begin
r_error_delay <= {r_error_delay[:],r_error};
end
//信号输出
assign o_cos_x = r_cos_x;
assign o_sin_y = r_sin_y;
assign o_error = r_error_delay[];
assign o_en = r_en_delay[]; endmodule // end the cos_sin_cordic model;
直角坐标转极坐标
已知(x,y)求解(z,r)，
算法流程：
设置迭代次数为16，则x0 = x，y0 = y，z0 = 0，di与yi的符号相反。表示，经过n次旋转，使Pn靠近x轴。
因此，当迭代结束之后，Pn将近似接近x轴，此时yn = 0，可知旋转了θ，即zn = θ = arctan(y/x)。r= xn * ∏cosθi。即r=xn*K。而16次迭代下的K值为0.6072529351。
迭代公式如下：
xi+1 = xi – d iy i2-i
yi+1 = yi + d ix i2-i
zi+1 = zi - diθi
仿真结果如下所示。
x和y均为10000。
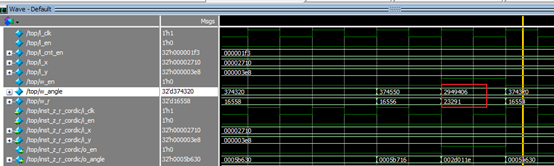
θ = 2949406/2^16 = 45.0044；R = 23291*K=23291* 0.6072529351= 14143.5281114141，跟matlab结果比较：14142.135623731
误差较小。
代码如下，勿做商业用途。
`timescale 1ns/1ps
module z_r_cordic (
input i_clk ,
input i_en ,
input [:] i_x ,
input [:] i_y ,
output o_en ,
output [:] o_angle ,
output [:] o_r
);
////parameter
parameter p_angle_0 = , //45°放大2^16
p_angle_1 = ,
p_angle_2 = ,
p_angle_3 = ,
p_angle_4 = ,
p_angle_5 = ,
p_angle_6 = ,
p_angle_7 = ,
p_angle_8 = ,
p_angle_9 = ,
p_angle_10 = ,
p_angle_11 = ,
p_angle_12 = ,
p_angle_13 = ,
p_angle_14 = ,
p_angle_15 = ; //赋初始值
reg [:] r_x_0 = 'd0;
reg [:] r_y_0 = 'd0;
reg [:] r_angle_remain_0 = 'd0;
always @(posedge i_clk)
begin
r_x_0 <= i_x;
r_y_0 <= i_y;
r_angle_remain_0 <= 'd0;
end
//第1次旋转
reg [:] r_x_1 = 'd0;
reg [:] r_y_1 = 'd0;
reg [:] r_angle_remain_1 = 'd0;
always @(posedge i_clk)
begin
if (r_y_0[]) //负数
begin
r_x_1 <= r_x_0 - r_y_0;
r_y_1 <= r_y_0 + r_x_0;
r_angle_remain_1 <= r_angle_remain_0 - p_angle_0;
end
else //角度为正
begin
r_x_1 <= r_x_0 + r_y_0;
r_y_1 <= r_y_0 - r_x_0;
r_angle_remain_1 <= r_angle_remain_0 + p_angle_0;
end
end
//第2次旋转
reg [:] r_x_2 = 'd0;
reg [:] r_y_2 = 'd0;
reg [:] r_angle_remain_2 = 'd0;
always @(posedge i_clk)
begin
if (r_y_1[]) //负数
begin
r_x_2 <= r_x_1 - {{{r_y_1[]}},r_y_1[:]};
r_y_2 <= r_y_1 + {{{r_x_1[]}},r_x_1[:]};
r_angle_remain_2 <= r_angle_remain_1 - p_angle_1;
end
else //角度为正
begin
r_x_2 <= r_x_1 + {{{r_y_1[]}},r_y_1[:]};
r_y_2 <= r_y_1 - {{{r_x_1[]}},r_x_1[:]};
r_angle_remain_2 <= r_angle_remain_1 + p_angle_1;
end
end
//第3次旋转
reg [:] r_x_3 = 'd0;
reg [:] r_y_3 = 'd0;
reg [:] r_angle_remain_3 = 'd0;
always @(posedge i_clk)
begin
if (r_y_2[]) //负数
begin
r_x_3 <= r_x_2 - {{{r_y_2[]}},r_y_2[:]};
r_y_3 <= r_y_2 + {{{r_x_2[]}},r_x_2[:]};
r_angle_remain_3 <= r_angle_remain_2 - p_angle_2;
end
else //角度为正
begin
r_x_3 <= r_x_2 + {{{r_y_2[]}},r_y_2[:]};
r_y_3 <= r_y_2 - {{{r_x_2[]}},r_x_2[:]};
r_angle_remain_3 <= r_angle_remain_2 + p_angle_2;
end
end
//第4次旋转
reg [:] r_x_4 = 'd0;
reg [:] r_y_4 = 'd0;
reg [:] r_angle_remain_4 = 'd0;
always @(posedge i_clk)
begin
if (r_y_3[]) //负数
begin
r_x_4 <= r_x_3 - {{{r_y_3[]}},r_y_3[:]};
r_y_4 <= r_y_3 + {{{r_x_3[]}},r_x_3[:]};
r_angle_remain_4 <= r_angle_remain_3 - p_angle_3;
end
else //角度为正
begin
r_x_4 <= r_x_3 + {{{r_y_3[]}},r_y_3[:]};
r_y_4 <= r_y_3 - {{{r_x_3[]}},r_x_3[:]};
r_angle_remain_4 <= r_angle_remain_3 + p_angle_3;
end
end
//第5次旋转
reg [:] r_x_5 = 'd0;
reg [:] r_y_5 = 'd0;
reg [:] r_angle_remain_5 = 'd0;
always @(posedge i_clk)
begin
if (r_y_4[]) //负数
begin
r_x_5 <= r_x_4 - {{{r_y_4[]}},r_y_4[:]};
r_y_5 <= r_y_4 + {{{r_x_4[]}},r_x_4[:]};
r_angle_remain_5 <= r_angle_remain_4 - p_angle_4;
end
else //角度为正
begin
r_x_5 <= r_x_4 + {{{r_y_4[]}},r_y_4[:]};
r_y_5 <= r_y_4 - {{{r_x_4[]}},r_x_4[:]};
r_angle_remain_5 <= r_angle_remain_4 + p_angle_4;
end
end
//第6次旋转
reg [:] r_x_6 = 'd0;
reg [:] r_y_6 = 'd0;
reg [:] r_angle_remain_6 = 'd0;
always @(posedge i_clk)
begin
if (r_y_5[]) //负数
begin
r_x_6 <= r_x_5 - {{{r_y_5[]}},r_y_5[:]};
r_y_6 <= r_y_5 + {{{r_x_5[]}},r_x_5[:]};
r_angle_remain_6 <= r_angle_remain_5 - p_angle_5;
end
else //角度为正
begin
r_x_6 <= r_x_5 + {{{r_y_5[]}},r_y_5[:]};
r_y_6 <= r_y_5 - {{{r_x_5[]}},r_x_5[:]};
r_angle_remain_6 <= r_angle_remain_5 + p_angle_5;
end
end
//第7次旋转
reg [:] r_x_7 = 'd0;
reg [:] r_y_7 = 'd0;
reg [:] r_angle_remain_7 = 'd0;
always @(posedge i_clk)
begin
if (r_y_6[]) //负数
begin
r_x_7 <= r_x_6 - {{{r_y_6[]}},r_y_6[:]};
r_y_7 <= r_y_6 + {{{r_x_6[]}},r_x_6[:]};
r_angle_remain_7 <= r_angle_remain_6 - p_angle_6;
end
else //角度为正
begin
r_x_7 <= r_x_6 + {{{r_y_6[]}},r_y_6[:]};
r_y_7 <= r_y_6 - {{{r_x_6[]}},r_x_6[:]};
r_angle_remain_7 <= r_angle_remain_6 + p_angle_6;
end
end
//第8次旋转
reg [:] r_x_8 = 'd0;
reg [:] r_y_8 = 'd0;
reg [:] r_angle_remain_8 = 'd0;
always @(posedge i_clk)
begin
if (r_y_7[]) //负数
begin
r_x_8 <= r_x_7 - {{{r_y_7[]}},r_y_7[:]};
r_y_8 <= r_y_7 + {{{r_x_7[]}},r_x_7[:]};
r_angle_remain_8 <= r_angle_remain_7 - p_angle_7;
end
else //角度为正
begin
r_x_8 <= r_x_7 + {{{r_y_7[]}},r_y_7[:]};
r_y_8 <= r_y_7 - {{{r_x_7[]}},r_x_7[:]};
r_angle_remain_8 <= r_angle_remain_7 + p_angle_7;
end
end
//第9次旋转
reg [:] r_x_9 = 'd0;
reg [:] r_y_9 = 'd0;
reg [:] r_angle_remain_9 = 'd0;
always @(posedge i_clk)
begin
if (r_y_8[]) //负数
begin
r_x_9 <= r_x_8 - {{{r_y_8[]}},r_y_8[:]};
r_y_9 <= r_y_8 + {{{r_x_8[]}},r_x_8[:]};
r_angle_remain_9 <= r_angle_remain_8 - p_angle_8;
end
else //角度为正
begin
r_x_9 <= r_x_8 + {{{r_y_8[]}},r_y_8[:]};
r_y_9 <= r_y_8 - {{{r_x_8[]}},r_x_8[:]};
r_angle_remain_9 <= r_angle_remain_8 + p_angle_8;
end
end
//第10次旋转
reg [:] r_x_10 = 'd0;
reg [:] r_y_10 = 'd0;
reg [:] r_angle_remain_10 = 'd0;
always @(posedge i_clk)
begin
if (r_y_9[]) //负数
begin
r_x_10 <= r_x_9 - {{{r_y_9[]}},r_y_9[:]};
r_y_10 <= r_y_9 + {{{r_x_9[]}},r_x_9[:]};
r_angle_remain_10 <= r_angle_remain_9 - p_angle_9;
end
else //角度为正
begin
r_x_10 <= r_x_9 + {{{r_y_9[]}},r_y_9[:]};
r_y_10 <= r_y_9 - {{{r_x_9[]}},r_x_9[:]};
r_angle_remain_10 <= r_angle_remain_9 + p_angle_9;
end
end
//第11次旋转
reg [:] r_x_11 = 'd0;
reg [:] r_y_11 = 'd0;
reg [:] r_angle_remain_11 = 'd0;
always @(posedge i_clk)
begin
if (r_y_10[]) //负数
begin
r_x_11 <= r_x_10 - {{{r_y_10[]}},r_y_10[:]};
r_y_11 <= r_y_10 + {{{r_x_10[]}},r_x_10[:]};
r_angle_remain_11 <= r_angle_remain_10 - p_angle_10;
end
else //角度为正
begin
r_x_11 <= r_x_10 + {{{r_y_10[]}},r_y_10[:]};
r_y_11 <= r_y_10 - {{{r_x_10[]}},r_x_10[:]};
r_angle_remain_11 <= r_angle_remain_10 + p_angle_10;
end
end
//第12次旋转
reg [:] r_x_12 = 'd0;
reg [:] r_y_12 = 'd0;
reg [:] r_angle_remain_12 = 'd0;
always @(posedge i_clk)
begin
if (r_y_11[]) //负数
begin
r_x_12 <= r_x_11 - {{{r_y_11[]}},r_y_11[:]};
r_y_12 <= r_y_11 + {{{r_x_11[]}},r_x_11[:]};
r_angle_remain_12 <= r_angle_remain_11 - p_angle_11;
end
else //角度为正
begin
r_x_12 <= r_x_11 + {{{r_y_11[]}},r_y_11[:]};
r_y_12 <= r_y_11 - {{{r_x_11[]}},r_x_11[:]};
r_angle_remain_12 <= r_angle_remain_11 + p_angle_11;
end
end
//第13次旋转
reg [:] r_x_13 = 'd0;
reg [:] r_y_13 = 'd0;
reg [:] r_angle_remain_13 = 'd0;
always @(posedge i_clk)
begin
if (r_y_12[]) //负数
begin
r_x_13 <= r_x_12 - {{{r_y_12[]}},r_y_12[:]};
r_y_13 <= r_y_12 + {{{r_x_12[]}},r_x_12[:]};
r_angle_remain_13 <= r_angle_remain_12 - p_angle_12;
end
else //角度为正
begin
r_x_13 <= r_x_12 + {{{r_y_12[]}},r_y_12[:]};
r_y_13 <= r_y_12 - {{{r_x_12[]}},r_x_12[:]};
r_angle_remain_13 <= r_angle_remain_12 + p_angle_12;
end
end
//第14次旋转
reg [:] r_x_14 = 'd0;
reg [:] r_y_14 = 'd0;
reg [:] r_angle_remain_14 = 'd0;
always @(posedge i_clk)
begin
if (r_y_13[]) //负数
begin
r_x_14 <= r_x_13 - {{{r_y_13[]}},r_y_13[:]};
r_y_14 <= r_y_13 + {{{r_x_13[]}},r_x_13[:]};
r_angle_remain_14 <= r_angle_remain_13 - p_angle_13;
end
else //角度为正
begin
r_x_14 <= r_x_13 + {{{r_y_13[]}},r_y_13[:]};
r_y_14 <= r_y_13 - {{{r_x_13[]}},r_x_13[:]};
r_angle_remain_14 <= r_angle_remain_13 + p_angle_13;
end
end
//第15次旋转
reg [:] r_x_15 = 'd0;
reg [:] r_y_15 = 'd0;
reg [:] r_angle_remain_15 = 'd0;
always @(posedge i_clk)
begin
if (r_y_14[]) //负数
begin
r_x_15 <= r_x_14 - {{{r_y_14[]}},r_y_14[:]};
r_y_15 <= r_y_14 + {{{r_x_14[]}},r_x_14[:]};
r_angle_remain_15 <= r_angle_remain_14 - p_angle_14;
end
else //角度为正
begin
r_x_15 <= r_x_14 + {{{r_y_14[]}},r_y_14[:]};
r_y_15 <= r_y_14 - {{{r_x_14[]}},r_x_14[:]};
r_angle_remain_15 <= r_angle_remain_14 + p_angle_14;
end
end
//第16次旋转
reg [:] r_x_16 = 'd0;
reg [:] r_y_16 = 'd0;
reg [:] r_angle_remain_16 = 'd0;
always @(posedge i_clk)
begin
if (r_y_14[]) //负数
begin
r_x_16 <= r_x_15 - {{{r_y_15[]}},r_y_15[:]};
r_y_16 <= r_y_15 + {{{r_x_15[]}},r_x_15[:]};
r_angle_remain_16 <= r_angle_remain_15 - p_angle_15;
end
else //角度为正
begin
r_x_16 <= r_x_15 + {{{r_y_15[]}},r_y_15[:]};
r_y_16 <= r_y_15 - {{{r_x_15[]}},r_x_15[:]};
r_angle_remain_16 <= r_angle_remain_15 + p_angle_15;
end
end
////使能延迟对齐输出
reg [:] r_en_delay = 'd0;
always @(posedge i_clk)
begin
r_en_delay <= {r_en_delay[:],i_en};
end
////信号输出
assign o_angle = r_angle_remain_16;
assign o_r = r_x_16;
assign o_en = r_en_delay[]; endmodule // end the z_r_cordic model;
双曲反正切的妙用
双曲反正切有啥用呢，如果你想求log10，冥思苦想，这玩意咋用verilog求？而我们知道如下公式：
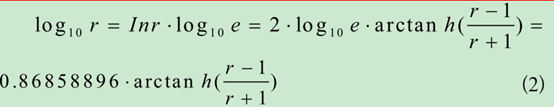
则log10就可以转化为求解arctanh的值。而我们知道，arctanh是可以用cordic在双曲模式下求解其值的。所以，log就可以用cordic求解。
在双曲模式下的算法迭代跟其他的不一样，涉及到收敛问题，且从N为4开始，每当3k+1的项需要重复迭代。即1,2,3,4,4,5,6.....12,13,13,14.....
而同时简单的正数迭代，y和x的取值范围十分有限，对于arctanh((r-1)/(r+1))的r最大值仅仅为9，简直是不可用的。
还好前人早已想到了这个问题，请参考论文，需要添加负数次的迭代，扩大定义域。
算法过程：
1.取x=r+1,y=r-1,z=0。当Y迭代逼近0的时候，z的值即为arctanh((r-1)/(r+1))的值。取迭代次数为16次的时候，N=-5起始迭代。则可以事先求解出相应的arctanh值作为常量供迭代方程加减。
2.迭代公式，选取从N=-5处开始迭代，则有
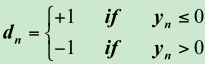
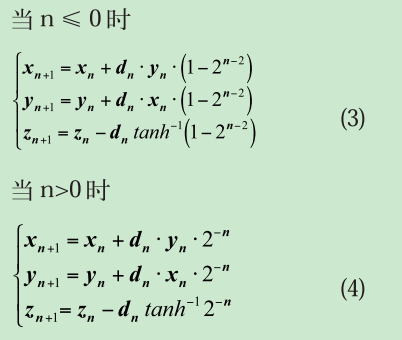
3.编写verilog代码。
仿真一下看看。
r=10仿真结果如下所示：x,y首先均左移8位。
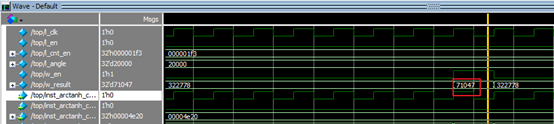
log10(10) = 71047/2^16*0.86858896 = 0.9416
log10(100) = 125429/2^16*0.86858896 = 1.6624
log10(1000) =225544/2^16*0.86858896 = 2.9893
log10(10000) = 299021/2^16*0.86858896 = 3.9631
有一定的误差，跟迭代次数和迭代输入值x,y有关
注意事项：（1）处理中间结果的越界问题，位宽需要注意。
（2）如果r输入是个很小的数，比如10，可能还没迭代两次，y就到0了，必然导致结果的误差过大，则可以放大x和y，毕竟我们知道arctanh(y/x)=arctanh(y*k/(x*k))的。
所以结果并不会发生改变，但可以使得迭代更多次，保证精度。当然预先做个数值范围判定移位更佳。
（3）算术移位的问题，必须定义signed，否则会有问题的。还是老实使用拼接截位操作得好。
以上只是对算法进行了功能的实现，侧重点并不在资源量的最优。
以上。
使用帅气的cordic算法进行坐标系互转及log10的求解的更多相关文章
- 基于FPGA的Cordic算法实现
CORDIC(Coordinate Rotation Digital Computer)算法即坐标旋转数字计算方法,是J.D.Volder1于1959年首次提出,主要用于三角函数.双曲线.指数.对数的 ...
- 三角函数计算，Cordic 算法入门
[-] 三角函数计算Cordic 算法入门 从二分查找法说起 减少乘法运算 消除乘法运算 三角函数计算,Cordic 算法入门 三角函数的计算是个复杂的主题,有计算机之前,人们通常通过查找三角函数表来 ...
- （转）三角函数计算，Cordic 算法入门
由于最近要使用atan2函数,但是时间上消耗比较多,因而网上搜了一下简化的算法. 原帖地址:http://blog.csdn.net/liyuanbhu/article/details/8458769 ...
- 基于FPGA的cordic算法的verilog初步实现
最近在看cordic算法,由于还不会使用matlab,真是痛苦,一系列的笔算才大概明白了这个算法是怎么回事.于是尝试用verilog来实现.用verilog实现之前先参考软件的程序,于是先看了此博文h ...
- Cordic 算法之 反正切
在通信的算法中,常采用Cordic算法之一,知道角度产生正交的的正弦余弦, 或者知道正弦和余弦求角度,求反正切. 1. 求正弦和余弦值. 方法:旋转角度,得到正弦余弦值: 再旋转角度,到达下一个正弦余 ...
- Cordic 算法的原理介绍
cordic 算法知道正弦和余弦值,求反正切,即角度. 采用用不断的旋转求出对应的正弦余弦值,是一种近似求解发. 旋转的角度很讲求,每次旋转的角度必须使得 正切值近似等于 1/(2^N).旋转的目的是 ...
- Cordic算法——verilog实现
上两篇博文Cordic算法--圆周系统之旋转模式.Cordic算法--圆周系统之向量模式做了理论分析和实现,但是所用到的变量依然是浮点型,而cordic真正的用处是基于FPGA等只能处理定点的平台.只 ...
- Cordic算法——圆周系统之向量模式
旋转模式用来解决三角函数,实现极坐标到直角坐标的转换,基础理论请参考Cordic算法--圆周系统之旋转模式.那么,向量模式则用来解决反三角函数的问题,体现的应用主要是直角坐标向极坐标转换,即已知一点的 ...
- Cordic算法——圆周系统之旋转模式
三角函数的计算是个复杂的主题,有计算机之前,人们通常通过查找三角函数表来计算任意角度的三角函数的值.这种表格在人们刚刚产生三角函数的概念的时候就已经有了,它们通常是通过从已知值(比如sin(π/2)= ...
随机推荐
- mysql占用服务器cpu过高的原因以及解决办法
登陆Mysql: mysql -p<port> -u<user> -p<pwd> mysql> show processlist; show processl ...
- 阶段5 3.微服务项目【学成在线】_day17 用户认证 Zuul_08-用户认证-认证服务查询数据库-用户登录前端
点击登陆注册链接 跳转到登陆的页面 门户的前端代码 当前路径base64编码 登陆的表单,在学习中心的前端. 这就是登陆的表单 这是表单的校验 请求服务端的接口 登陆请求的方法 请求的地址nginx上 ...
- Mysql常见索引介绍
索引是一种特殊的文件,包含了对数据表中所有记录的引用指针.InnoDB引擎的数据库,其上的索引是表空间的一个组成部分. (1).索引的优缺点 优点:加快搜索速度,减少查询时间 缺点:索引是以文件的形式 ...
- LeetCode_160. Intersection of Two Linked Lists
160. Intersection of Two Linked Lists Easy Write a program to find the node at which the intersectio ...
- mysql导入、导出 ( 带视图）
1创建账号授权 grant all privileges on jenkinsddbes.* to 'jenkinsddbes'@'%' identified by '1iN@Da12tA&* ...
- SLAM十四讲中Sophus库安装
Sophus截止目前有很多版本,其中大体分为两类,一种是用模板实现的方法,一种是用非模板类实现的,SLAM十四讲中使用的是非模板类库,clone Sophus: git clone http://gi ...
- Android Monkey压力测试（转）
参考链接:https://www.cnblogs.com/yyh8/p/6707745.html Monkey 是Android SDK提供的一个命令行工具, 可以简单,方便地运行在任何版本的Andr ...
- C#基础知识学习 linq 和拉姆表达式二
- 【转】Entity Framework简介
Entity Framework Core 可基于现有数据库创建模型,也可基于模型创建数据库. 以下文字来源于:http://www.entityframeworktutorial.net/what- ...
- Java面试 - == 和 equals 的区别?
==:如果比较的对象是基本数据类型,则比较的是数值是否一致:如果比较的是引用数据类型,则比较的是对象的地址值是否一致. equals():equals()方法不能用于比较基本数据类型的对象,如果对象和 ...