什么是B+树

什么是B+树呢？在说B+树之前我们先了解一下为什么要有B树，其实这些树最开始都是为了解决某种系统中，查询效率低的问题。B树其实最开始源于的是二叉树，二叉树是只有左右孩子的树，当数据量越大的时候，二叉树的节点越多，那么当从根节点搜索的时候，影响查询效率。所以如果这些节点存储在外存储器中的话，每访问一个节点，相当于进行了一次I/O操作。

这里面说下外存储器和内存储器：

外存储器：就是将数据存储到磁盘中，每次查找的某个元素的时候都要取磁盘中查找，然后再写入内存中，容量大，但是查询效率低。

内存储器：就是将数据放在内存中，查询快，但是容量小。

我们大致了解了B树和什么是外存储器，内存储器，那么就知道其实B+树就是为了解决数据量大的时候存储在外存储器时候，查找效率低的问题。接下来就说下B+树的特点：

1. 中间元素不存数据，只是当索引用，所有数据都保存在叶子结点中。
2. 所有的中间节点在子节点中要么是最大的元素要么是最小的元素 。
3. 叶子结点包含所有的数据，和指向这些元素的指针，而且叶子结点的元素形成了自小向大这样子的链表。

如下这个图就很好的说明了B+的特点

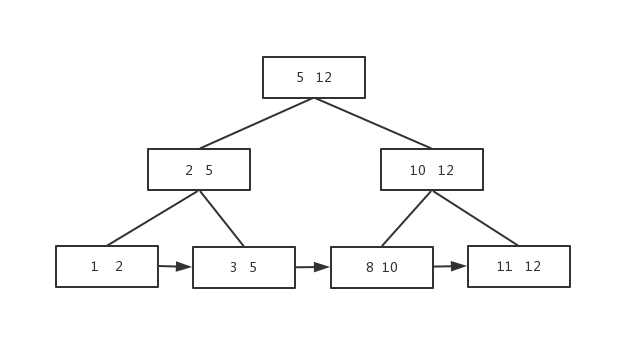
看图其实可以看到一个节点可以存放多个数据，查找一个节点的时候可以有多个元素，大大提升查找效率，这就是为什么数据库索引用的就是B+树，因为索引很大，不可能都放在内存中，所以通常是以索引文件的形式放在磁盘上，所以当查找数据的时候就会有磁盘I/O的消耗，而B+树正可以解决这种问题，减少与磁盘的交互，因为进行一次I/O操作可以得到很多数据，增大查找数据的命中率。

这就可以很明显的看出B+树的优势：

1. 单个节点可以存储更多的数据，减少I/O的次数。
2. 查找性能更稳定，因为都是要查找到叶子结点。
3. 叶子结点形成了有序链表，便于查询。

B+树是怎么进行查找的呢，分为单元素查找和范围查找

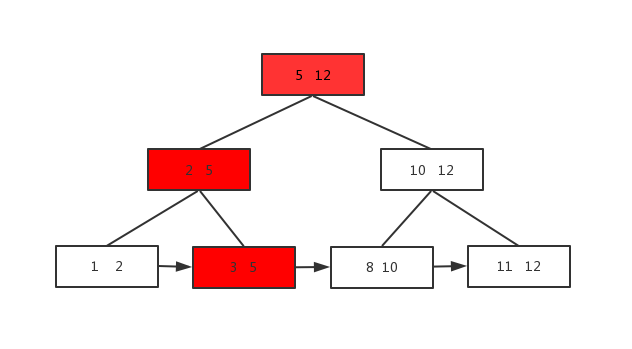
单元素查找是从根一直查找到叶子结点，即使中间结点有这个元素也要查到叶子结点，因为中间结点只是索引，不存数据。比如要查元素3，如图：

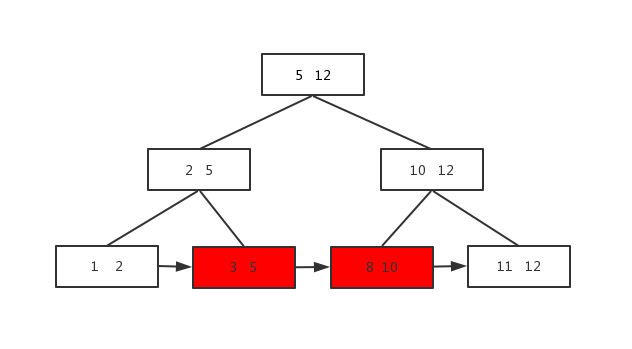
范围查找是直接从链表查，比如要查元素3到元素8的，如图：

也是参考了其他人的博客，自己也总结了一下，有说的不对的地方希望大家能够多多指出，以后也会继续努力哒，嘻嘻～