Python——EM(期望极大算法)教学(附详细代码与注解)

　　今天，我们详细的讲一下EM算法。

　　前提准备

　　Jupyter notebook 或 Pycharm

　　火狐浏览器或谷歌浏览器

　　win7或win10电脑一台

　　网盘提取csv数据

　　需求分析

　　实现高斯混合模型的 EM 算法(GMM_EM)

　　高斯混合模型是多个高斯模型的线性叠加而成的，高斯混合模型的概率分布表示如下：

　　

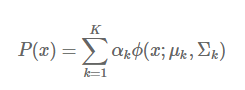
　　其中，k表示模型的个数，αkα_kαk​ 是第 k 个模型的系数，表示出现该模型的概率，ϕ(x;μk,Σk) 是第 k 个高斯模型的概率分布。

　　E步：样本 xix_ixi​来自于第 k 个模型的概率，我们把这个概率称为模型 k 对样本 xix_ixi​ 的“责任”，也叫“响应度”，记作 γ(ik)γ_(ik)γ(​ik)，计算公式如下：

　　

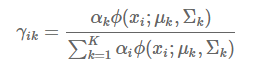
　　M步：根据样本和当前 γ 矩阵重新估计参数，注意这里 x 为列向量，计算公式如下：

　　【目标】给定一堆没有标签的样本和模型个数 K，以此求得混合模型的参数，然后就可以用这个模型来对样本进行聚类。

　　python代码如下：

　　import numpy as np

　　import matplotlib.pyplot as plt

　　from scipy.stats import multivariate_normal #本问题考虑的是高斯混合模型，所以导入多元高斯分布multivariate_normal

　　def prob_Y_k(Y,mu_k,cov_k): #Y为样本矩阵

　　norm = multivariate_normal(mean = mu_k , cov = cov_k) #生成多元正太分布，mu为第k个模型的均值，cov为第k个模型的协方差矩阵(协方差矩阵必须是实对称矩阵)

　　return norm.pdf(Y) #返回样本Y来自于第k个模型的概率

　　def Estep(Y,mu,cov,alpha): #Y为样本矩阵，alpha为权重

　　N = Y.shape[0] #样本数

　　K = alpha.shape[0] #模型数

　　assert N>1 , "There must be more than one sample!" #为避免单个样本导致返回的结果的类型不一致，因此要求样本数必须大于一

　　assert K>1 , "There must be more than one gaussian model!" #为避免单个模型结果的类型不一致，因此要求模型须大于一

　　gamma = np.mat(np.zeros((N,K))) #初始化响应度矩阵，行对应样本数，列对应模型数

　　prob = np.zeros((N,K)) #初始化所有样本出现的概率矩阵，行对应样本数，列对应响应度

　　for k in range(K):

　　prob[:,k] = prob_Y_k(Y,mu[k],cov[k]) #第k个模型的概率prob_Y_k

　　prob = np.mat(prob) #K个prob放入数组中

　　for k in range(K):

　　gamma[:,k] = alpha[k] * prob[:,k] #计算模型k对样本i的响应度

　　for i in range(N):

　　gamma[i,:] /= np.sum(gamma[i,:]) #第i个样本的占总样本的响应程度

　　return gamma #gamma为响应度矩阵

　　def Mstep(Y,gamma): #传入样本矩阵Y和Estep得到的gamma响应度矩阵

　　N, D = Y.shape #N为样本数，D为特征数

　　K = gamma.shape[1] #模型数

　　mu = np.zeros((K,D)) #初始化参数均值mu，每个模型的D维各有均值故mu的矩阵为K行D列

　　cov = [] #初始化参数协方差矩阵

　　alpha = np.zeros(K) # 初始化权重数组，每个模型都有权值

　　#接下来是更新每个模型的参数

　　for k in range(K):

　　Nk = np.sum(gamma[:,k]) #第k个模型所有样本的响应度之和

　　mu[k,:] = np.sum(np.multiply(Y, gamma[:,k]),axis=0)/Nk #更新参数均值mu，对每个特征求均值

　　cov_k = (Y - mu[k]).T * np.multiply((Y - mu[k]), gamma[:,k]) / Nk #更新cov

　　cov = np.append(cov_k)

　　alpha[k] = Nk / N

　　cov = np.array(cov)

　　return mu, cov, alpha

　　def normalize_data(Y): #将所有数据进行归一化处理，

　　for i in range(Y.shape[1]):

　　max_data = Y[:,i].max()

　　min_data = Y[:,i].min()

　　Y[:,i] = (Y[:,i] - min_data)/(max_data - min_data) #此处用到min-max归一化

　　debug("Data Normalized")

　　return Y

　　def init_params(shape,K): #在执行该算法之前，需要先给出一个初始化的模型参数。我们让每个模型的μ为随机值,Σ 为单位矩阵，α 为 1/K，即每个模型初始时都是等概率出现的。

　　N, D = shape郑州人流手术多少钱 http://mobile.chnk120.com/

　　mu = np.random.rand(K, D) #生成一个K行D列的[0,1)之间的数组

　　cov = np.array([np.eye(D)] * K) #生成K个D维的对角矩阵

　　alpha = np.array([1.0 / K] * K) #生成K个权重

　　debug("Parameters initialized.")

　　debug("mu:",mu, "cov:",cov ,"alpha:",alpha,sep = "\n" )

　　return mu, cov, alpha

　　def GMM_EM(Y, K, times): #高斯混合EM算法,Y为给定样本矩阵，K为模型个数，times为迭代次数，目的是求该模型的参数

　　Y = normalize_data(Y) #调用前面定义的normalize_data函数，归一化样本矩阵Y

　　mu, cov, alpha = init_params(Y.shape, K) #调用init_params函数得到初始化的参数mu,cov,alpha

　　for i in range(times):

　　gamma = Estep(Y, mu, cov, alpha) #调用Estep得到响应度矩阵

　　mu, cov, alpha = Mstep(Y, gamma) #调用Mstep得到更新后的参数mu,cov,alpha

　　debug("{sep} Result {sep}".format(sep="-"*20))

　　debug("mu:", mu , "cov:",cov , "alpha:",alpha , sep="\n")

　　return mu,cov,alpha

　　import matplotlib.pyplot as plt

　　from gmm import *

　　DEBUG = True

　　Y = np.loadtxt("gmm.data") #载入数据

　　matY = np.matrix(Y ,copy = True)

　　K = 2 #模型个数(相当于聚类的类别个数)

　　mu, cov, alpha = GMM_EM(matY , K , 100) #调用GMM_EM函数，计算GMM模型参数

　　N = Y.shape[0]

　　gamma = Estep(matY, mu, cov, alpha) #求当前模型参数下，各模型对样本的响应矩阵

　　category = gamma.argmax(axis = 1).flatten().tolist()[0] #对每个样本，求响应度最大的模型下标，作为其类别标识

　　class1 = np.array([Y[i] for i in range(N) if category[i] == 0]) #将每个样本放入对应样本的列表中

　　class2 = np.array([Y[i] for i in range(N) if category[i] == 1])

　　plt.plot(class1[:,0],class1[:,1], 'rs' ,label = "class1")

　　plt.plot(class2[:,0],class2[:,1], 'bo' ,label = "class2")

　　plt.legend(loc = "best")

　　plt.title("GMM Clustering By EM Algorithm")

　　plt.show()

　　import numpy as np

　　import matplotlib.pyplot as plt

　　cov1 = np.mat("0.3 0 ; 0 0.1") #2维协方差矩阵(必须是对角矩阵)

　　cov2 = np.mat("0.2 0 ; 0 0.3")

　　mu1 = np.array([0,1])

　　mu2 = np.array([2,1])

　　sample = np.zeros((100,2)) #初始化100个样本，样本特征为2

　　sample[:30, :] = np.random.multivariate_normal(mean=mu1, cov=cov1, size=30) #生成多元正态分布矩阵

　　sample[30:, :] = np.random.multivariate_normal(mean=mu2, cov=cov2, size=70)

　　np.savetxt("sample.data",sample) # 将array保存到txt文件中

　　plt.plot(sample[:30, 0], sample[:30, 1], "bo") #30个样本用蓝色圆圈标记

　　plt.plot(sample[30:, 0], sample[30:, 1], "rs") #70个样本用红色方块标记

　　plt.title("sample_data")

　　plt.show()