Python回归分析五部曲（一）—简单线性回归

回归最初是遗传学中的一个名词，是由英国生物学家兼统计学家高尔顿首先提出来的，他在研究人类身高的时候发现：高个子回归人类的平均身高，而矮个子则从另一方向回归人类的平均身高；

回归分析整体逻辑

• 回归分析（Regression Analysis）

  • 研究自变量与因变量之间关系形式的分析方法，它主要是通过建立因变量y与影响它的自变量 x_i(i=1,2,3… …)之间的回归模型，来预测因变量y的发展趋向。

• 回归分析的分类

  • 线性回归分析

    • 简单线性回归
    • 多重线性回归

  • 非线性回归分析

    • 逻辑回归
    • 神经网络

• 回归分析的步骤

  • 根据预测目标，确定自变量和因变量

  • 绘制散点图，确定回归模型类型

  • 估计模型参数，建立回归模型

  • 对回归模型进行检验

  • 利用回归模型进行预测

简单线性回归模型

1.基础逻辑

y=a+bx+e

该模型也称作一元一次回归方程，模型中：

• y：因变量
• x：自变量
• a：常数项（回归直线在y轴上的截距）
• b：回归系数（回归直线的斜率）
• e：随机误差（随机因素对因变量所产生的影响）
  
  • e的平方和也称为残差，残差是判断线性回归拟合好坏的重要指标之一

从简单线性回归模型可以知道，简单线性回归是研究一个因变量与一个自变量间线性关系的方法

2.案例实操

下面我们来看一个案例，某金融公司在多次进行活动推广后记录了活动推广费用及金融产品销售额数据，如下表所示

因为活动推广有明显效果，现在的需求是投入60万的推广费，能得到多少的销售额呢？这时我们就可以使用简单线性回归模型去解决这个问题，下面，我们用这个案例来学习，如何进行简单线性回归分析；

（1）第一步 确定变量

• 根据预测目标，确定自变量和因变量

  • 问题：投入60万的推广费，能够带来多少的销售额？

  • 确定因变量和自变量很简单，谁是已知，谁就是自变量，谁是未知，就就是因变量，因此，推广费是自变量，销售额是因变量；

import numpy
from pandas import read_csv
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression

data = read_csv(
    'file:///Users/apple/Desktop/jacky_1.csv',encoding='GBK'
)

（2）第二步 确定类型

• 绘制散点图，确定回归模型类型

  • 根据前面的数据，画出自变量与因变量的散点图，看看是否可以建立回归方程，在简单线性回归分析中，我们只需要确定自变量与因变量的相关度为强相关性，即可确定可以建立简单线性回归方程，根据jacky前面的文章分享《Python相关分析》，我们很容易就求解出推广费与销售额之间的相关系数是0.94，也就是具有强相关性，从散点图中也可以看出，二者是有明显的线性相关的，也就是推广费越大，销售额也就越大

#画出散点图，求x和y的相关系数
plt.scatter(data.活动推广费,data.销售额)

data.corr()

（3）第三步 建立模型

• 估计模型参数，建立回归模型

  要建立回归模型，就要先估计出回归模型的参数A和B，那么如何得到最佳的A和B，使得尽可能多的数据点落在或者更加靠近这条拟合出来的直线上呢？

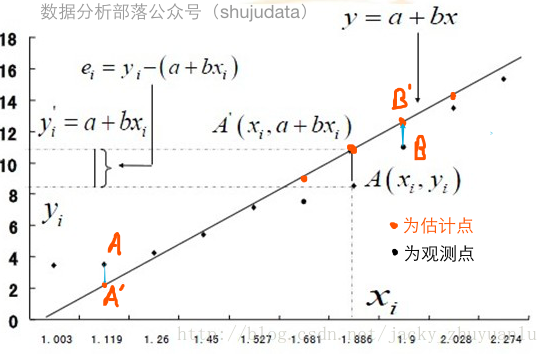
统计学家研究出一个方法，就是最小二乘法，最小二乘法又称最小平方法，通过最小化误差的平方和寻找数据的最佳直线，这个误差就是实际观测点和估计点间的距离；

最小二乘法名字的缘由有二个：一是要将误差最小化，二是使误差最小化的方法是使误差的平方和最小化；在古汉语中，平方称为二乘，用平方的原因就是要规避负数对计算的影响，所以最小二乘法在回归模型上的应用就是要使得实际观测点和估计点的平方和达到最小，也就是上面所说的使得尽可能多的数据点落在或者说更加靠近这条拟合出来的直线上；

我们只要了解最小二乘法的原理即可，具体计算的过程就交给Python处理。


#估计模型参数，建立回归模型
'''
(1) 首先导入简单线性回归的求解类LinearRegression
(2) 然后使用该类进行建模，得到lrModel的模型变量
'''

lrModel = LinearRegression()
#(3) 接着，我们把自变量和因变量选择出来
x = data[['活动推广费']]
y = data[['销售额']]

#模型训练
'''
调用模型的fit方法，对模型进行训练
这个训练过程就是参数求解的过程
并对模型进行拟合
'''
lrModel.fit(x,y)

（4）第四步 模型检验

• 对回归模型进行检验

  • 回归方程的精度就是用来表示实际观测点和回归方程的拟合程度的指标，使用判定系数来度量。

判定系数＝相关系数R2=ESSTSS=1−RSSTSS

其中，数据分析部落公众号(shujudata)

TSS=∑(Yi−Y¯)2总离差平方和

ESS=∑(Yi−Y¯)2回归差平方和

RSS=∑(Yi−Y¯)2残差平方和

解释：判定系数等于相关系数R的平方用于表示拟合得到的模型能解释因变量变化的百分比，R平方越接近于1，表示回归模型拟合效果越好

如果拟合出来的回归模型精度符合我们的要求，那么我们可以使用拟合出来的回归模型，根据已有的自变量数据来预测需要的因变量对应的结果

#对回归模型进行检验
lrModel.score(x,y)

执行代码可以看到，模型的评分为0.887,是非常不错的一个评分，我们就可以使用这个模型进行未知数据的预测了

（5）第五步 模型预测

• 调用模型的predict方法，这个就是使用sklearn进行简单线性回归的求解过程；

lrModel.predict([[60],[70]])

• 如果需要获取到拟合出来的参数各是多少，可以使用模型的intercept属性查看参数a(截距)，使用coef属性查看参数b

#查看截距
alpha = lrModel.intercept_[0]

#查看参数
beta = lrModel.coef_[0][0]

alpha + beta*numpy.array([60,70])

3.完整代码

import numpy
from pandas import read_csv
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression

data = read_csv(
    'file:///Users/apple/Desktop/jacky_1.csv',encoding='GBK'
)

#画出散点图，求x和y的相关系数
plt.scatter(data.活动推广费,data.销售额)

data.corr()

#估计模型参数，建立回归模型
'''
(1) 首先导入简单线性回归的求解类LinearRegression
(2) 然后使用该类进行建模，得到lrModel的模型变量
'''

lrModel = LinearRegression()
#(3) 接着，我们把自变量和因变量选择出来
x = data[['活动推广费']]
y = data[['销售额']]

#模型训练
'''
调用模型的fit方法，对模型进行训练
这个训练过程就是参数求解的过程
并对模型进行拟合
'''
lrModel.fit(x,y)

#对回归模型进行检验
lrModel.score(x,y)

#利用回归模型进行预测
lrModel.predict([[60],[70]])

#查看截距
alpha = lrModel.intercept_[0]

#查看参数
beta = lrModel.coef_[0][0]

alpha + beta*numpy.array([60,70])

4.总结-sklearn建模流程

• sklearn建模流程

  • 建立模型

    • lrModel = sklearn.linear_model.LinearRegression()

  • 训练模型

    • lrModel.fit(x,y)

  • 模型评估

    • lrModel.score(x,y)

  • 模型预测

    • lrModel.predict(x)