缓动公式整理（附：C#实现及WPF原版对比）

前言

缓动在动画效果中应用非常广泛，在合适的时候使用一些缓动效果会使得效果更加符合人的直观感受，简单来说，会显得更加自然。

WPF提供了11种缓动效果，涵盖了大部分的使用场景。不过如果需要在非WPF下使用这些缓动效果，就需要知道对应的曲线公式了。因为公式是通用的，所以可以很轻松的使用其他语言实现。

由于本人数学水平有限，所以本文注重的应用而不是原理。在本文中，将会使用C#去实现，并附上与WPF原版的对比效果。

本文参考：

1，https://docs.microsoft.com/zh-cn/dotnet/desktop/wpf/graphics-multimedia/easing-functions?view=netframeworkdesktop-4.8

2，https://github.com/ai/easings.net

文末会附上示例源代码，需要者可自行下载。

本文地址：https://www.cnblogs.com/lesliexin/p/13594811.html

---

一、WPF中的缓动效果

在WPF中，共有11种：Back，Bounce，Circle，Quadratic，Cubic，Quartic，Quintic，Elastic，Exponential，Sine，Power。不过严格来说只有7种，因为Quadratic，Cubic，Quartic，Quintic是由Power去实现的，由于Power参数未定，所以仅实现前10种效果。

所以对于每个缓动效果而言，都有三种模式：缓入（EaseIn）、缓出（EaseOut）、缓入缓出（EaseInOut）。

---

二、公式与动画

一个元素的动画效果，其实就是这个元素变化的快慢，也就是速度。速度与时间间隔和该时间间隔内运动距离两个变量有关。在实际实现中，时间间隔是相等的，那么速度的变化与距离的变化就成正比。在一个二维坐标当中，横坐标为时间，纵坐标为距离，那么其形成的曲线中，曲线越陡，速度越快，曲线越平缓，则速度越慢。

而我们使用公式的目的，就是取得这个纵坐标的值。

不过，要注意的是，我们获取的曲线的时间范围是：0~1，这不是具体的1秒或1毫秒，而是“单位1”。举例来说，如果一个动画效果时长是2000ms，那么在第x ms时，对应的单位时间就是x/2000。

---

三、缓动公式、缓动效果、与WPF对比

1，Back

曲线（图源自MSDN）：

1.1，曲线公式

public static double Back(double x, LEaseMode easeMode)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return 2.70158 * x * x * x - 1.70158 * x * x;
        case LEaseMode.EaseOut:
            return 1 + 2.70158 * Math.Pow(x - 1, 3) + 1.70158 * Math.Pow(x - 1, 2);
        case LEaseMode.EaseInOut:
            return x < 0.5 ? (Math.Pow(2 * x, 2) * (7.189819 * x - 2.5949095)) / 2 : (Math.Pow(2 * x - 2, 2) * (7.189819 * x - 4.5949095) + 2) / 2;
        default:
            return 0;
    }
}

Back

1.2，WinForm效果

a，EaseIn：

b，EaseOut：

c，EaseInOut：

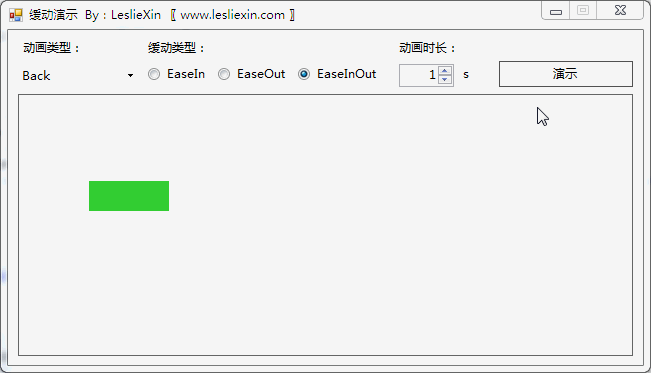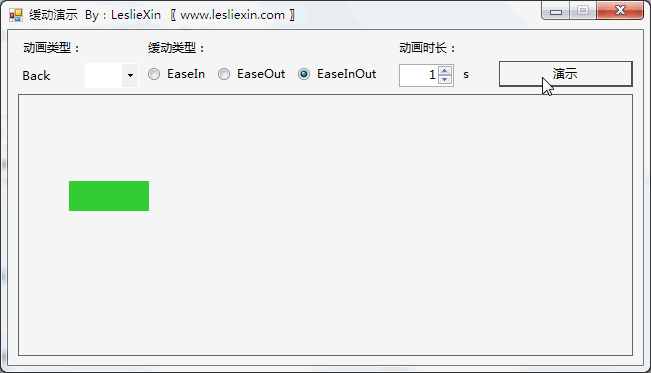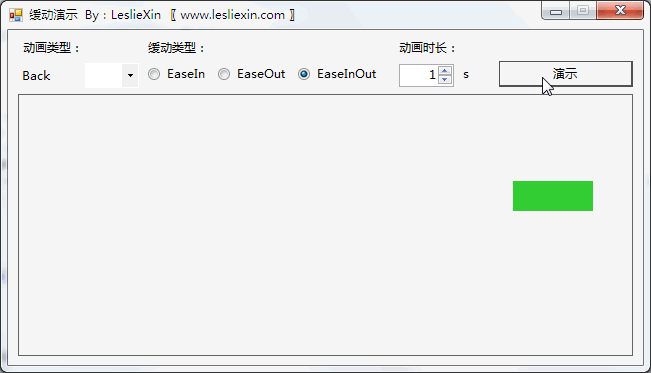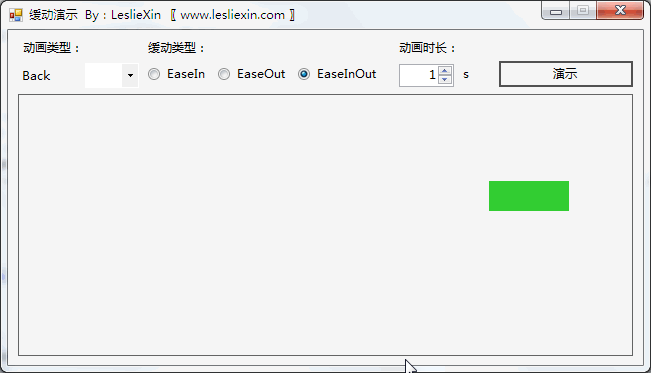
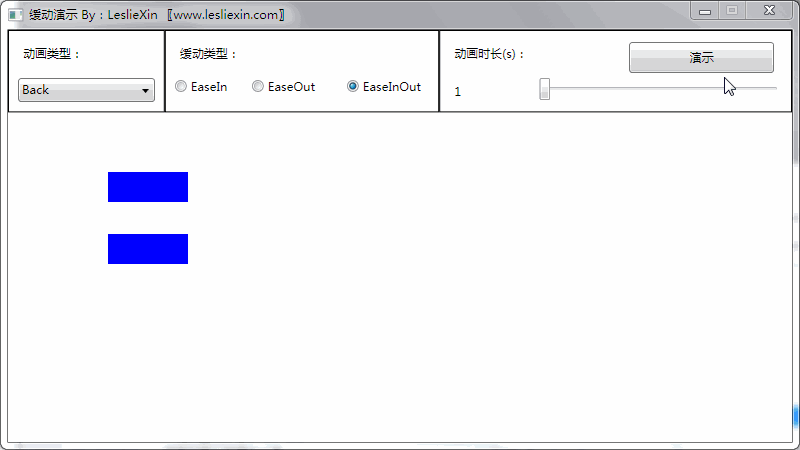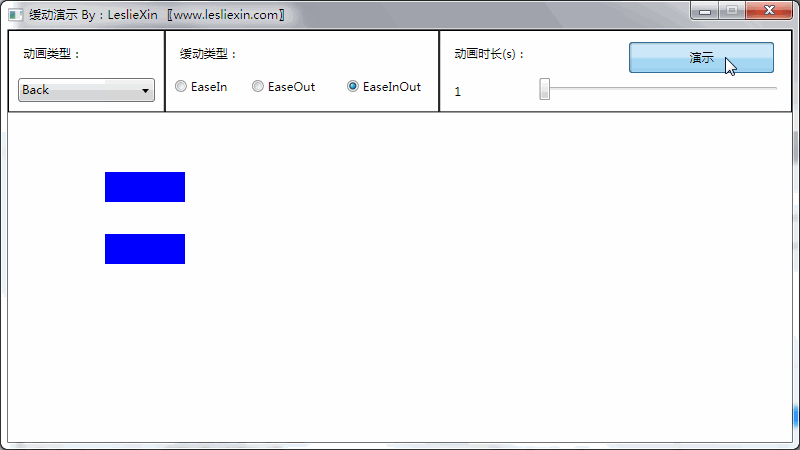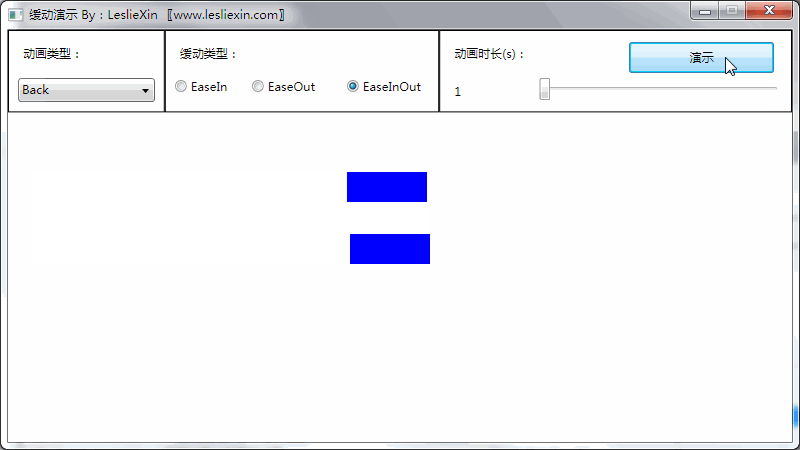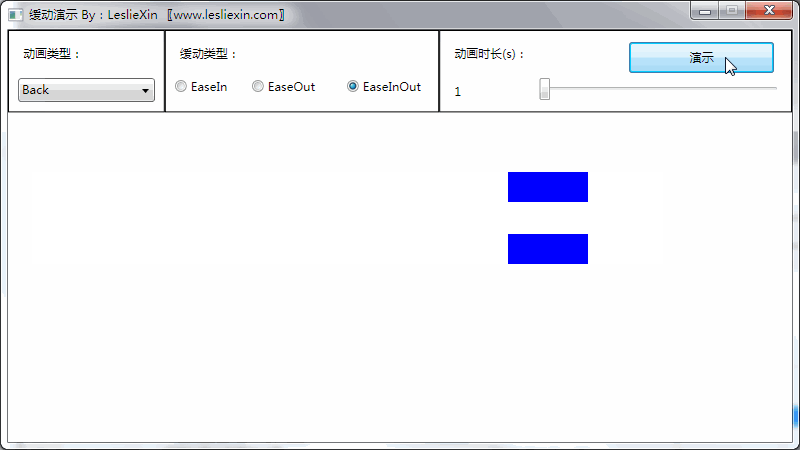
1.3，WPF效果

（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

b，EaseOut：

c，EaseInOut：

2，Bounce

曲线（图源自MSDN）：

2.1，曲线公式

private static double BounceOut(double x)
{
    if (x < 1d / 2.75d) return 7.5625 * x * x;
    else if (x < 2d / 2.75d) return 7.5625 * (x -= 1.5d / 2.75d) * x + 0.75;
    else if(x<2.5d/2.75d) return 7.5625 * (x -= 2.25d / 2.75d) * x + 0.9375;
    else return 7.5625 * (x -= 2.625d / 2.75d) * x + 0.984375;
}

public static double Bounce(double x, LEaseMode easeMode)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return 1 - BounceOut(1 - x);
        case LEaseMode.EaseOut:
            return BounceOut(x);
        case LEaseMode.EaseInOut:
            return x < 0.5 ? (1 - BounceOut(1 - 2 * x)) / 2 : (1 + BounceOut(2 * x - 1)) / 2;
        default:
            return 0;
    }
}

Bounce

2.2，WinForm效果

a，EaseIn：

b，EaseOut：

c，EaseInOut：

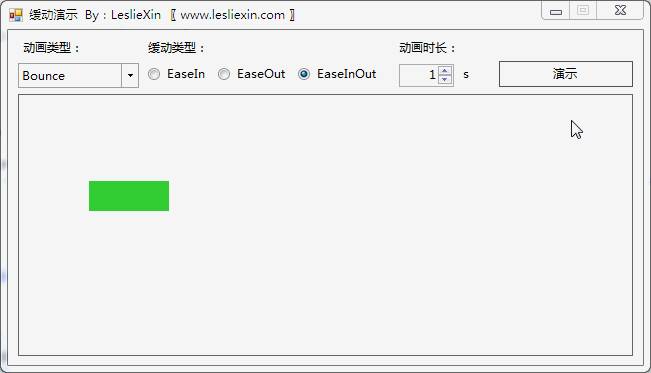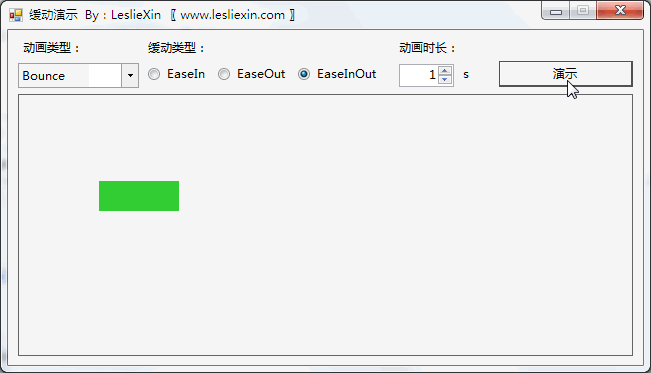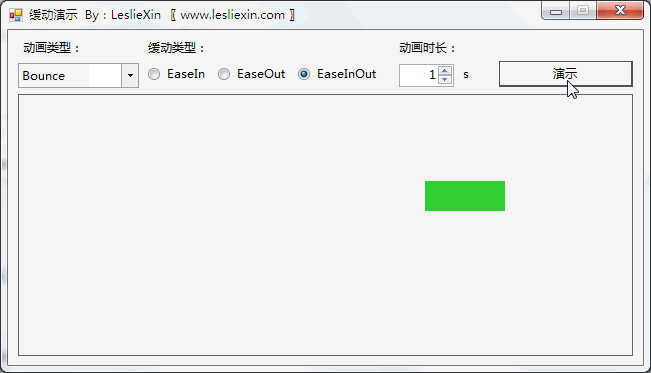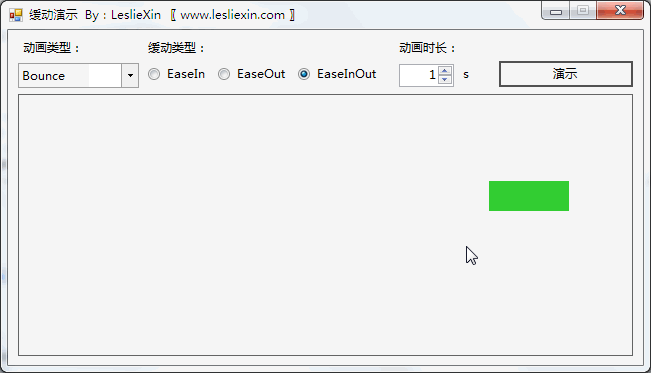
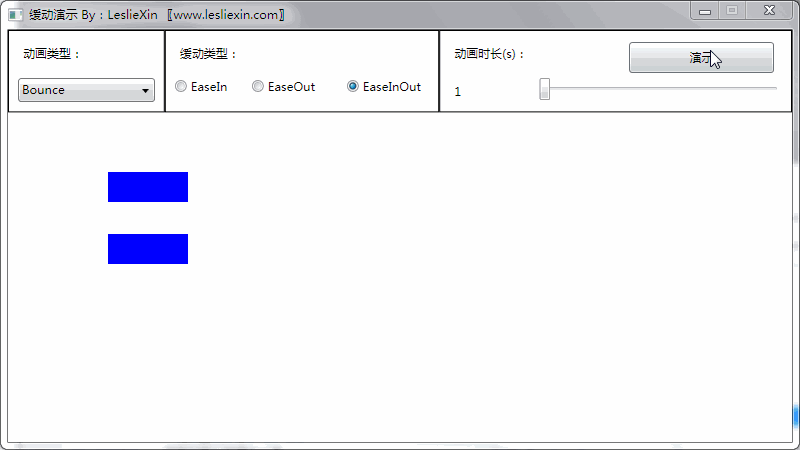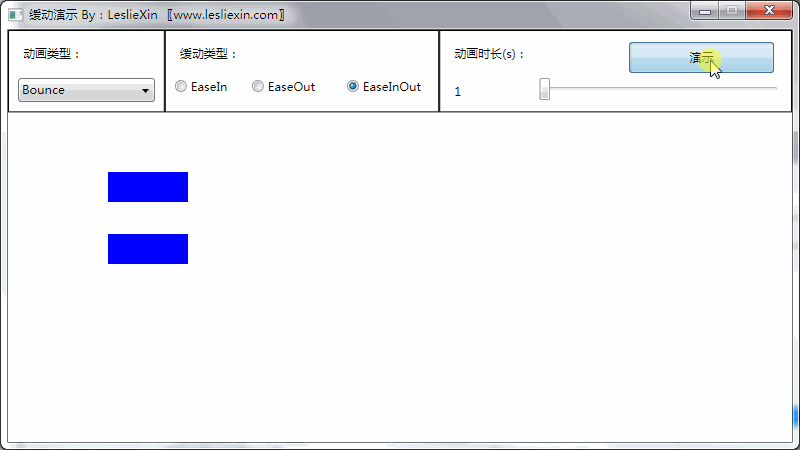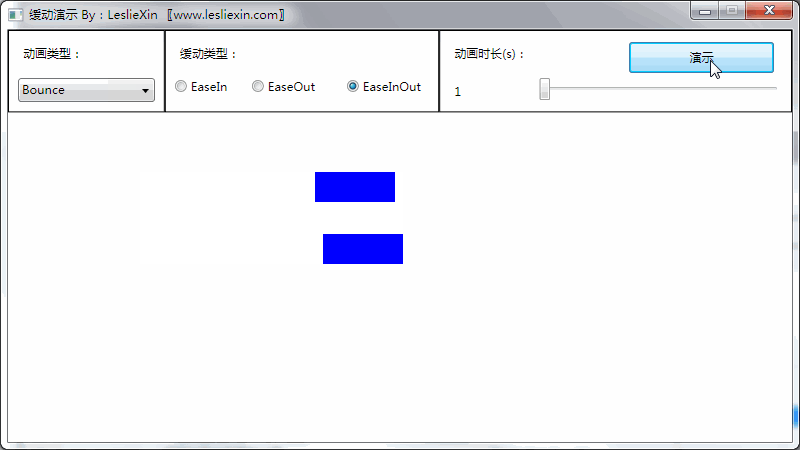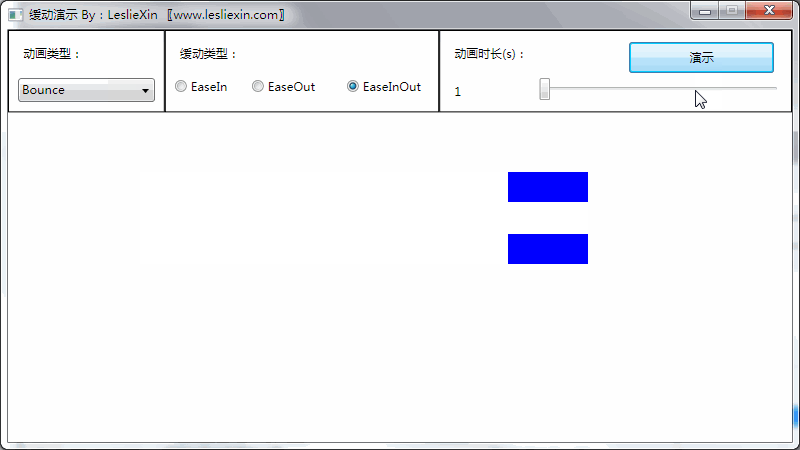
2.3，WPF效果

（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

b，EaseOut：

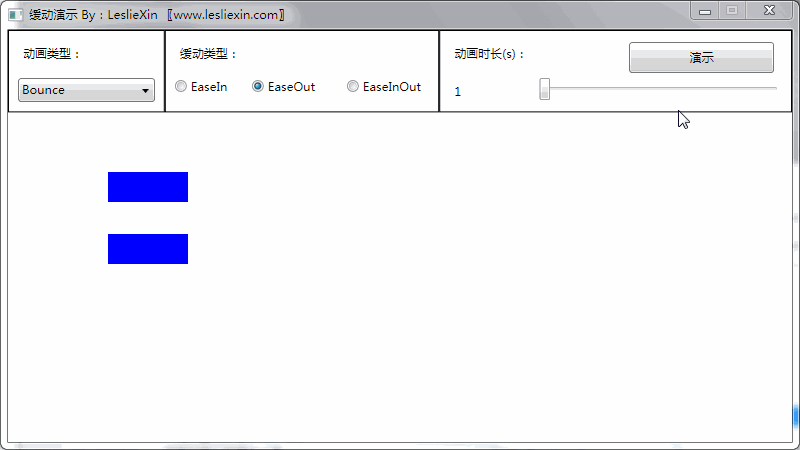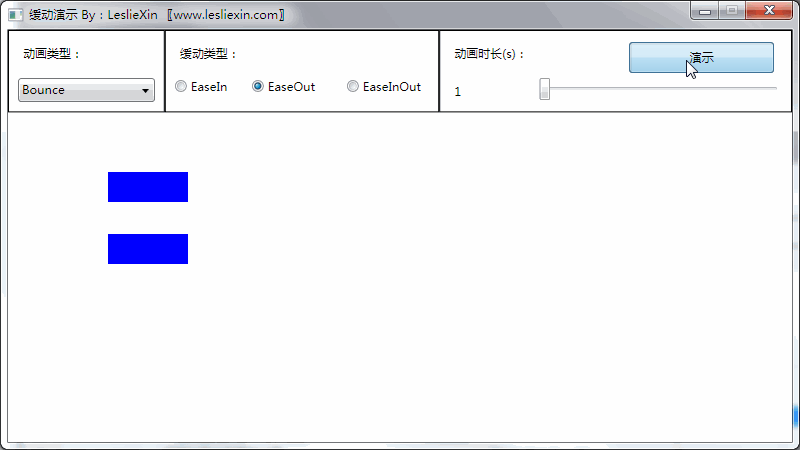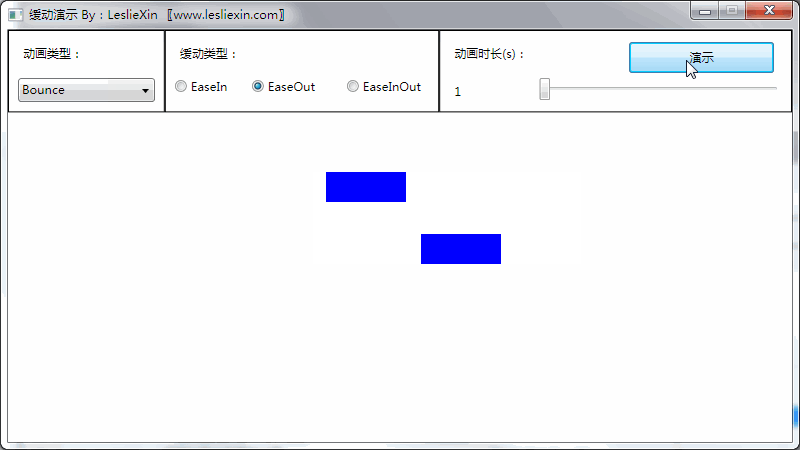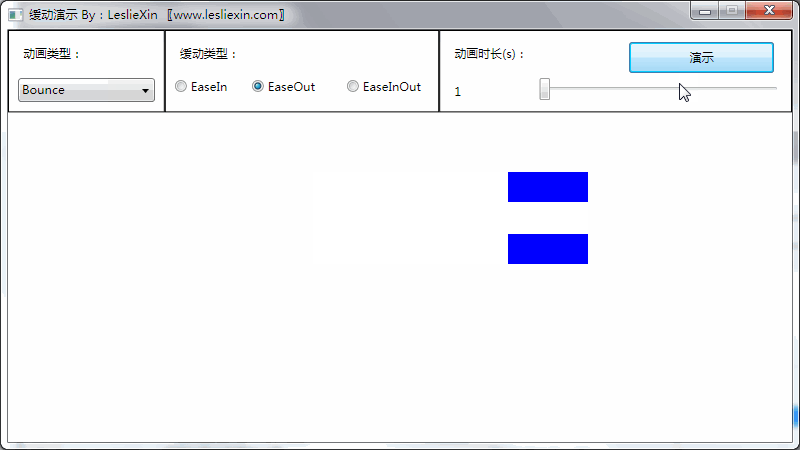
c，EaseInOut：

3，Circle

曲线（图源自MSDN）：

3.1，曲线公式

public static double Circle(double x, LEaseMode easeMode)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return 1 - Math.Sqrt(1 - Math.Pow(x, 2));
        case LEaseMode.EaseOut:
            return Math.Sqrt(1 - Math.Pow(x - 1, 2));
        case LEaseMode.EaseInOut:
            return x < 0.5 ? (1 - Math.Sqrt(1 - Math.Pow(2 * x, 2))) / 2 : (Math.Sqrt(1 - Math.Pow(-2 * x + 2, 2)) + 1) / 2;
        default:
            return 0;
    }
}

Circle

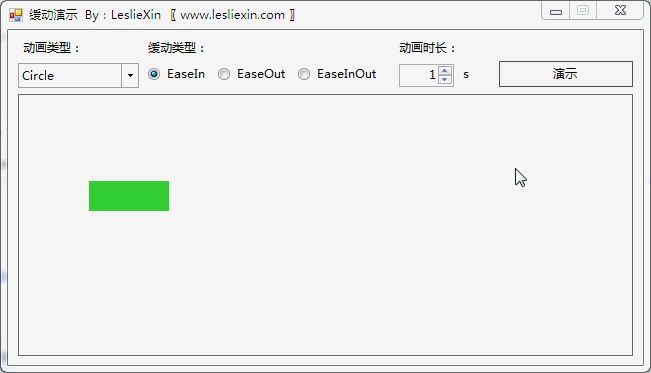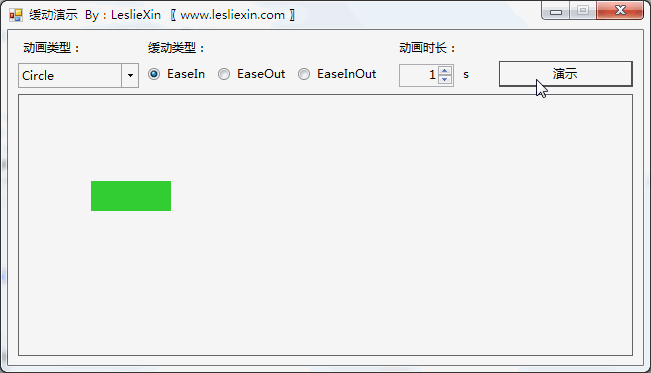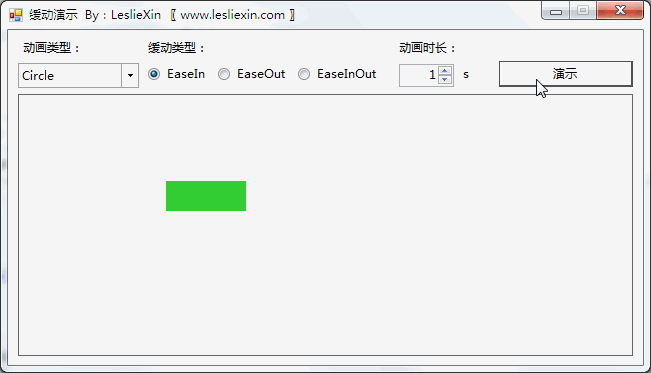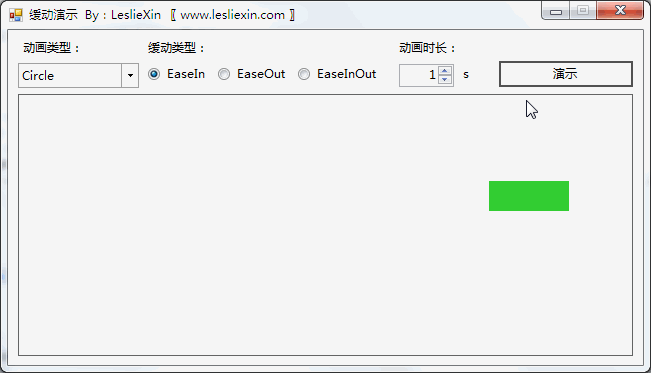
3.2，WinForm效果

a，EaseIn：

b，EaseOut：

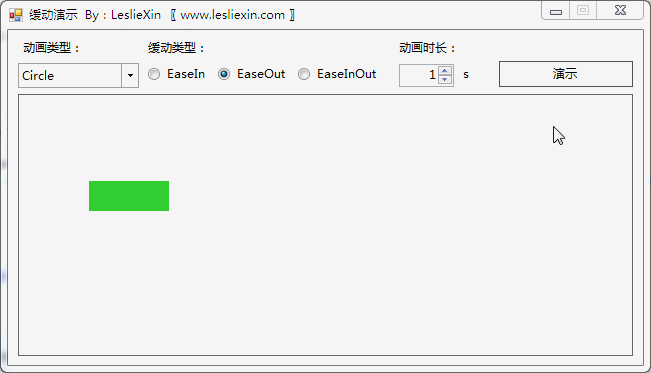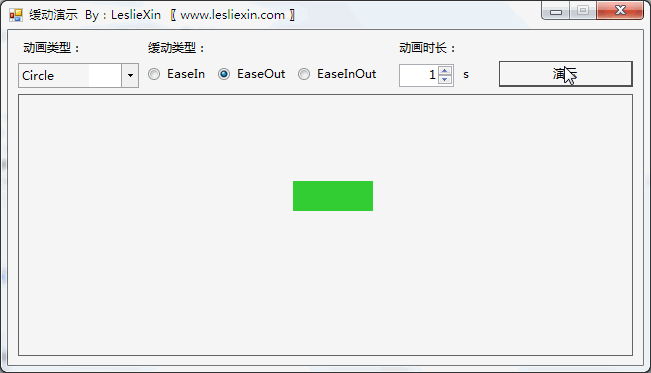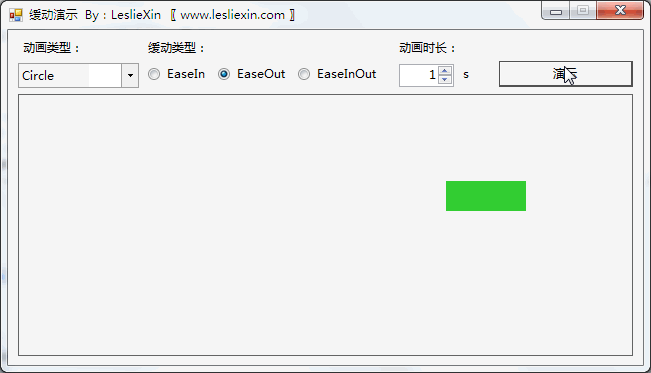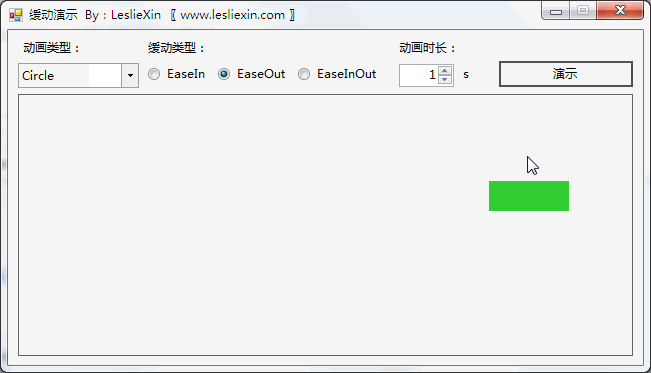
c，EaseInOut：

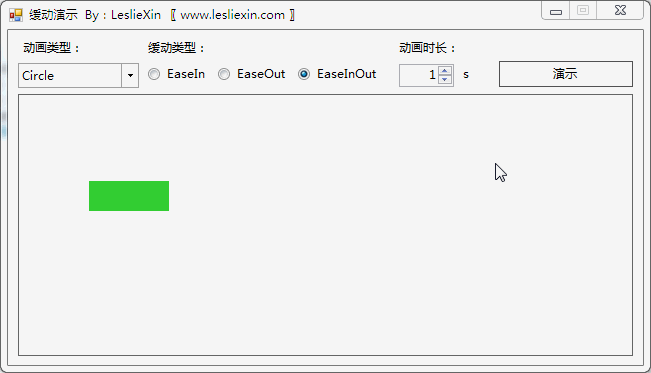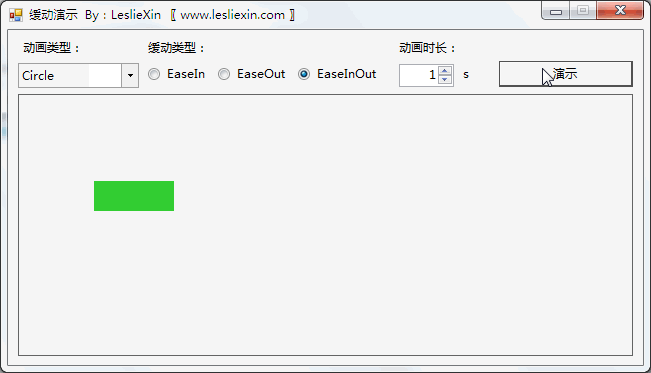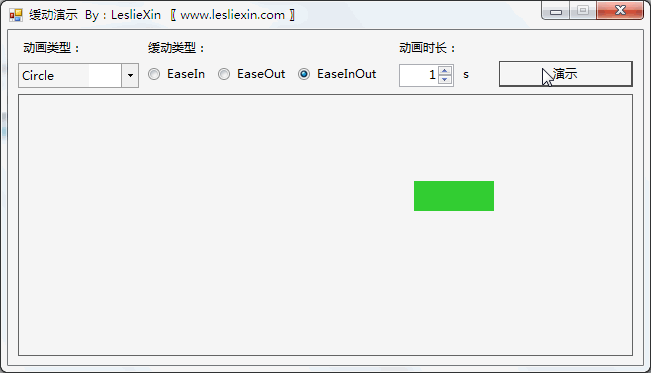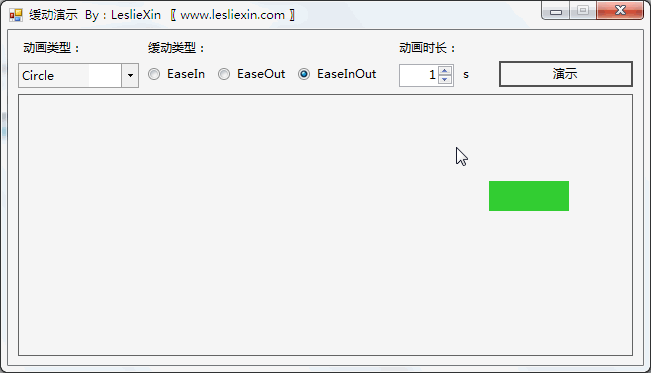
3.3，WPF效果

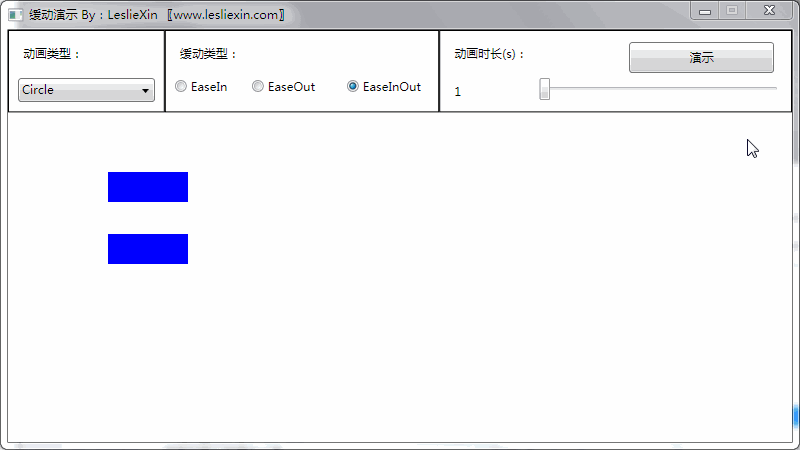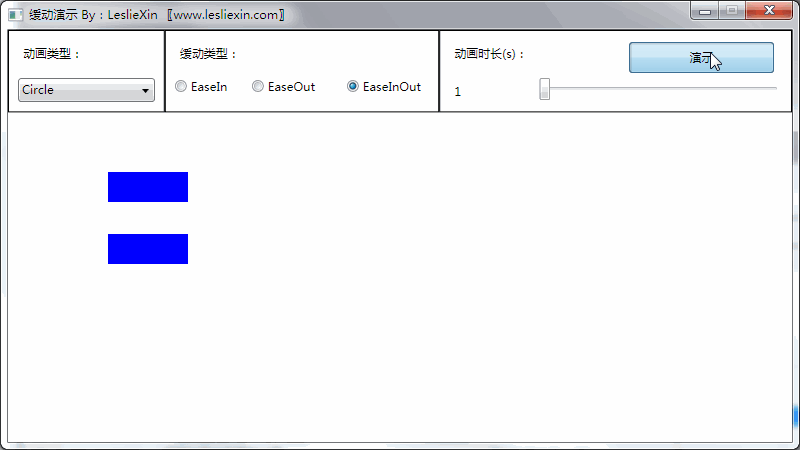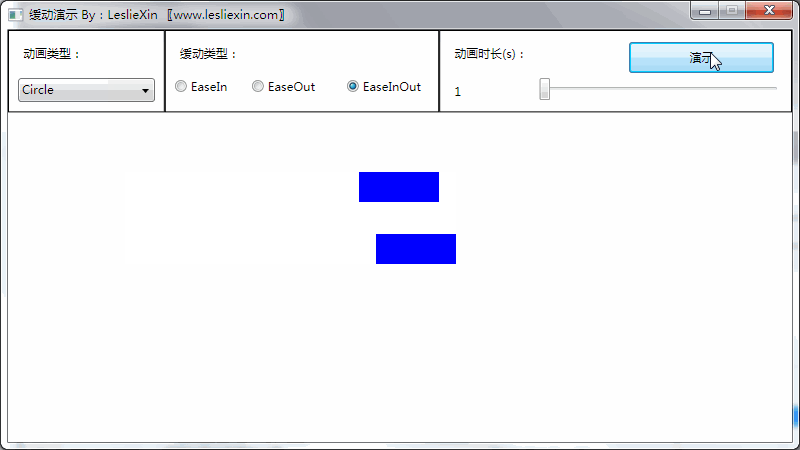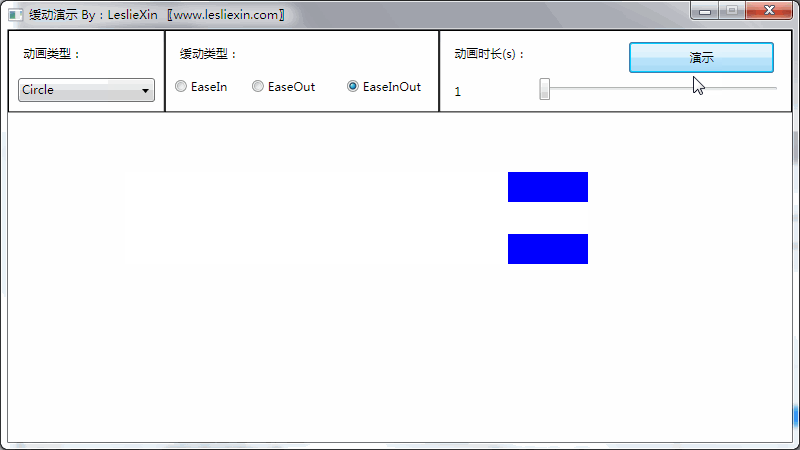
（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

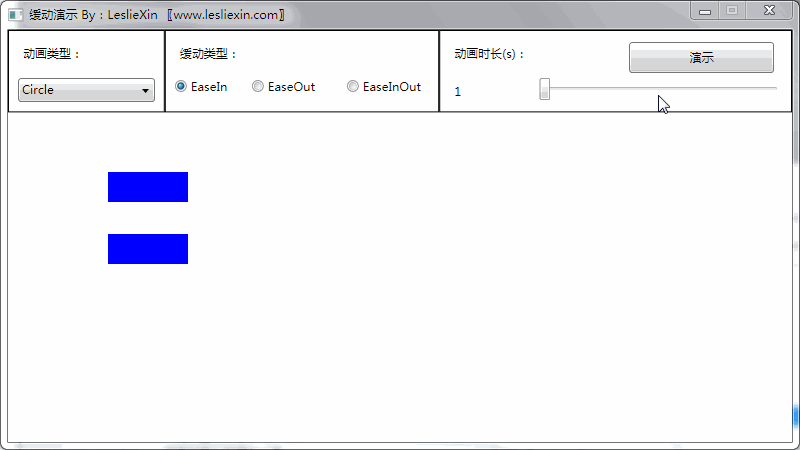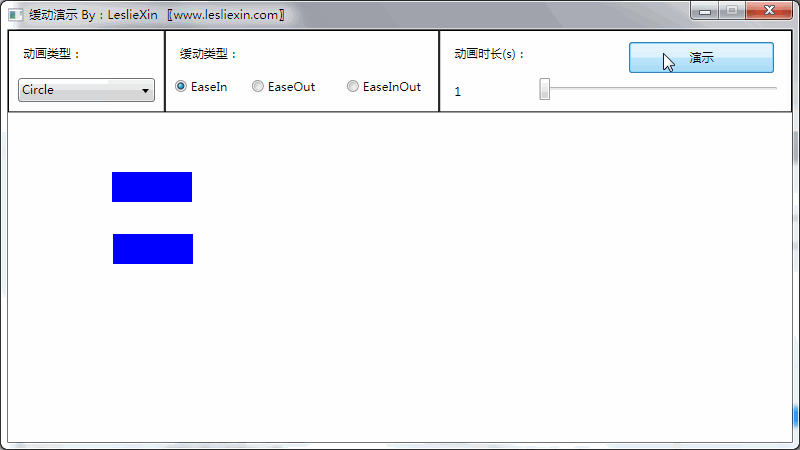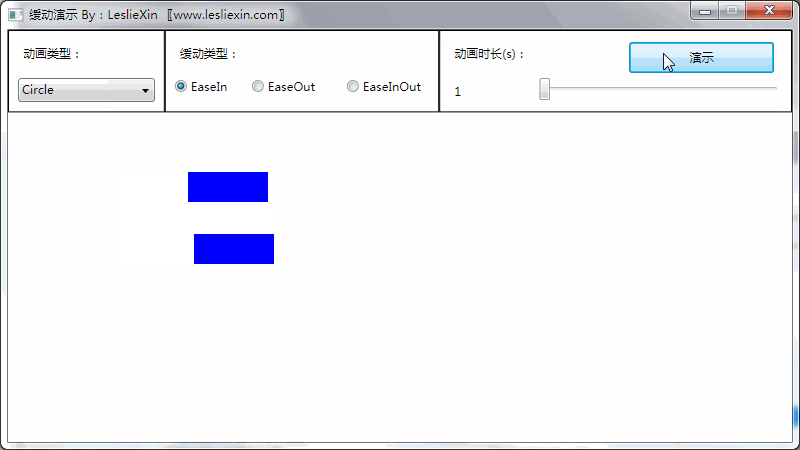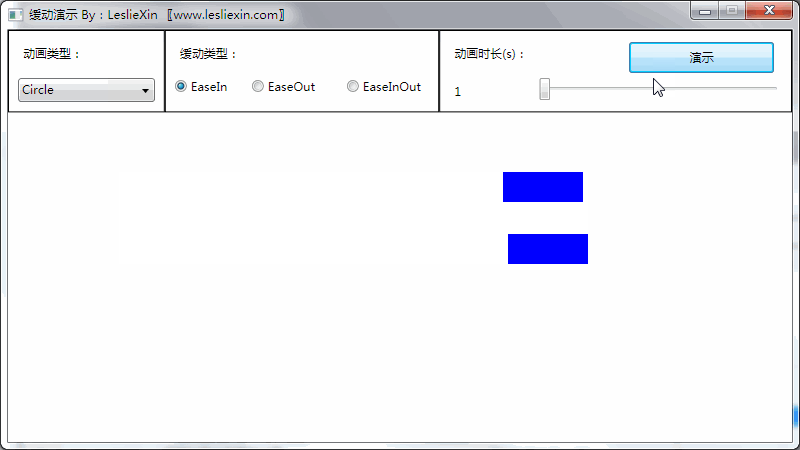
b，EaseOut：

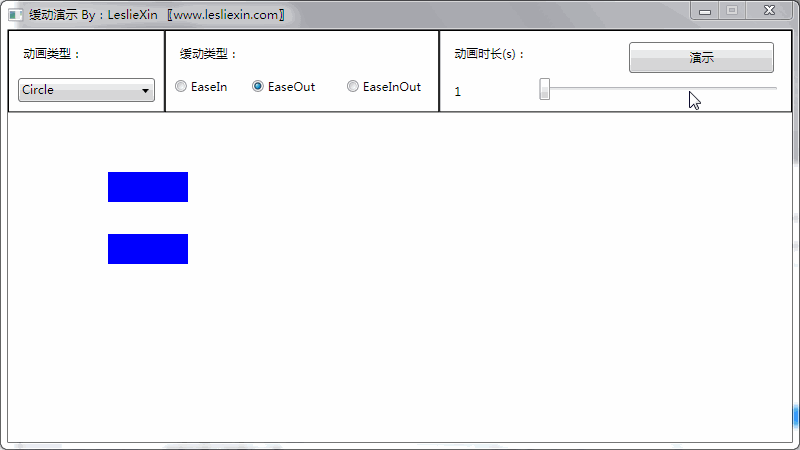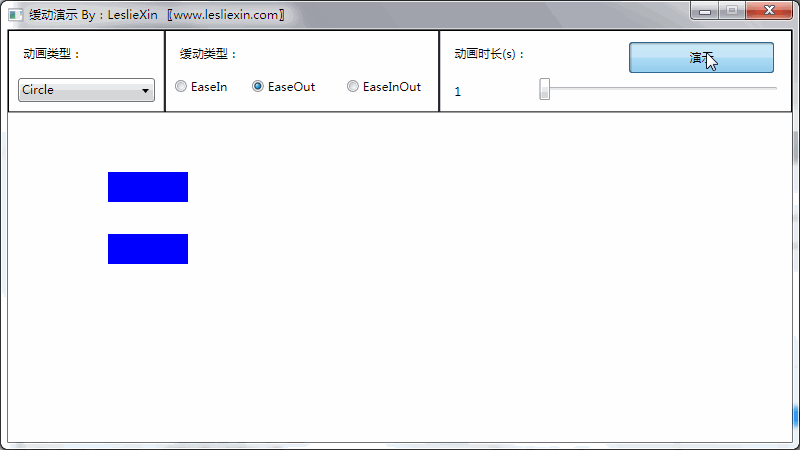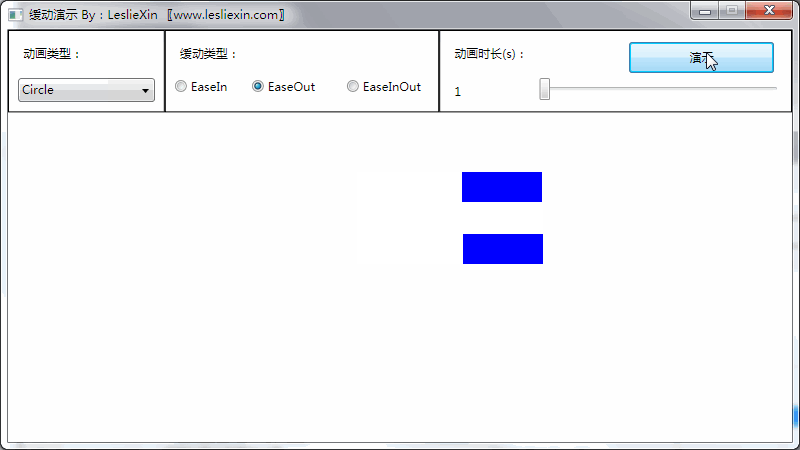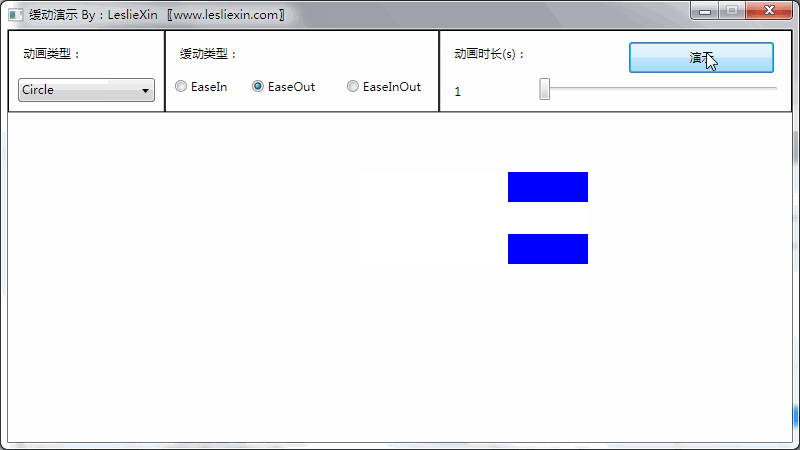
c，EaseInOut：

4，Quadratic

曲线（图源自MSDN）：

4.1，曲线公式

public static double Power(double x,LEaseMode easeMode,int power)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return Math.Pow(x, power);
        case LEaseMode.EaseOut:
            return 1-Math.Pow(1-x,power);
        case LEaseMode.EaseInOut:
            return x < 0.5 ? Math.Pow(2,power-1)*Math.Pow(x,power) : 1 - Math.Pow(-2 * x + 2, power) / 2;
        default:
            return 0;
    }
}

public static double Quadratic(double x, LEaseMode easeMode)
{
    return Power(x, easeMode, 2);
}

Quadratic

4.2，WinForm效果

a，EaseIn：

b，EaseOut：

c，EaseInOut：

4.3，WPF效果

（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

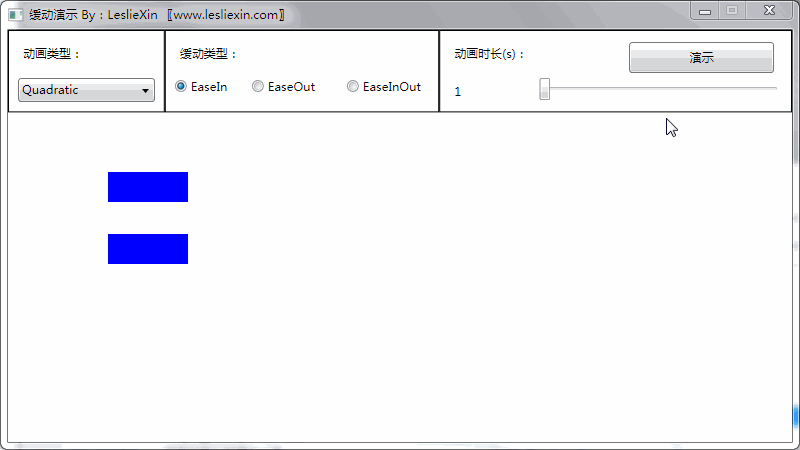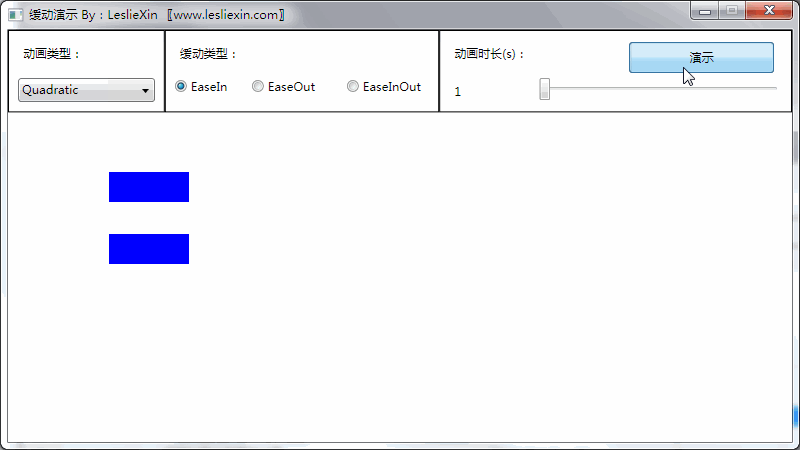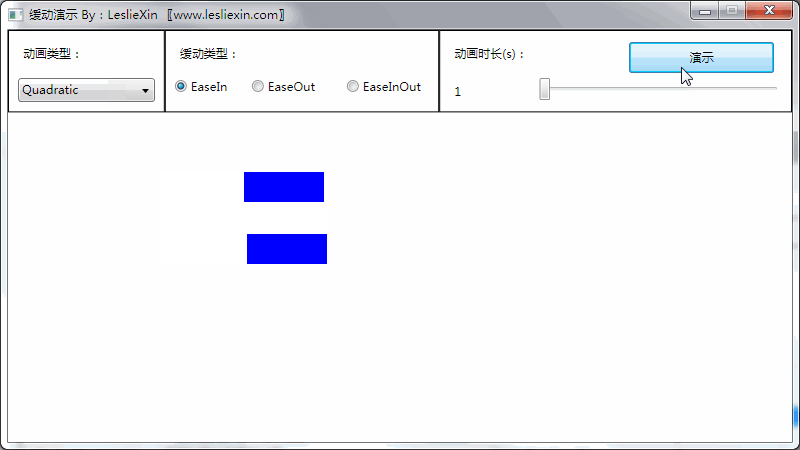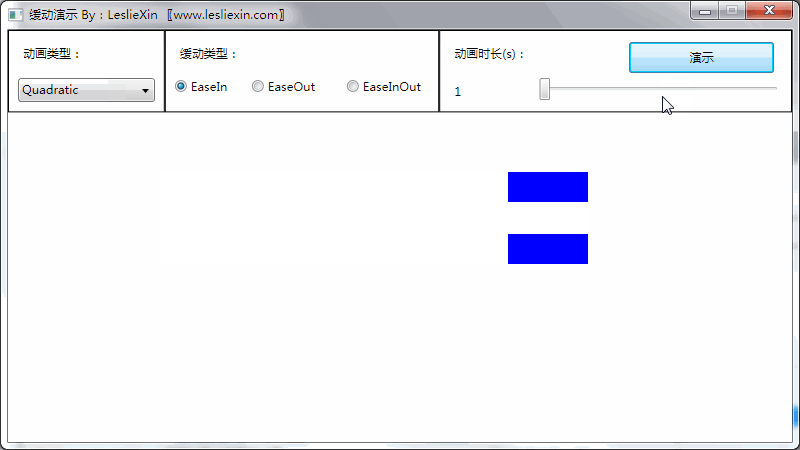
b，EaseOut：

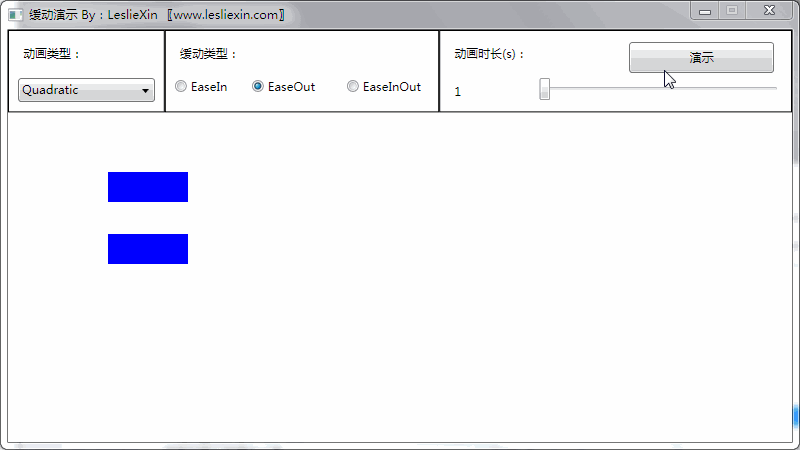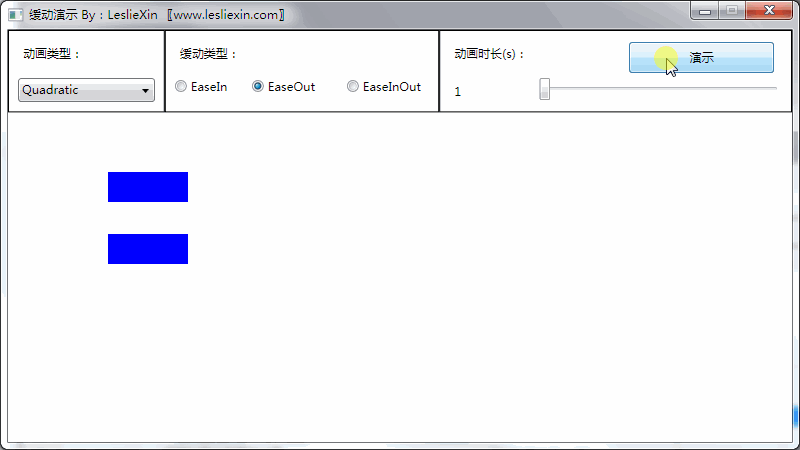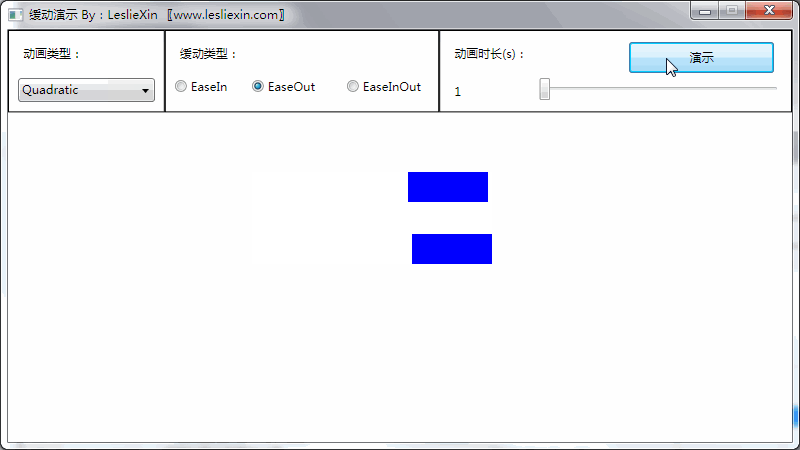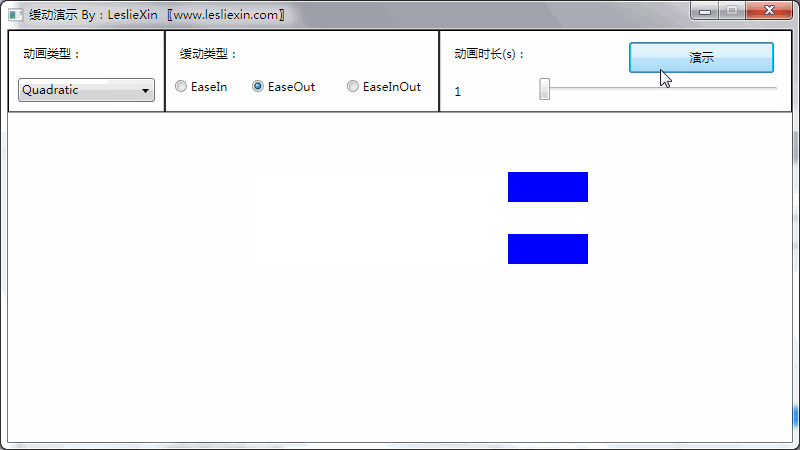
c，EaseInOut：

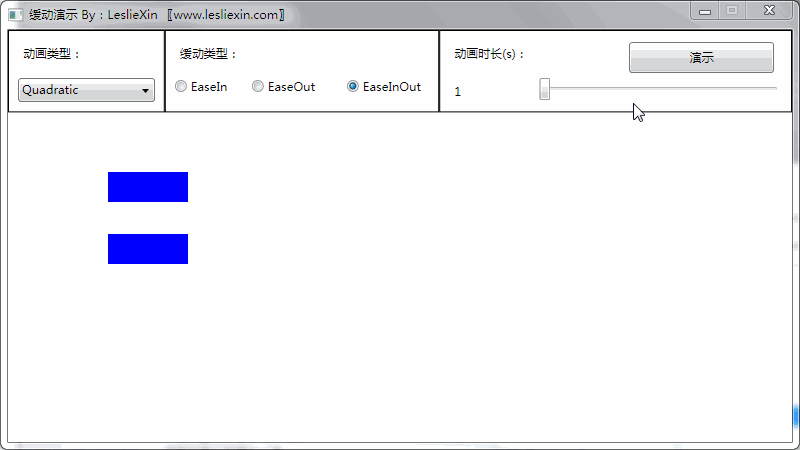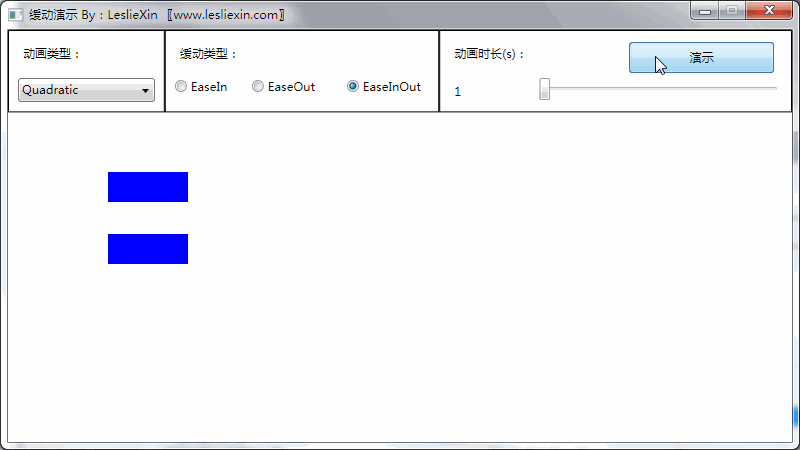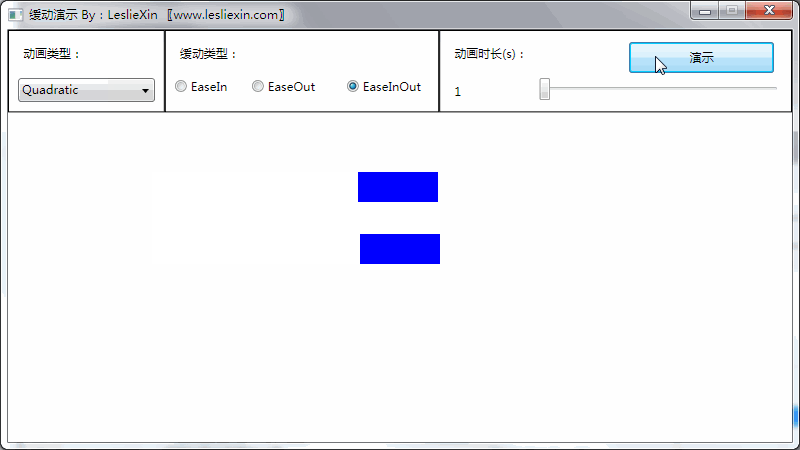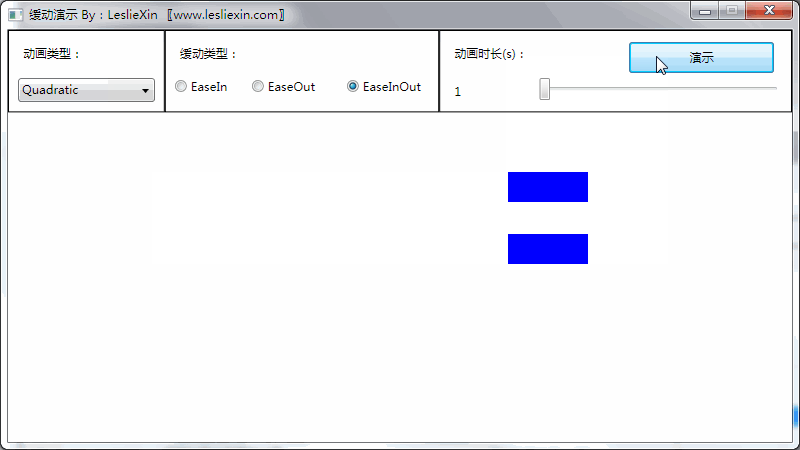
5，Cubic

曲线（图源自MSDN）：

5.1，曲线公式

public static double Power(double x,LEaseMode easeMode,int power)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return Math.Pow(x, power);
        case LEaseMode.EaseOut:
            return 1-Math.Pow(1-x,power);
        case LEaseMode.EaseInOut:
            return x < 0.5 ? Math.Pow(2,power-1)*Math.Pow(x,power) : 1 - Math.Pow(-2 * x + 2, power) / 2;
        default:
            return 0;
    }
}

public static double Cubic(double x, LEaseMode easeMode)
{
    return Power(x, easeMode, 3);
}

Cubic

5.2，WinForm效果

a，EaseIn：

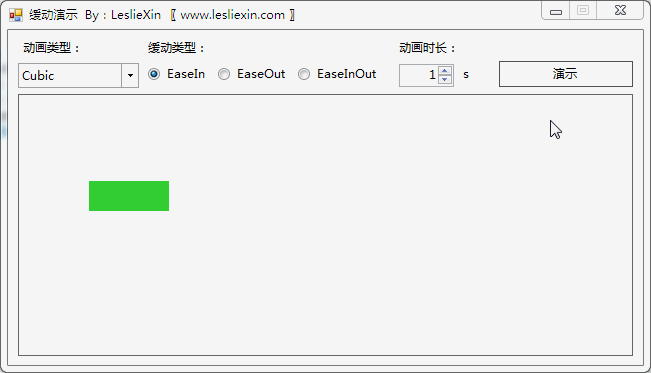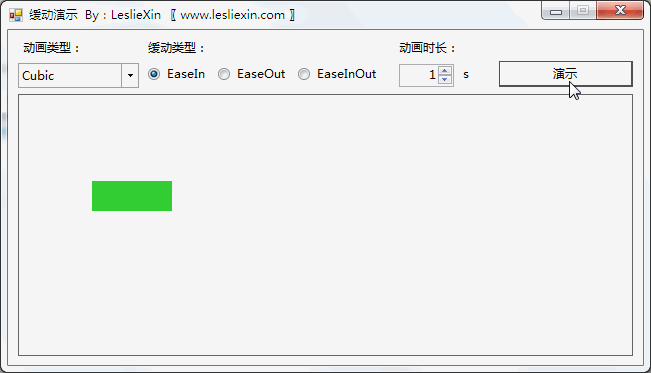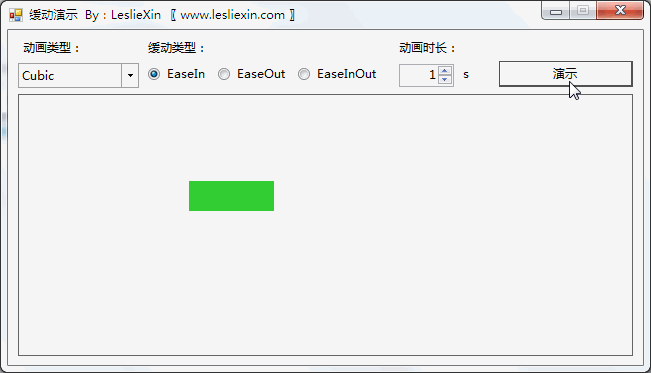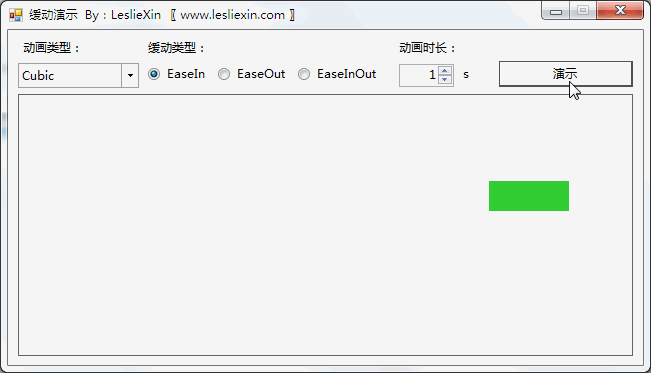
b，EaseOut：

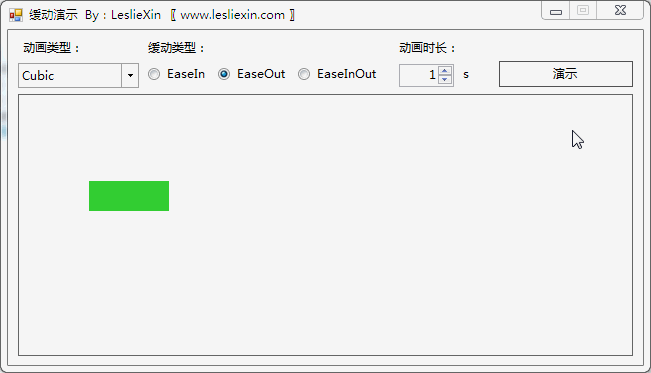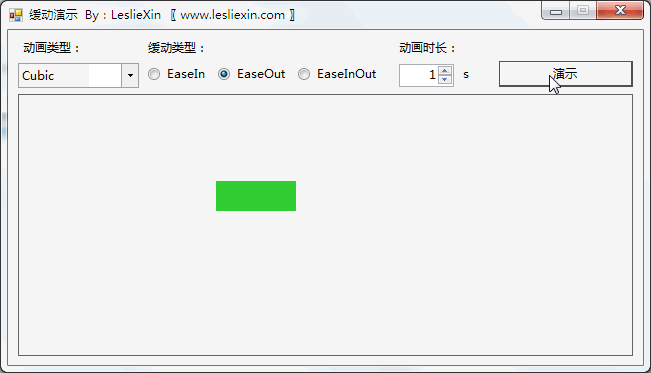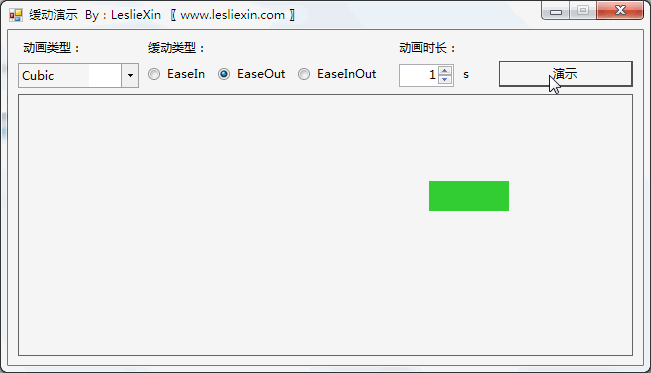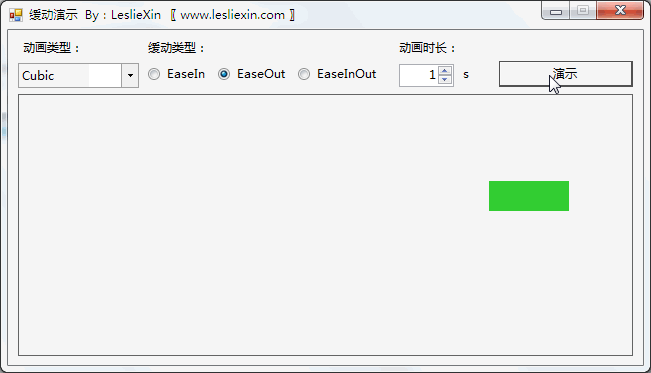
c，EaseInOut：

5.3，WPF效果

（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

b，EaseOut：

c，EaseInOut：

6，Quartic

曲线（图源自MSDN）：

6.1，曲线公式

public static double Power(double x,LEaseMode easeMode,int power)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return Math.Pow(x, power);
        case LEaseMode.EaseOut:
            return 1-Math.Pow(1-x,power);
        case LEaseMode.EaseInOut:
            return x < 0.5 ? Math.Pow(2,power-1)*Math.Pow(x,power) : 1 - Math.Pow(-2 * x + 2, power) / 2;
        default:
            return 0;
    }
}

public static double Quartic(double x, LEaseMode easeMode)
{
    return Power(x, easeMode,4);
}

Quartic

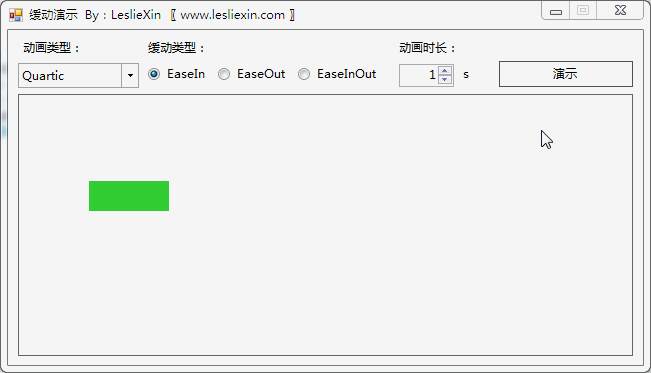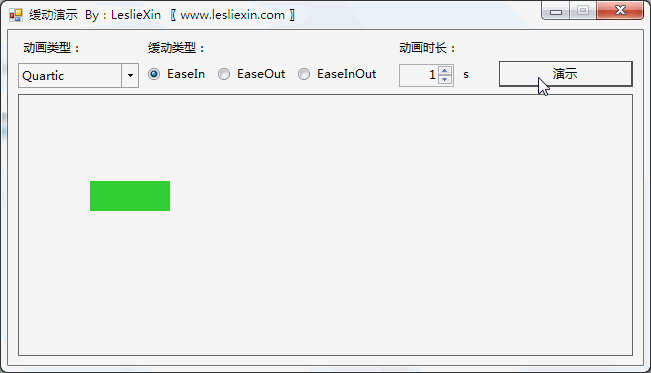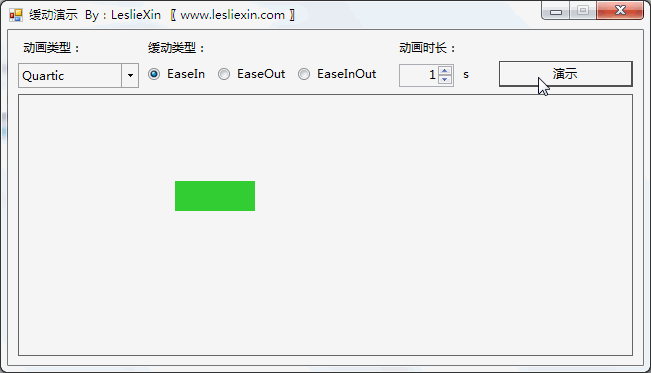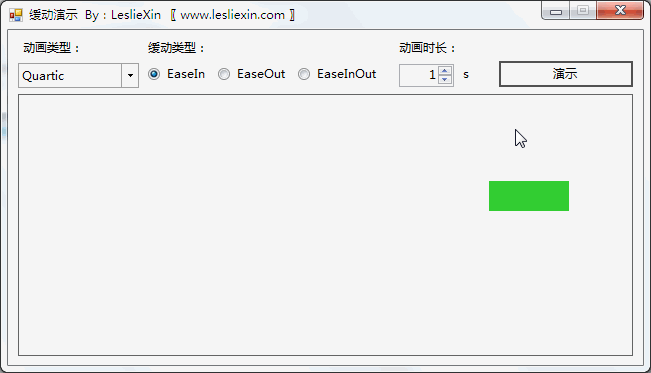
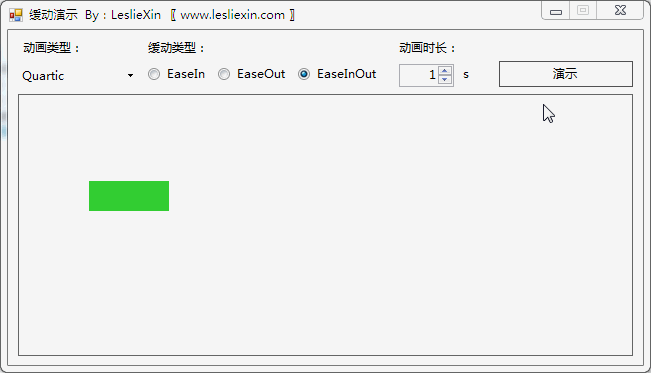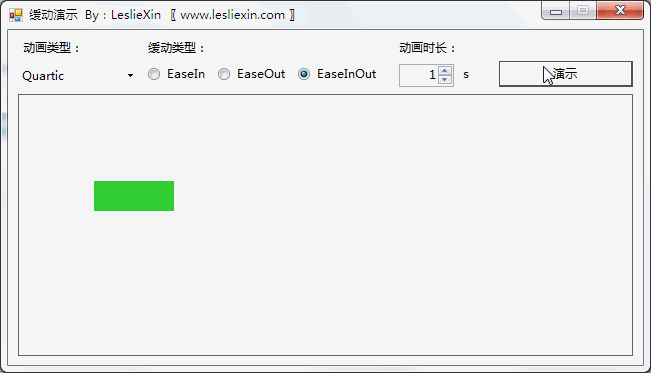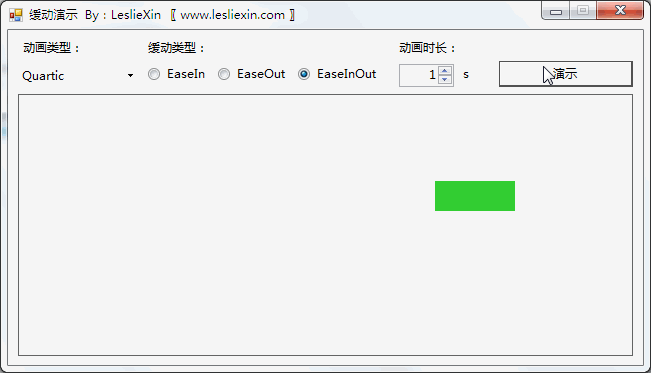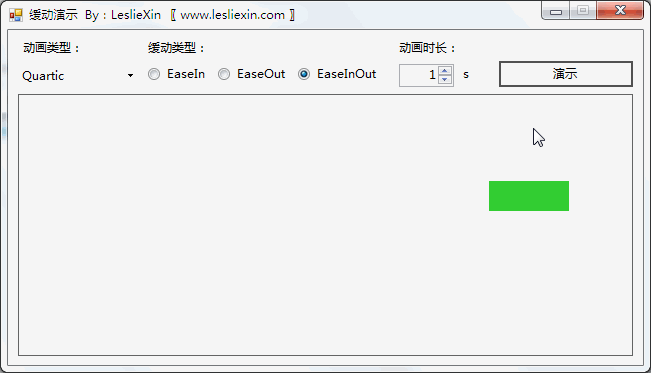
6.2，WinForm效果

a，EaseIn：

b，EaseOut：

c，EaseInOut：

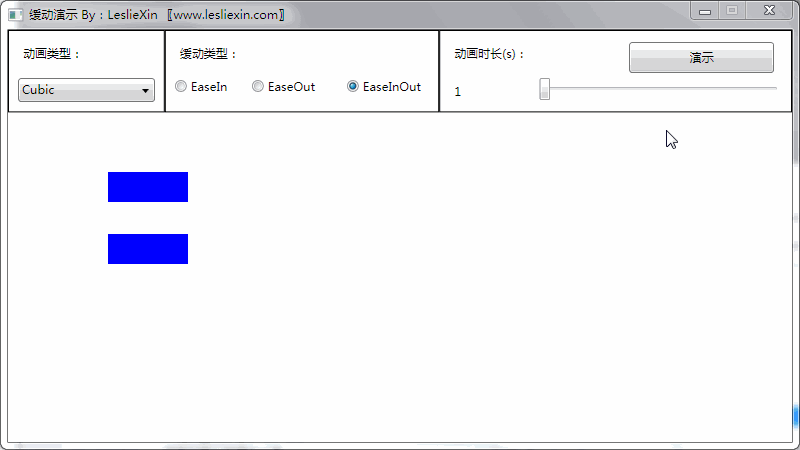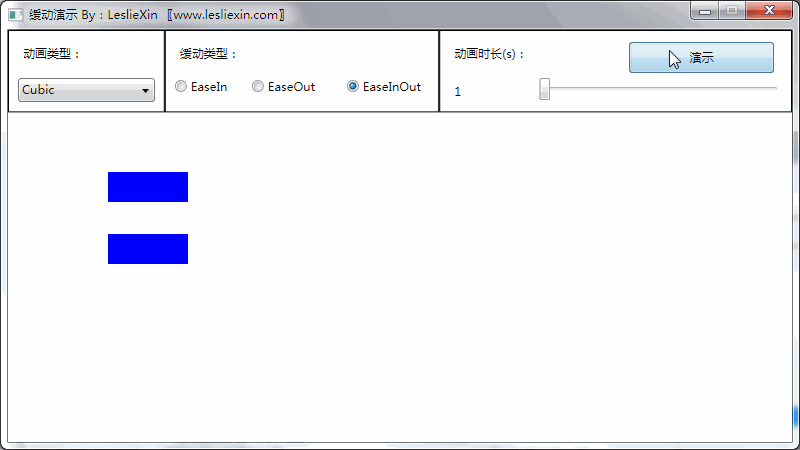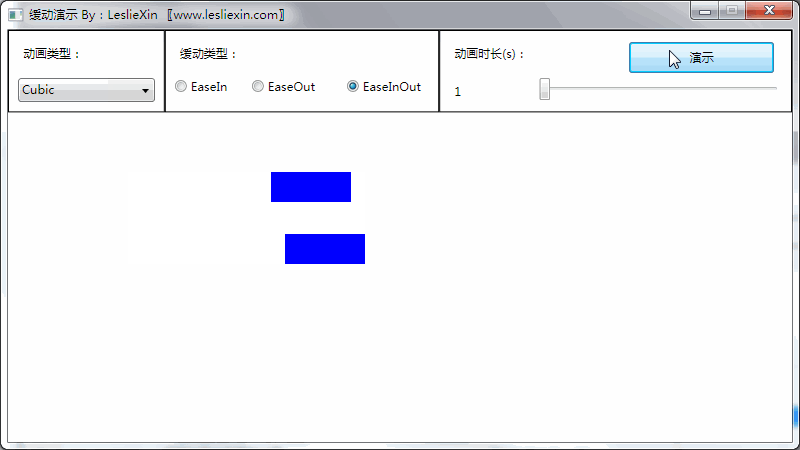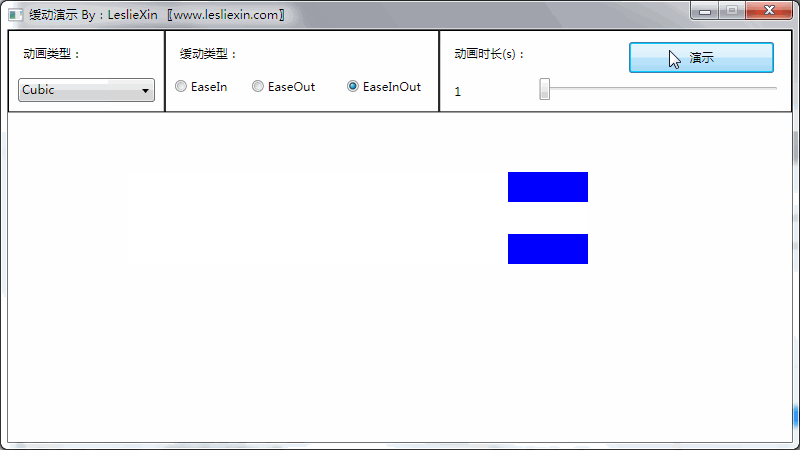
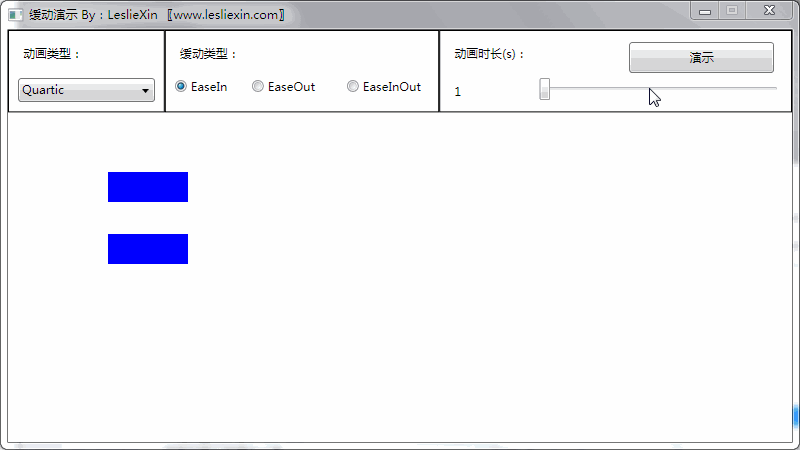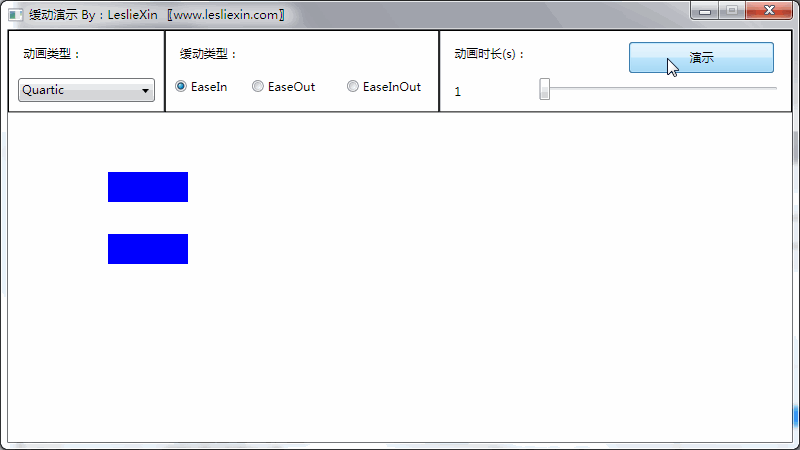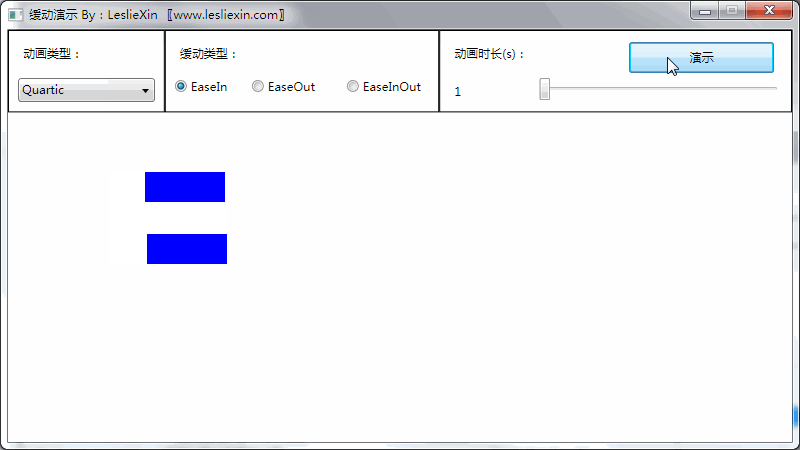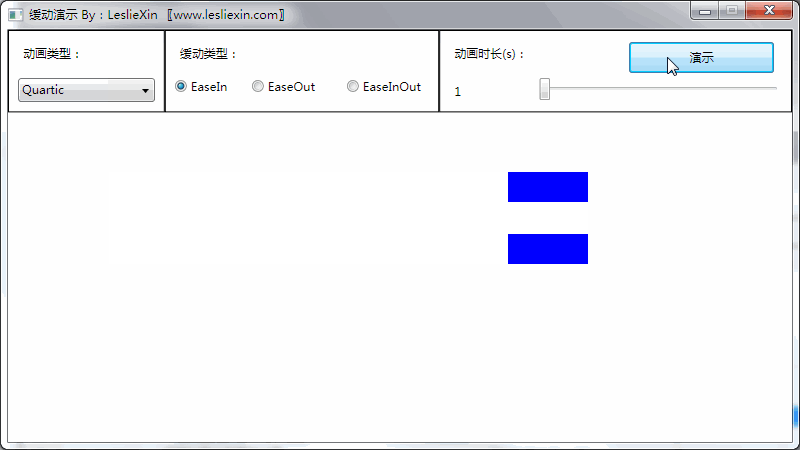
6.3，WPF效果

（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

b，EaseOut：

c，EaseInOut：

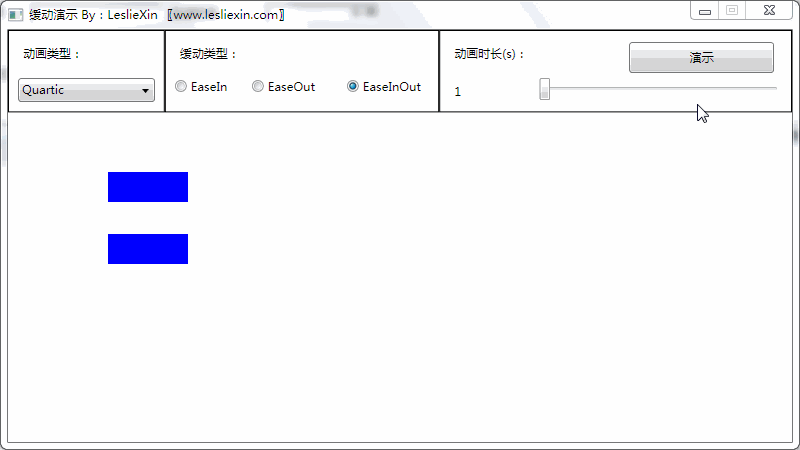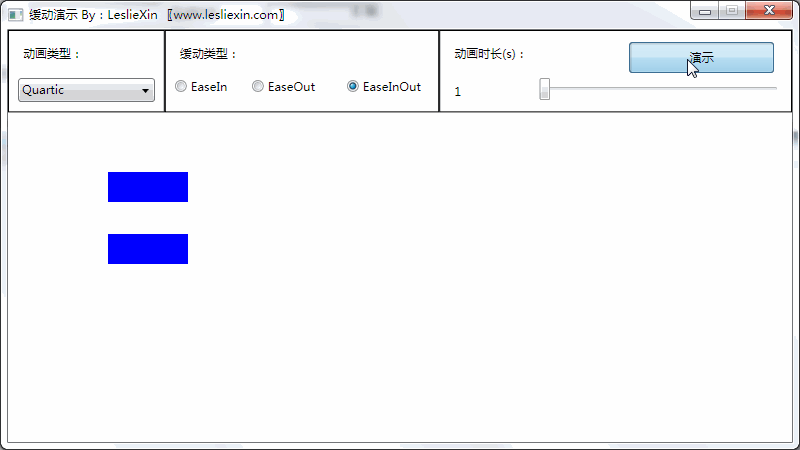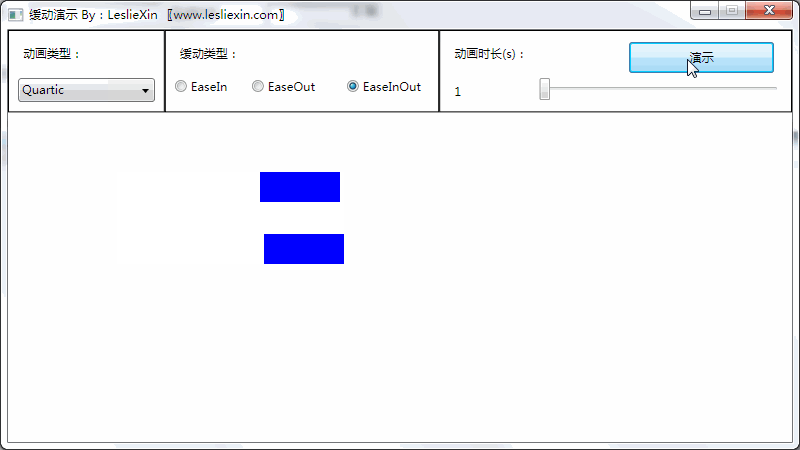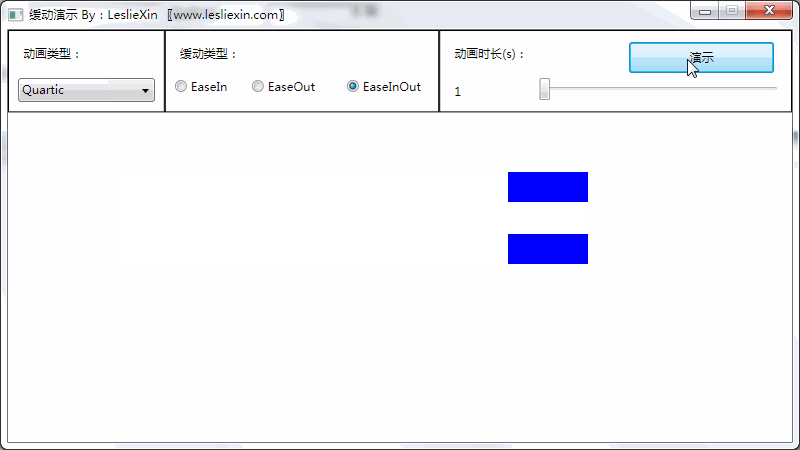
7，Quintic

曲线（图源自MSDN）：

7.1，曲线公式

public static double Power(double x,LEaseMode easeMode,int power)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return Math.Pow(x, power);
        case LEaseMode.EaseOut:
            return 1-Math.Pow(1-x,power);
        case LEaseMode.EaseInOut:
            return x < 0.5 ? Math.Pow(2,power-1)*Math.Pow(x,power) : 1 - Math.Pow(-2 * x + 2, power) / 2;
        default:
            return 0;
    }
}

public static double Quintic(double x, LEaseMode easeMode)
{
    return Power(x, easeMode, 5);
}

Quintic

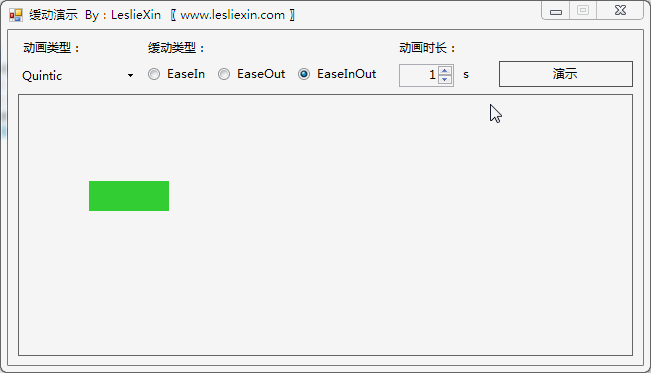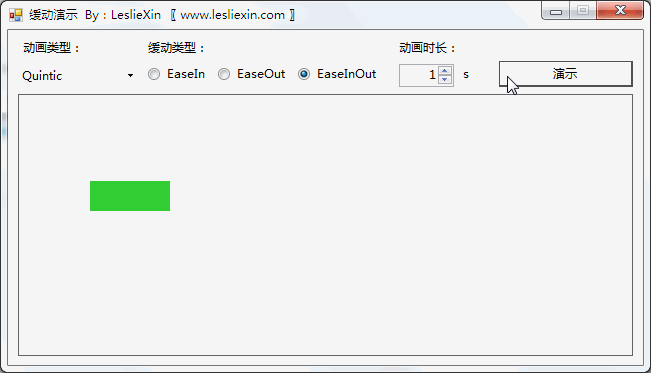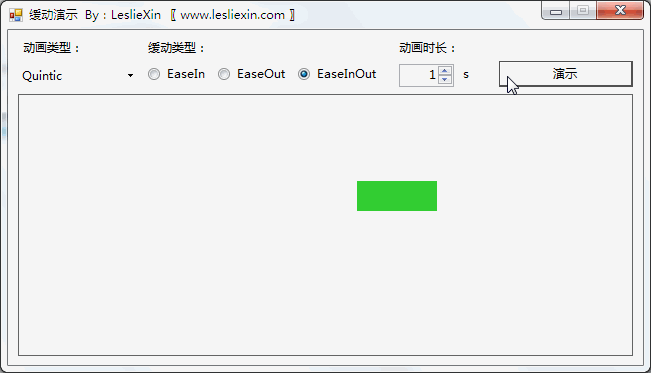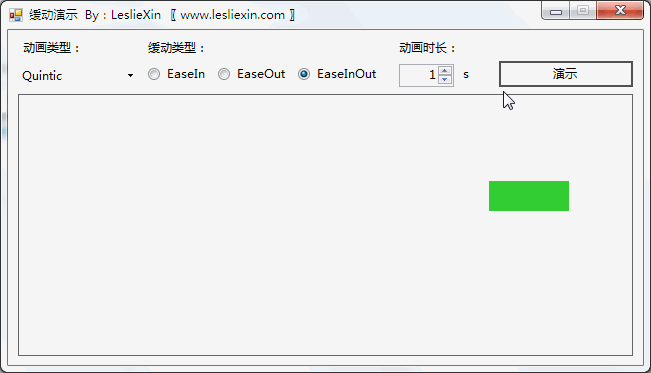
7.2，WinForm效果

a，EaseIn：

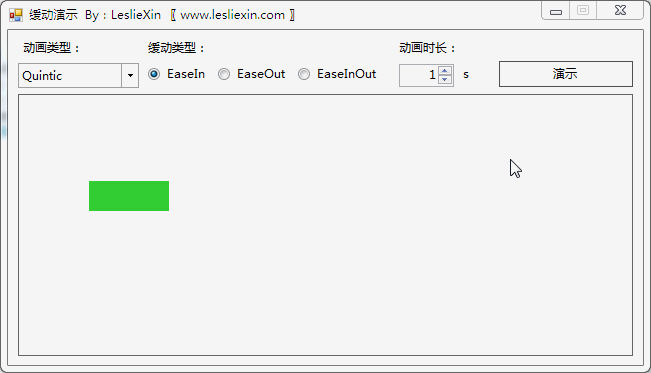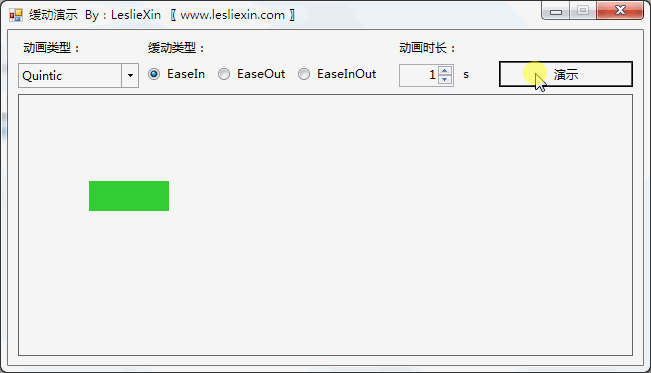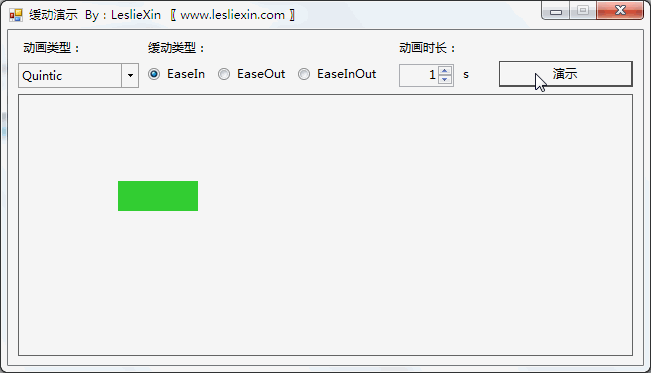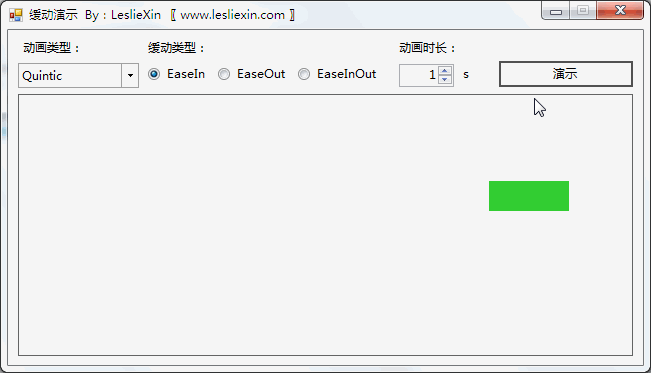
b，EaseOut：

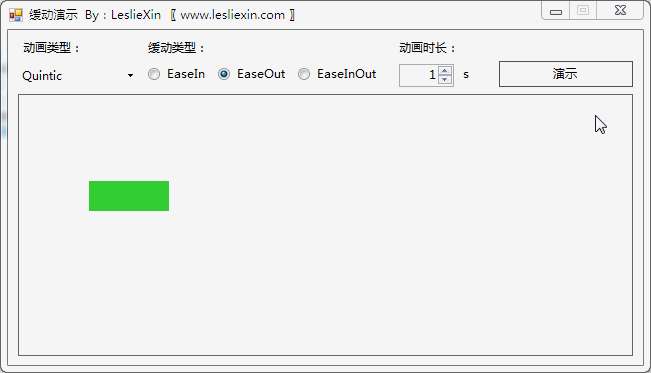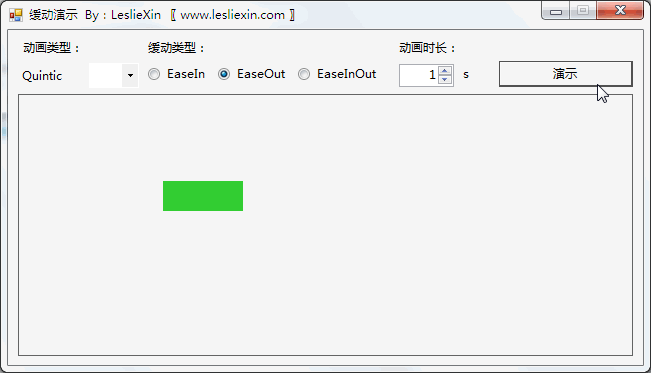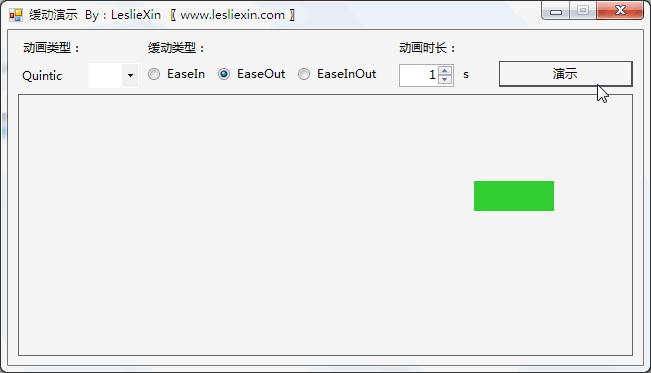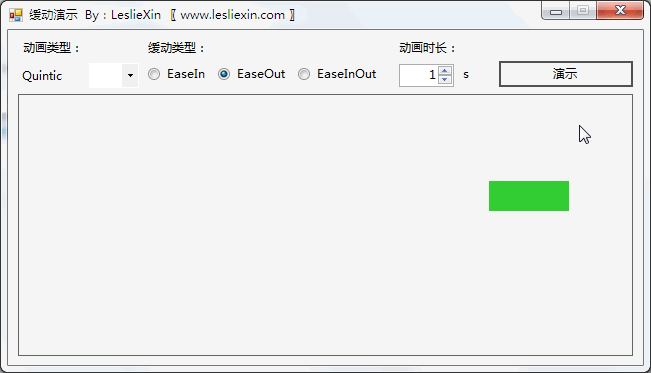
c，EaseInOut：

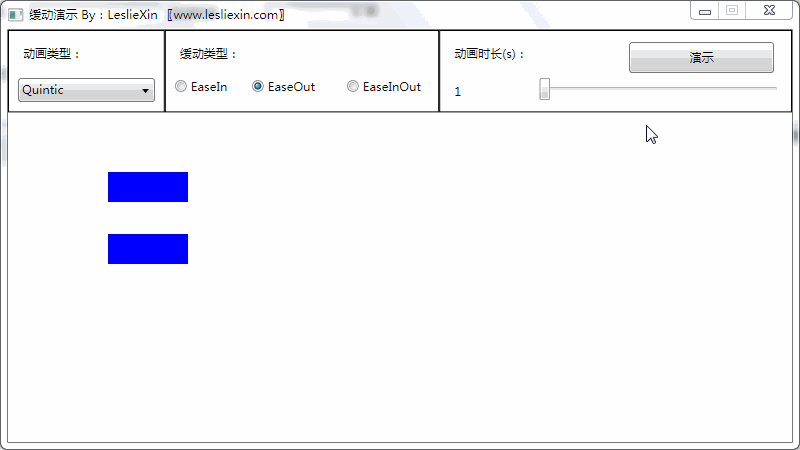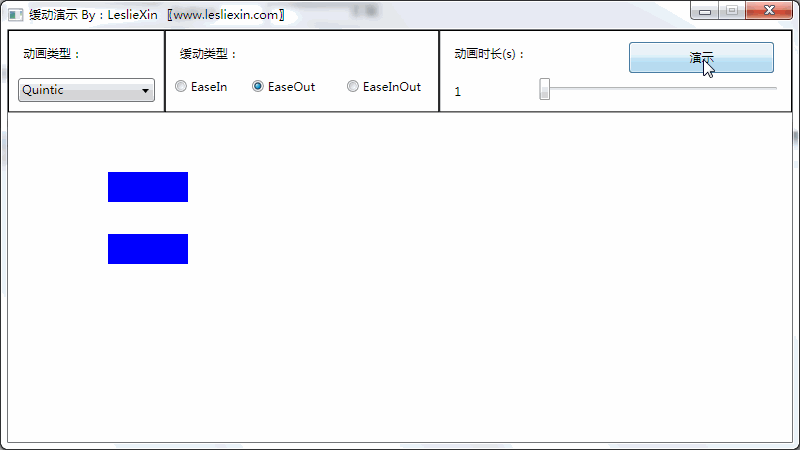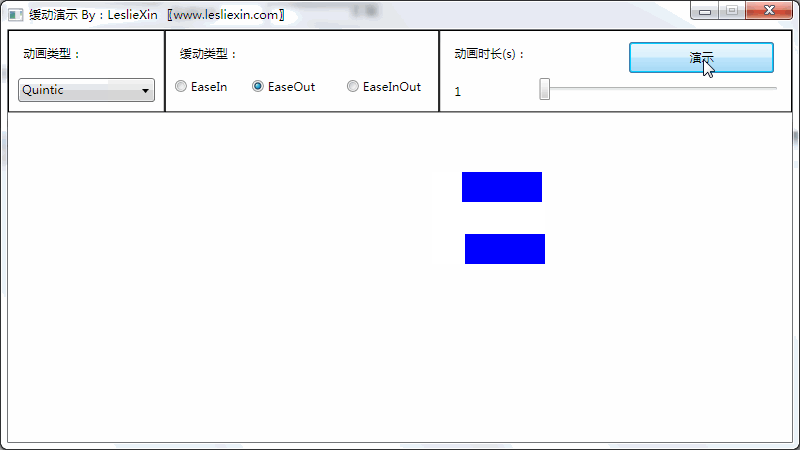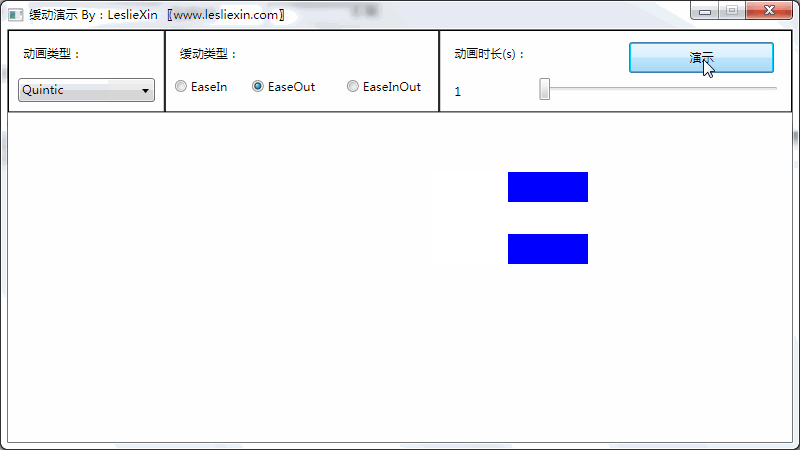
7.3，WPF效果

（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

b，EaseOut：

c，EaseInOut：

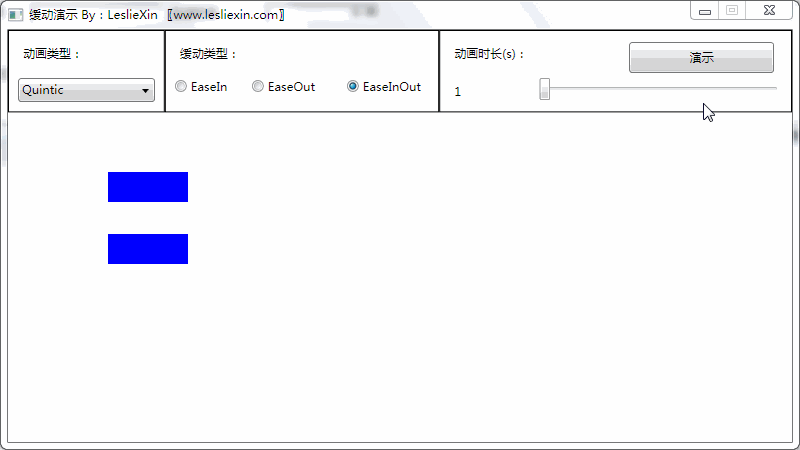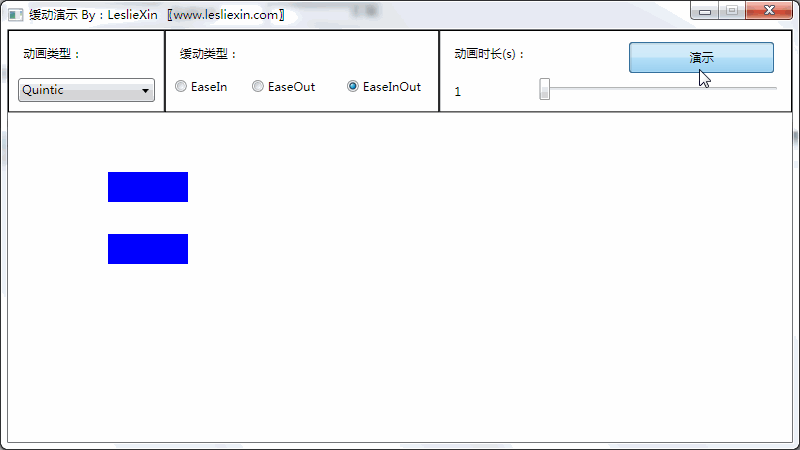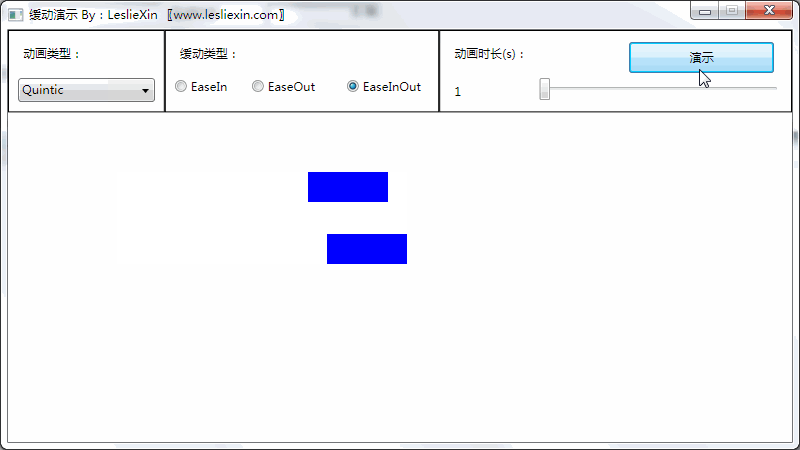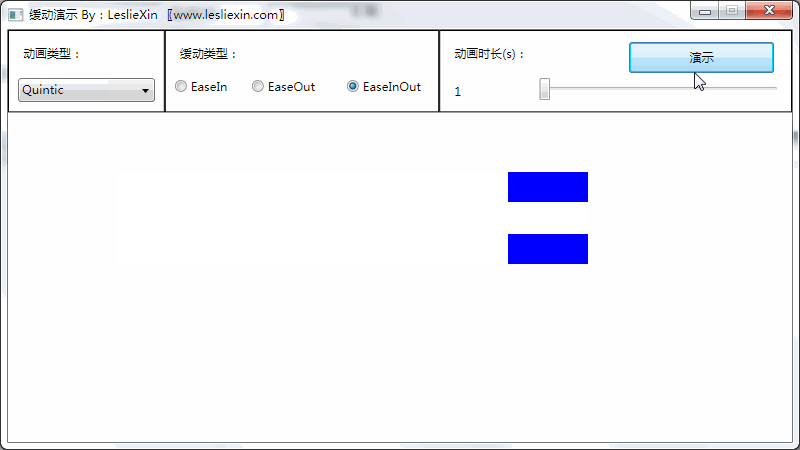
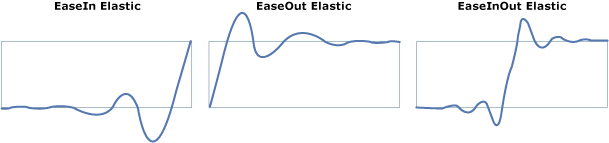
8，Elastic

曲线（图源自MSDN）：

8.1，曲线公式

public static double Elastic(double x, LEaseMode easeMode)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return x == 0 ? 0 : x == 1 ? 1 : -Math.Pow(2, 10 * x - 10) * Math.Sin((x * 10 - 10.75) * 2 * Math.PI / 3);
        case LEaseMode.EaseOut:
            return x == 0 ? 0 : x == 1 ? 1 : Math.Pow(2, -10 * x) * Math.Sin((x * 10 - 0.75) * 2 * Math.PI / 3)+1;
        case LEaseMode.EaseInOut:
            return x == 0 ? 0 : x == 1 ? 1 : x < 0.5 ? -(Math.Pow(2, 20 * x - 10) * Math.Sin((x * 20 - 11.125) * 2 * Math.PI / 4.5)) / 2 : (Math.Pow(2, -20 * x + 10) * Math.Sin((x * 20 - 11.125) * 2 * Math.PI / 4.5)) / 2 + 1;
        default:
            return 0;
    }
}

Elastic

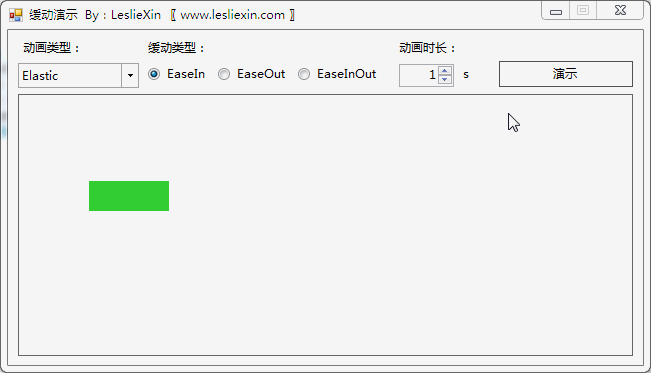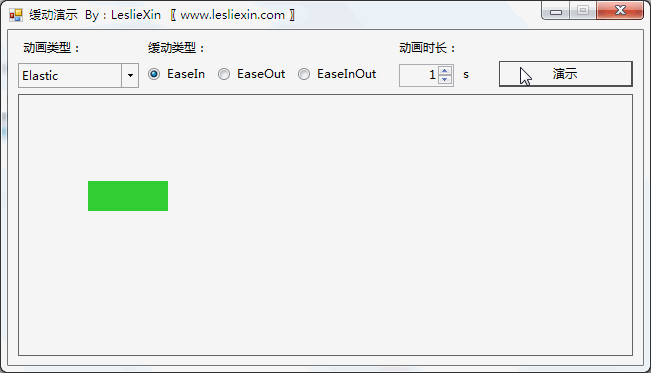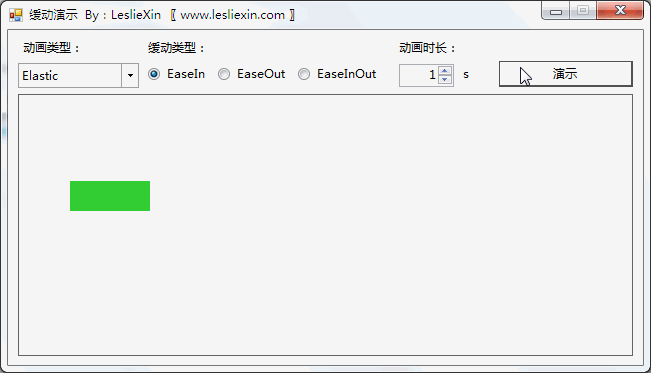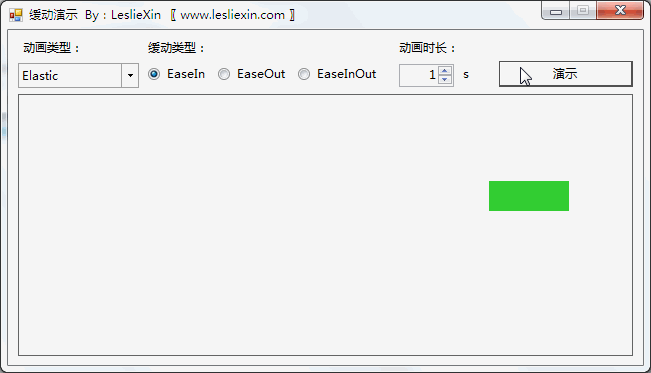
8.2，WinForm效果

a，EaseIn：

b，EaseOut：

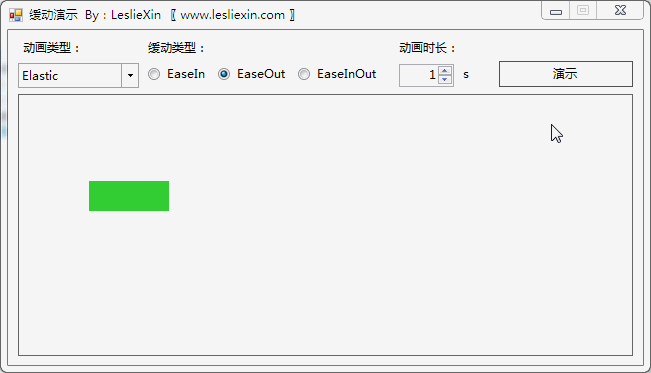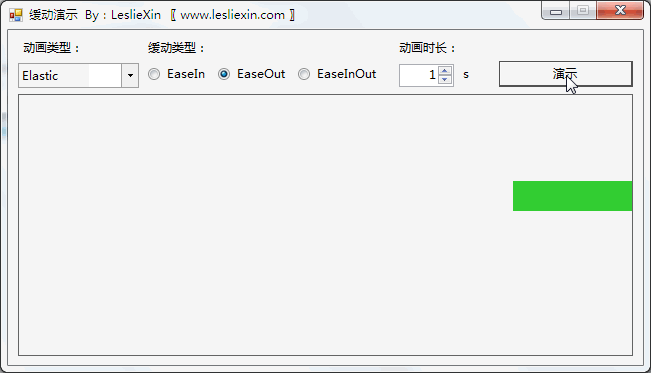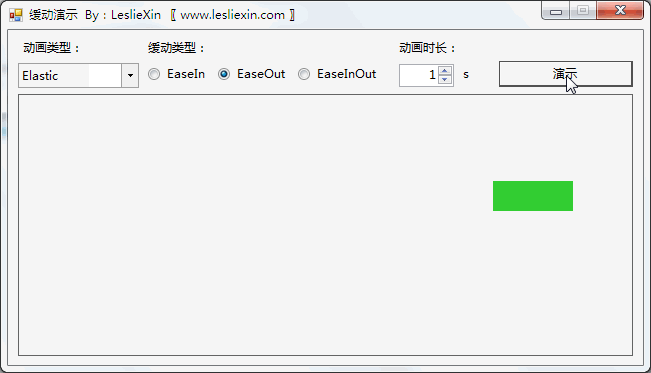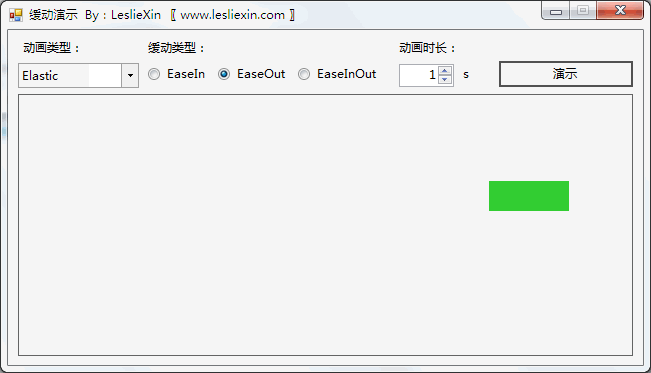
c，EaseInOut：

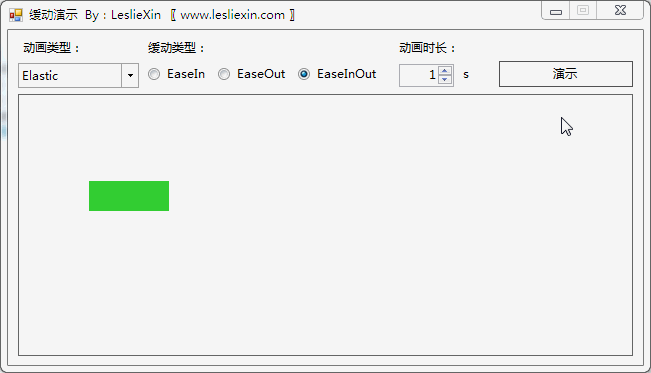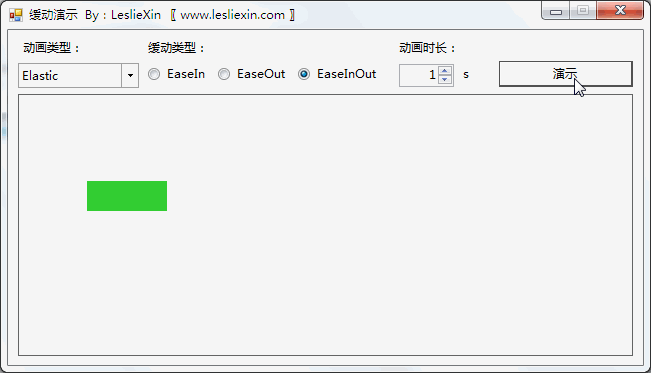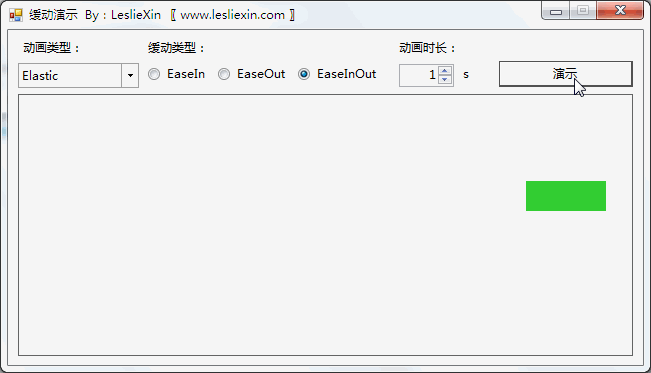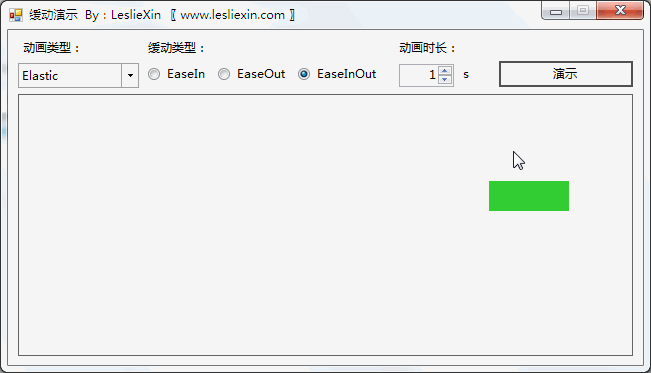
8.3，WPF效果

（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

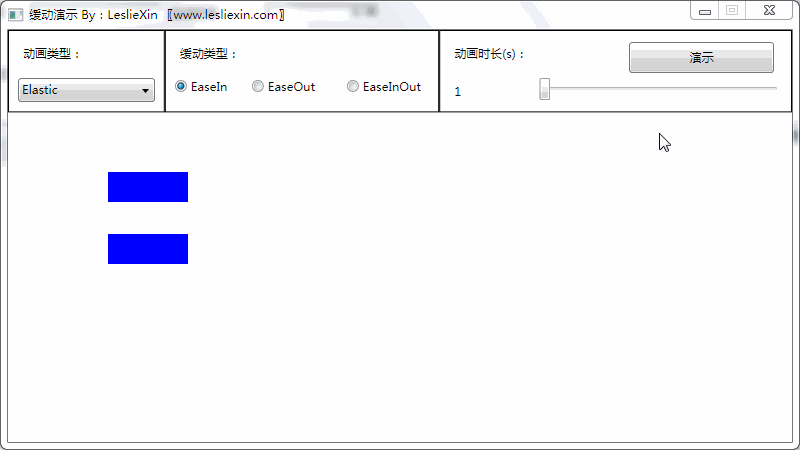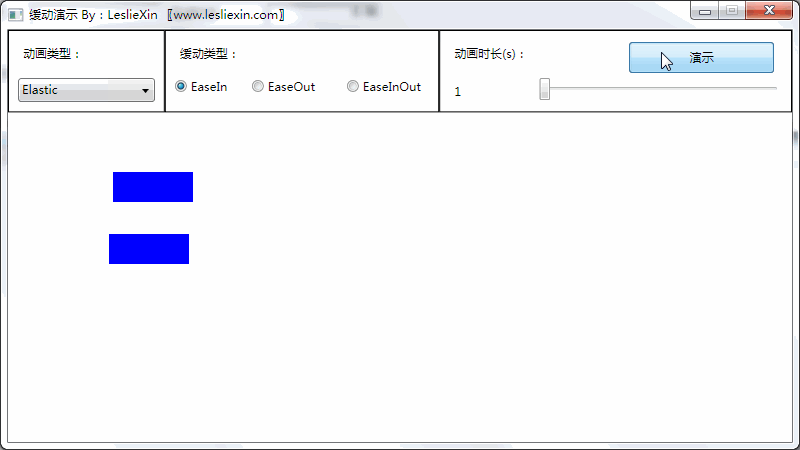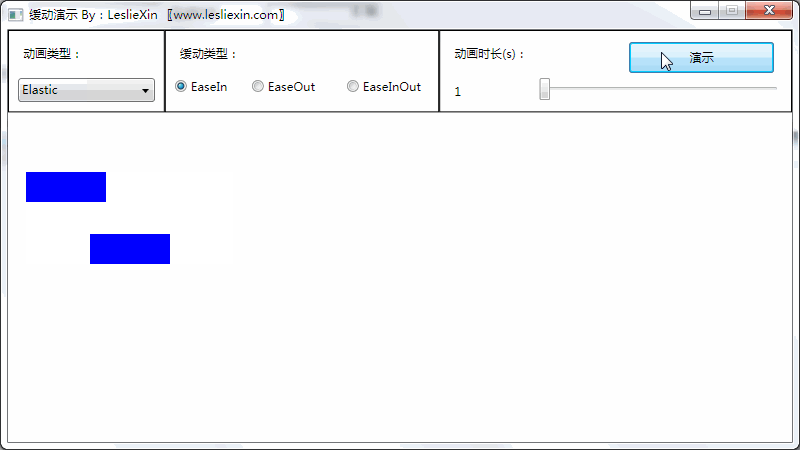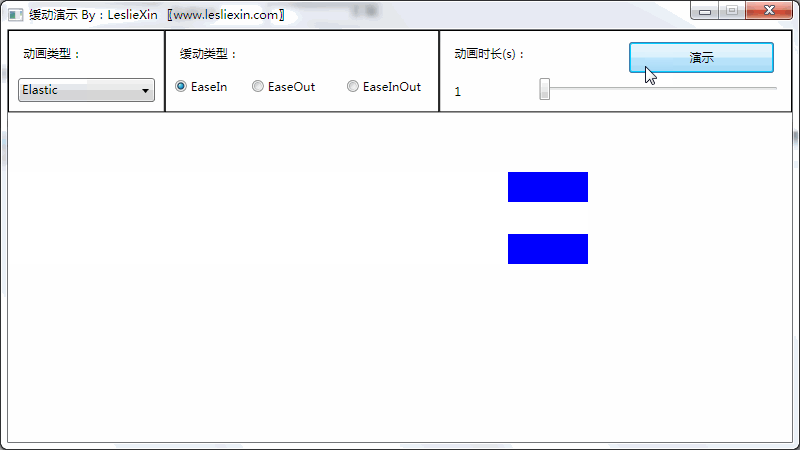
b，EaseOut：

c，EaseInOut：

9，Exponential

曲线（图源自MSDN）：

9.1，曲线公式

public static double Exponential(double x, LEaseMode easeMode)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return x == 0 ? 0 : Math.Pow(2, 10 * x - 10);
        case LEaseMode.EaseOut:
            return x == 1 ? 1 : 1 - Math.Pow(2, -10 * x);
        case LEaseMode.EaseInOut:
            return x == 0 ? 0 : x == 1 ? 1 : x < 0.5 ? Math.Pow(2, 20 * x - 10) / 2 : (2 - Math.Pow(2, -20 * x + 10)) / 2;
        default:
            return 0;
    }
}

Exponential

9.2，WinForm效果

a，EaseIn：

b，EaseOut：

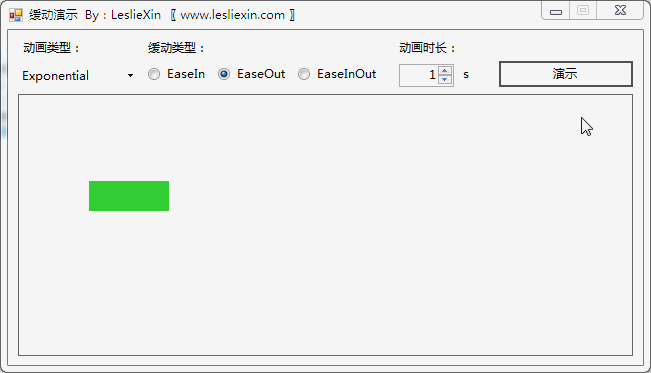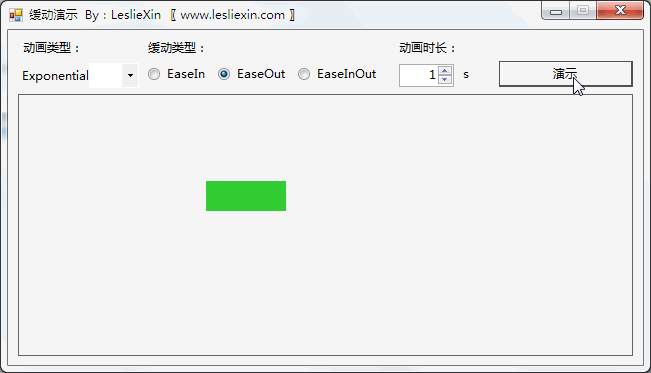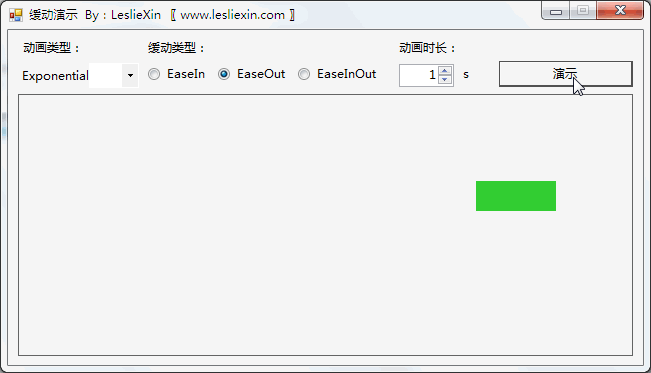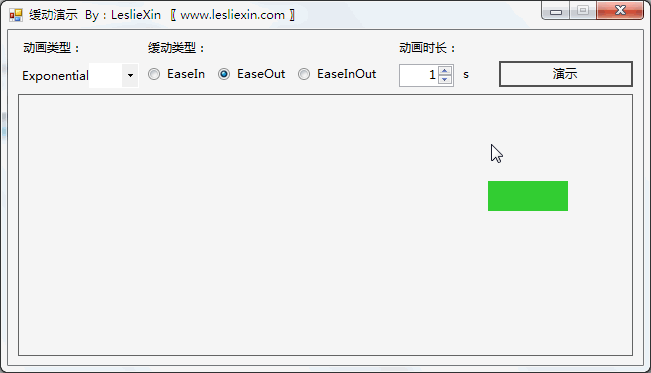
c，EaseInOut：

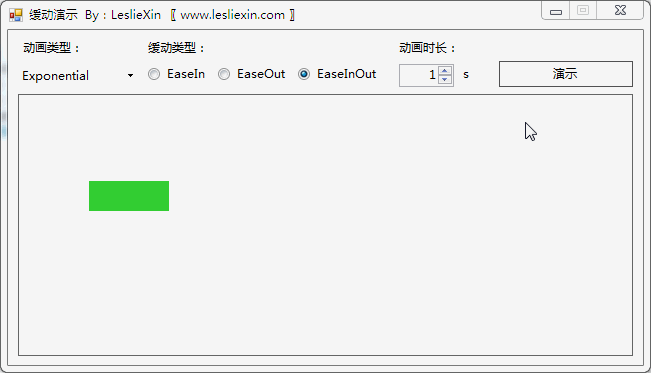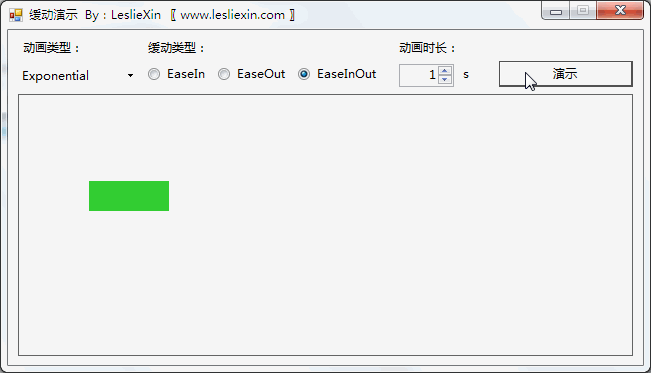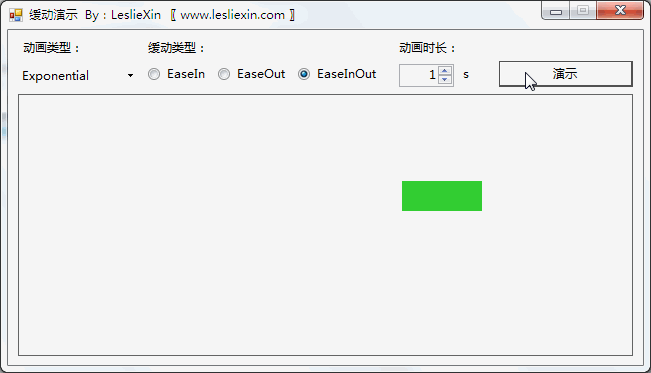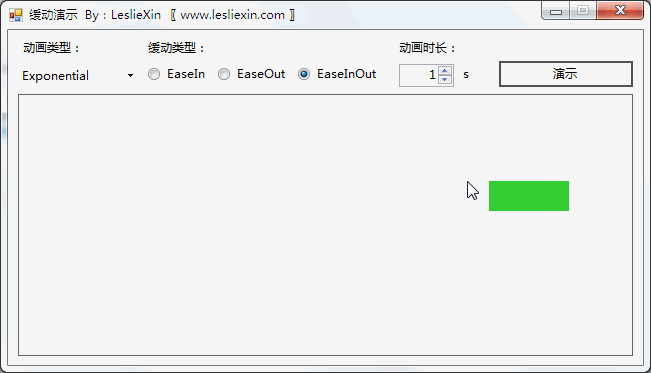
9.3，WPF效果

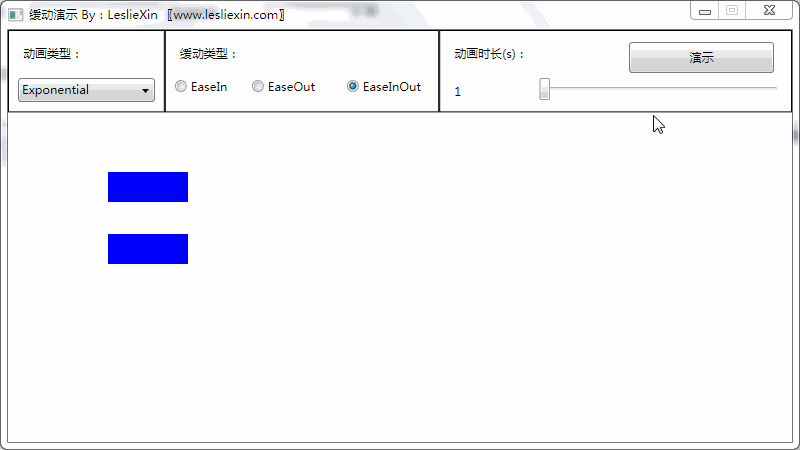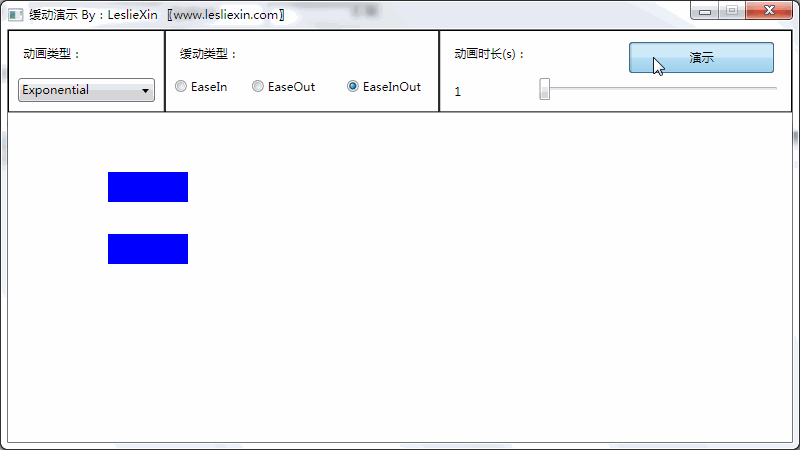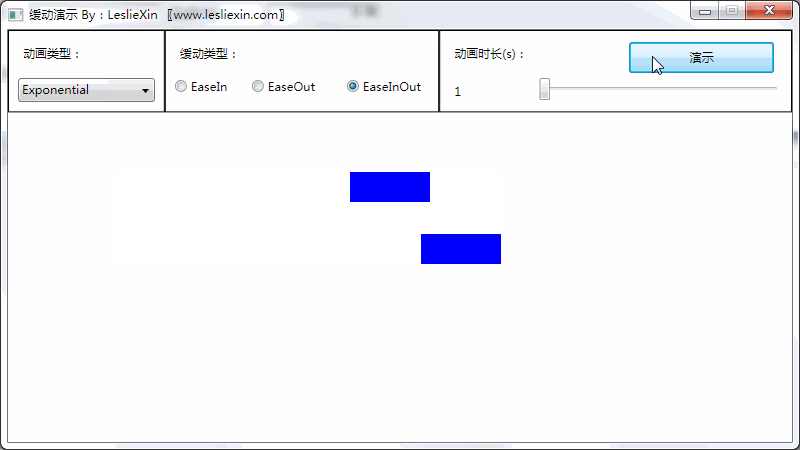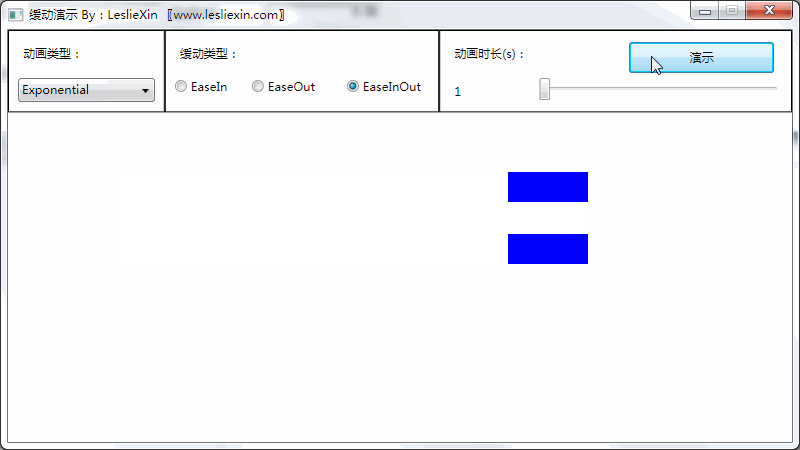
（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

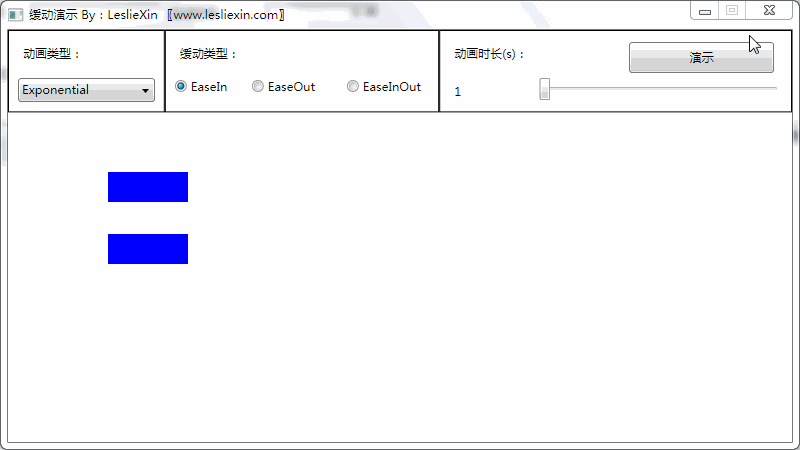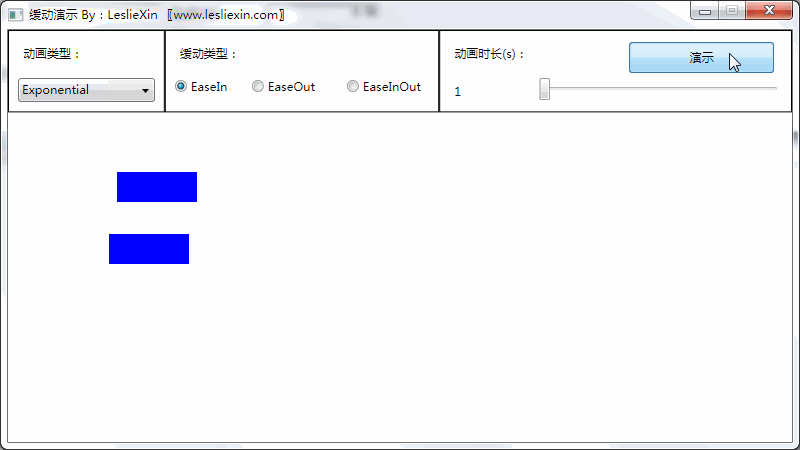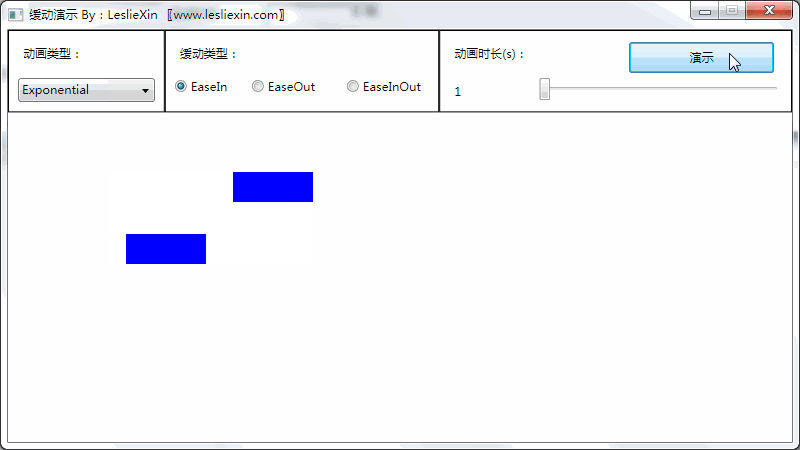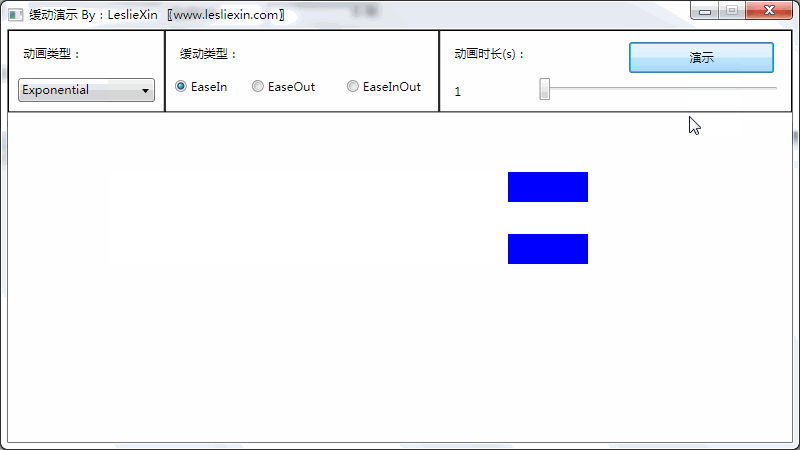
b，EaseOut：

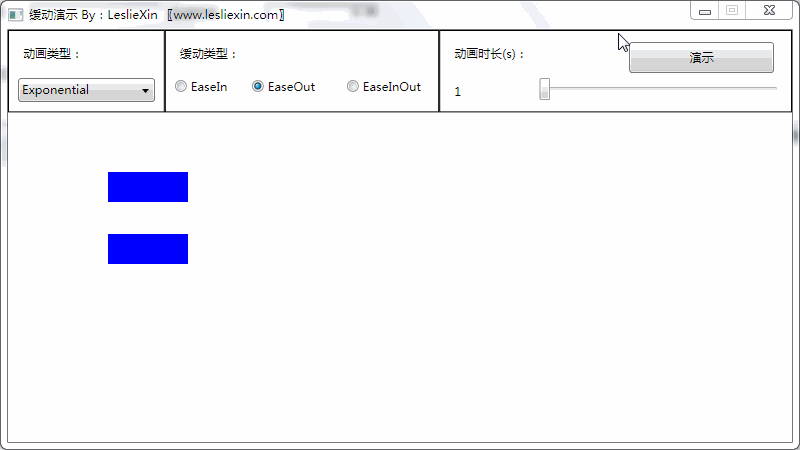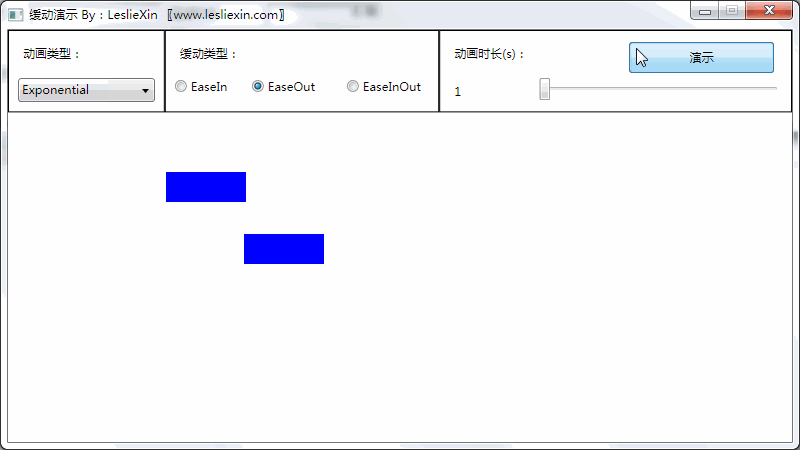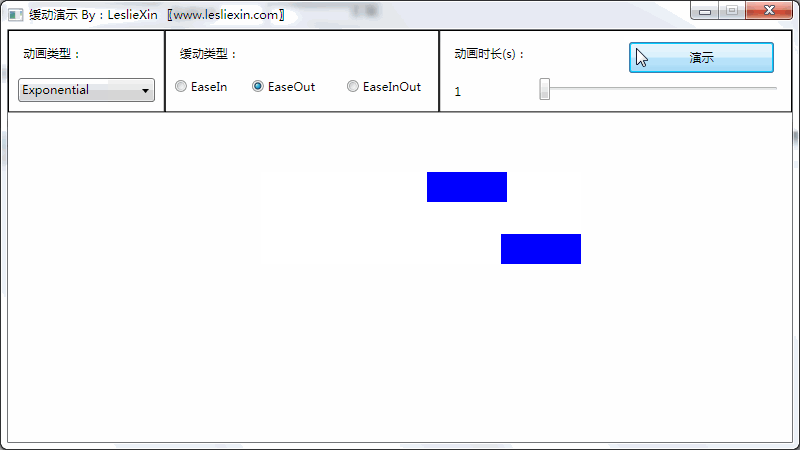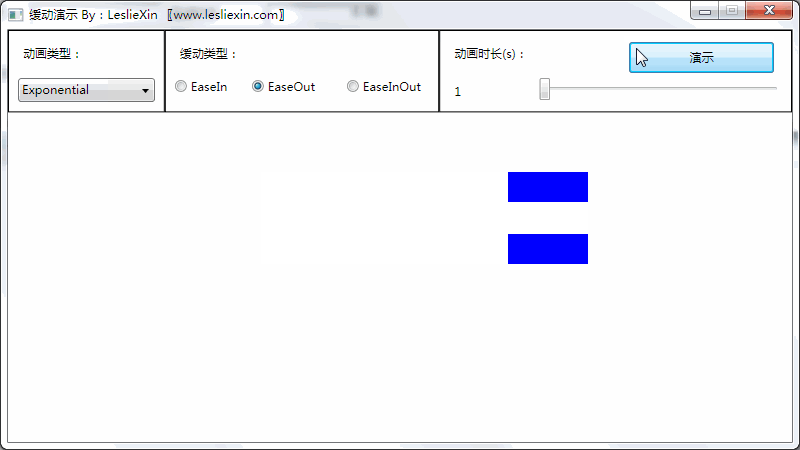
c，EaseInOut：

10，Sine

曲线（图源自MSDN）：

10.1，曲线公式

public static double Sine(double x, LEaseMode easeMode)
{
    switch (easeMode)
    {
        case LEaseMode.EaseIn:
            return 1 - Math.Cos((x * Math.PI) / 2);
        case LEaseMode.EaseOut:
            return Math.Sin((x * Math.PI) / 2);
        case LEaseMode.EaseInOut:
            return -(Math.Cos(Math.PI * x) - 1) / 2;
        default:
            return 0;
    }
}

Sine

10.2，WinForm效果

a，EaseIn：

b，EaseOut：

c，EaseInOut：

10.3，WPF效果

（上面矩形为WPF原版缓动效果，下面矩形为公式实现效果）

a，EaseIn：

b，EaseOut：

c，EaseInOut：

---

四、结束语

通过上面的动图我们会发现，其中一些效果，使用公式生成的与WPF原版的是不一样的，一是因为WPF原版的曲线不是固定的，还有其他参数去调控，而我对比的时候使用的是WPF默认的缓动效果；二是因为一像Bounce、Elastic等曲线以我的能力很难扒出来具体的公式，所以更多的是依照文首的Github上那个项目中的公式。所以难免有所差异。

同时，写本篇文章是因为在之后的自定义控件系列文章，以及其他涉及图形的文章中，会频繁的使用缓动效果以增强直观感受，到时文章中会引用本文所生成的类库，当然也会随文附上缓动公式。

---

五、源代码下载

源代码包含：

1，缓动类库

2，WinForm演示

3，WPF演示

https://files.cnblogs.com/files/lesliexin/LEase.7z