【树形结构】51nod 1766 树上的最远点对

题目内容

\(n\)个点被\(n−1\)条边连接成了一颗树，边有权值\(w_i\)。有\(q\)个询问，给出\([a,b]\)和\([c,d]\)两个区间，表示点的标号请你求出两个区间内各选一点之间的最大距离，即你需要求出

\[\max \{ \text{dis}(i,j)\vert i\in[a,b],j\in [c,d] \}
\]

数据范围

\(1≤n,q≤10^5,1≤w_i≤10^4\)

思路

好像其实是很好写的一道题（虽然考场我写的暴力orz）

先想树的直径的合并性质：

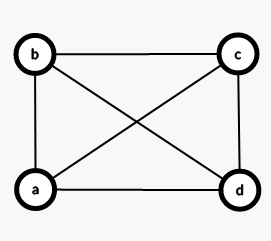
若\(<a,b>\)，\(<c,d>\)分别为原来两棵树的直径，那么合并后的新直径必定为\(<a,b>\)，\(<c,d>\)，\(<a,c>\)，\(<a,d>\)，\(<b,c>\)，\(<b,d>\)中的最大值。

那么对于本题的路径合并也是类似，可以通过反证法证明。

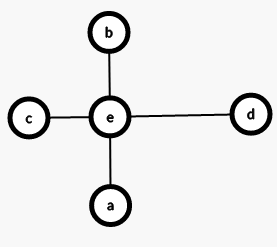
假设原来的直径为\(<a,b>\)，设合并之后的直径不是以\(a,b\)中的为端点而是\(<c,d>\)，那么可以得出\(\text{dis}(b,d)\)和\(\text{dis}(a,d)\)均要小于\(\text{dis}(c,d)\)。可以看出\(<e,d>\)是公共的，那么可以得出\(\text{dis}(b,e)\)和\(\text{dis}(a,e)\)均小于\(\text{dis}(c,e)\)，那么你一开始求直径的时候就会选择\(<b,c>\)或\(<a,c>\)其中一条，而不是\(<a,b>\)。

那么关于这个性质我们就可以开一个线段树，内存最大路径的端点下标，通过以上的性质合并。需要注意的是倍增求\(\text{LCA}\)常数太大会导致超时，所以可以选择树剖或\(\text{ST}\)表求\(\text{LCA}\)。

然后这里提供一种重载运算符的写法，感觉比直接写好多if少很多（但是本人习惯扩行qwq看起来和正常写法差不多），然后本人过于蒻所以不会\(\text{ST}\)表求\(\text{LCA}\)所以写的树剖。

代码

#include <bits/stdc++.h>
#define lson (rt<<1)
#define rson (rt<<1|1)
using namespace std;
const int maxn=1e5+10;
int n,m;

struct Edge{
    int from,to,w,nxt;
}e[maxn<<1];

inline int read(){
    int x=0,fopt=1;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')fopt=-1;
        ch=getchar();
    }
    while(isdigit(ch)){
        x=(x<<3)+(x<<1)+ch-48;
        ch=getchar();
    }
    return x*fopt;
}

int head[maxn],cnt;
inline void add(int u,int v,int w){
    e[++cnt].from=u;
    e[cnt].to=v;
    e[cnt].w=w;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}

int fa[maxn],dep[maxn],siz[maxn],dis[maxn],son[maxn];
void dfs1(int u){
    dep[u]=dep[fa[u]]+1;siz[u]=1;
    for(register int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa[u])continue;
        fa[v]=u;
        dis[v]=dis[u]+e[i].w;
        dfs1(v);
        siz[u]+=siz[v];
        if(!son[u]||siz[v]>siz[son[u]])son[u]=v;
    }
}

int top[maxn];
void dfs2(int u,int t){
    top[u]=t;
    for(register int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa[u])continue;
        dfs2(v,v==son[u]?t:v);
    }
}

inline int lca(int u,int v){
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        u=fa[top[u]];
    }
    return dep[u]<dep[v]?u:v;
}

inline int Getdis(int u,int v){
    return dis[u]+dis[v]-2*dis[lca(u,v)];
}

struct Node{
    int l,r;
    friend inline Node operator +(const Node& A,const Node& B){
        int p[4]={A.l,A.r,B.l,B.r};
        int Max=-1;
        Node res;
        for(int i=0;i<4;i++)
            for(int j=i+1;j<4;j++){
                int w=Getdis(p[i],p[j]);
                if(w>Max){
                    Max=w;
                    res=(Node){p[i],p[j]};
                }
            }
        return res;
    }
}tree[maxn<<2];

inline void pushup(int rt){
    tree[rt]=tree[lson]+tree[rson];
}

inline void Build(int rt,int l,int r){
    if(l==r){
        tree[rt].l=tree[rt].r=l;
        return;
    }
    int mid=(l+r)>>1;
    Build(lson,l,mid);
    Build(rson,mid+1,r);
    pushup(rt);
}

inline Node query(int rt,int l,int r,int s,int t){
    if(s<=l&&t>=r)
        return tree[rt];
    int mid=(l+r)>>1;
    if(t<=mid)return query(lson,l,mid,s,t);
    else if(s>=mid+1)return query(rson,mid+1,r,s,t);
    else return query(lson,l,mid,s,mid)+query(rson,mid+1,r,mid+1,t);
}

inline int Mymax(int a,int b,int c,int d){
    return max(a,max(b,max(c,d)));
}

int main(){
    freopen("D.in","r",stdin);
    freopen("D.out","w",stdout);
    n=read();
    for(register int i=1;i<n;i++){
        int x=read(),y=read(),z=read();
        add(x,y,z);
        add(y,x,z);
    }

    dfs1(1);
    dfs2(1,1);
    Build(1,1,n);

    m=read();
    while(m--){
        int a=read(),b=read(),c=read(),d=read();
        Node x=query(1,1,n,a,b);
        Node y=query(1,1,n,c,d);
        int ans=Mymax(Getdis(x.l,y.l),Getdis(x.l,y.r),Getdis(x.r,y.l),Getdis(x.r,y.r));
        printf("%d\n",ans);
    }
    return 0;
}