poj 3304 Segments（解题报告）

收获：举一反三：刷一道会一道

1：思路转化：（看的kuangbin的思路）

首先是在二维平面中：如果有很多线段能够映射到这个直线上并且至少重合于一点，充要条件： 是过这个点的此条直线的垂线与其他所有直线都相交

取极限情况: 此垂线与直线的交点是端点的情况

则可以通过枚举所有的端点所在的直线进行判断，若不存在这样的直线，则输出No！

细节：枚举的两端点存在重合的情况

为了谨慎起见：枚举所有可能情况，包括输入的线段所在的直线也是垂线的情况

2：直线与线段相交和线段与线段相交的区别：

线段的端点是不可变的，而对于线段所在的直线

bool line_segment(Line l1,Line l2)//l1直线和l2线段相交判断(写反了就会错)
{
    return cmp(det(l2.s,l1.s,l1.e))*cmp(det(l2.e,ll.s,l1.e))<=0;
}

bool segmen_segment(Line l1,Line l2)//线段l1和线段l2
{
    return (cmp(det(l2.s,l1.s,l1.e))*cmp(det(l2.e,l1.s,l1.e))<=0)&&(cmp(det(l1.s,l2.s,l2.e))*cmp(det(l1.e,l2.s,l2.e))<=0);
}

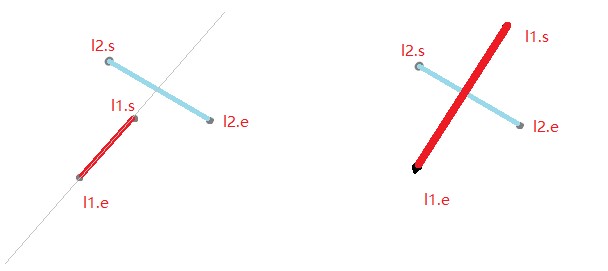
如下图：(此处只讨论严格相交，严格相交：两条线段只有一个公共点，而且这个公共点不是端点)

#include<iostream>
#include<cmath>
//完全参考kuangbin的代码
using namespace std;
const double eps = 1e-8;

int sgn(double x)
{
    if(fabs(x)<eps)return 0;
  if(x<0)return -1;
    return 1;
}

struct Point
{
   double  x,y;
    Point(){};
    Point (double _x,double _y)
     {x=_x;y=_y;}
    Point operator - (const Point &b)const
    {
        return Point(x-b.x,y-b.y);
    }
    double operator *(const Point &b)const
    {
        return x*b.x+y*b.y;
    }
    double operator ^ (const Point &b)const
    {
        return x*b.y-y*b.x;
    }
};

struct Line{
    Point s,e;
    Line() {}
    Line (Point  _s,Point _e)
    {
        s=_s;
        e=_e;
    }
};

const int MAXN=1010;
Line line[MAXN];

double  xmult(Point p0,Point p1,Point p2)//叉积
{
    return (p1-p0)^(p2-p0);
}

bool xmultline(Line l1,Line l2)//判断直线1和线段l2是否相交
{
    //return sgn(xmult(l2.e,l1.e,l1.s))*sgn(xmult(l2.s,l1.e,l1.s))<=0;
    return sgn(xmult (l1.e,l2.e,l2.s))*sgn(xmult(l1.s,l2.e,l2.s))<=0;//错误
}

double dis(Point p1,Point p2)
{
    return sqrt((p1-p2)*(p1-p2));
}
bool check(Line ll,int n)
{
    if(sgn(dis(ll.s,ll.e))==0)return false ;

    for(int i=0;i<n;i++)
    {
        if(xmultline(ll,line[i])==false)
            return false;
    }
    return true;
}

int main ()
{
    int t;
    cin>>t;
    while(t--)
    {
        int m;
        cin>>m;
        double x1,x2,y1,y2;
        for(int i=0;i<m;i++)
        {
            cin>>x1>>y1>>x2>>y2;
            line[i]=Line(Point(x1,y1),Point(x2,y2));
        }
        bool flag= false;
        for(int i=0;i<m;i++)
            for(int j=0;j<m;j++)
            {
                int n=m;
                 if(check(Line(line[i].s,line[j].s),n) || check(Line(line[i].s,line[j].e),n)
                        || check(Line(line[i].e,line[j].s),n) || check(Line(line[i].e,line[j].e),n) )
                   {
                        flag=true;
                        break;
                   }
            }
            if(flag)
                cout<<"Yes!"<<endl;
            else
                cout<<"No!"<<endl;
    }
    return 0;
}

自己照着套路写的：

#include<iostream>
#include<cmath>

using namespace std;

double eps=1e-8;

int cmp(double x)
{
    if(fabs(x)<=eps)return 0;
    if(x<0)return -1;
    return 1;
}

struct Point{
    double x,y;
    Point (){}
    Point (double _x,double _y)
    {
        x=_x,y=_y;
    }
    Point operator -(const Point &b)const
    {
        return Point (x-b.x,y-b.y);
    }
    double operator *(const Point &b)const
    {
        return x*b.x+y*b.y;
    }
    double operator ^(const Point &b)const
    {
        return x*b.y-y*b.x;
    }
    bool operator ==(const Point &b)const//重载==
    {
        if(cmp(fabs(x-b.x))==0&&cmp(fabs(y-b.y)==0))
            return true;
        return false;
    }
};

struct Line{
    Point s,e;
    Line(){}
    Line(Point _s,Point _e)
    {
        s=_s;
        e=_e;
    }
};

const int MAXN =110;
Line line[MAXN];
double xmult(Point p0,Point p1,Point p2)
{
    return (p1-p0)^(p2-p0);
}

bool line_segment(Line l1,Line l2 )//直线l1和线段l2
{
    if(cmp(xmult(l2.s,l1.s,l1.e))*cmp(xmult(l2.e,l1.s,l1.e))<=0)
        return true;
    return false;
}
bool chack(Line ll ,int m)//与所有边相交判断
{
    if(ll.s==ll.e)return false ;
    for(int i=0;i<m;i++)
    {
        if(line_segment(ll,line[i])==false)
            return false;
    }
    return true;
}

int main ()
{
    int t;
    cin>>t;
    int n;
    double x1,x2,y1,y2;
    while(t--)
    {
        cin>>n;
        for(int i=0;i<n;i++)
        {

         cin>>x1>>y1>>x2>>y2;
        line[i]=Line(Point(x1,y1),Point(x2,y2));
        }
        bool flag=false;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
        {
            int m=n;
            if(chack(Line(line[i].s,line[j].s),m)||chack(Line(line[i].s,line[j].e),m)||chack(Line(line[i].e,line[j].s),m)||chack(Line(line[i].e,line[j].e),m))
            flag=true;
        }
        if(flag)
            cout<<"Yes!"<<endl;
        else
            cout<<"No!"<<endl;

    }

    return 0;
}