Numpy_01
# 引子:
# ndarray 是一个 numpy库提供的 同构数据多维模型
import numpy as np
list=[1,2,3,4,5,6]
myndarray=np.array(list)
# type(myndarray) # numpy.ndarray
# myndarray.dtype # dtype('int32')
# print(myndarray) # [1 2 3 4 5 6]
# print(myndarray.shape) # (7,1)
myndarray
# array([1,
# 2,
# 3,
# 4,
# 5,
# 6]) #7行1列数据
array([1, 2, 3, 4, 5, 6])
# numpy的基本用法:
# 一,创建 ndarray:
# 1)np.array()方法: 接收一切序列类型对象,包括其他数组。
# 2)其他方法,如:np.zeros(),np.ones(),np.empty(),np.arange(),np.ones_like(),np.zeros_like(),
# np.eye(),np.empty_like(),np.identity()等。
# 1--ndarray的 基本属性:
import numpy as np
mylist=[1,2,3,4,5]
myarray=np.array(mylist)
print(myarray) # [1 2 3 4 5] 矩阵
print(myarray.ndim) # 1 维数
print(myarray.size) # 5 元素总数
print(myarray.shape) # (5,) 形状 一维数组的形状 (n,)或(1,n)
print(myarray.dtype) # int32 数据类型
print(myarray.itemsize) # 4 每个元素的字节大小 32位/8位(每字节)=4 字节
# 2--特殊的 ndarray:
# 2.1--np.zeros()函数:
np.zeros(5) # array([0., 0., 0., 0., 0.])
np.zeros((2,3))
# 2.2--np.ones()函数:
np.ones(5) # array([1., 1., 1., 1., 1.])
np.ones((2,3))
# 2.3--np.empty()函数:
# empty函数可以创建一个没有具体值的数组(即垃圾值):
np.empty((2,2)) # 认为np.empty返回全0数组是不安全的,很多情况下,返回的都是一些未初始化的垃圾值,比如:
# array([[1.14800323e-311, 6.95177601e-310],
# [6.95177601e-310, 1.14898595e-311]])
# 2.5--np.ones_like()函数和np.zeros_like()函数:
arr01=np.array([[1,2,3,4],[5,6,7,8]])
arro1
# array([[1, 2, 3, 4],
# [5, 6, 7, 8]])
arr02=np.zeros_like(arr01)
arr02
# array([[0, 0, 0, 0],
# [0, 0, 0, 0]])
arr03=np.ones_like(arr01)
arr03
# array([[1, 1, 1, 1],
# [1, 1, 1, 1]])
arr04=np.array([["a",1,"s"],["c",2,"v"]])
arr04
# array([['a', '1', 's'],
# ['c', '2', 'v']], dtype='<U1')
arr05=np.ones_like(arr04)
arr05
# array([['1', '1', '1'],
# ['1', '1', '1']], dtype='<U1')
# 2.6--np.arange()函数:模仿指定的ndarray创建全1或全0数组。
# arange函数类似于python的内置函数range,但arange函数主要用于创建数组。
np.arange(5) # array([0, 1, 2, 3, 4])
np.arange(1,5) # array([ 1, 2, 3, 4])
np.arange(1,10,2) # array([1, 3, 5, 7, 9])
# 2.7--np.eye()函数,np.empty_like()函数,np.identity()函数, np.asarray()函数:
# 用到再来学习。
# 二,ndarray 的数据类型
# Numpy既可以为新建的数组【推断】出合适的数据类型,也可以通过【dtype属性来指定类型】。
# Numpy有很多数据类型,记住下面这些常用的就可以:
# folat int complex复数 bool布尔 string_ python对象:object
# 各数据类型及代码以及数据类型的解释见《利用python及逆行数据分析(2)》p121
# 1--数据类型推断:
arr01=np.array([0,1,2,3,4])
arr01.dtype # dtype('int32')
# 2--为数组指定数据类型时:
arr01=np.array([0,1,2,3,4],dtype='float64')
arr01.dtype # dtype('folat64')
arr02=np.arange(10,dtype='float')
arr02.dtype # dtype('float64')
# 3--使用astype显示转换数据类型,不改变原数组,返回一个新数组:
# 语法:newarr=arr.astype([np.]数据类型)方法 或 newarr=arr.astype(arr2.dtype)方法 使用其他数组的dtype作为参数。
# 3-1)将数值型转为字符串:
arr01=np.array([0,1,2,3,4],dtype='float64')
arr02=arr01.astype(np.string_)
arr01.dtype # dtype('float64')
arr02.dtype # dtype('S32')
# 3-2)将浮点型数组转为整数,并不会四舍五入,而是直接截断
arr01=np.array([0,1,2.5,3.1,4.2],dtype='float64')
arr02=arr01.astype(np.int32)
arr02.dtype #dtype('int32')
arr02 # array([0, 1, 2, 3, 4])
# 3-3)将字符串型的数字的数组转成数值类型:
arr01=np.array(['0','1','2.5','3.1','4.2'])
arr02=arr01.astype(np.float64)
arr02 # array([0. , 1. , 2.5, 3.1, 4.2])
arr02.dtype # dtype('float64')
# 如果数组里有字符型字符串,使用astype转为数值就会报错:
arr01=np.array(['a','1','e','3.1','4.2'])
arr02=arr01.astype(np.float64) #ValueError: could not convert string to float: 'a'
arr02
# 3-4)使用其他数组的数据类型 newarr=arr.astype(arr2.dtype)方法
arr01=np.array([0,1,2,3,4],dtype='float64')
arr02=np.array(["1","4","5"])
arr03=arr02.astype(arr01.dtype)
arr03.dtype
# 三,数组和标量之间的运算 (+ - * / **)
# 数组之所以很重要,是因为它不需要编写循环就可以对数组内每一个数据元素进行运算,通常称之为矢量化。
# -- 不同大小的数组之间的运算叫做广播,这里不对广播机制做深入了解。
# -- 大小相等的数组之间的任何算术运算都会将运算应用到元素级:
# 1--数组准备
arr=np.array([[1.,2.,3.],[4.,5.,6.]]) # 或 arr=np.arange(1.0,7.0).reshape(2,3)
arr
# array([[1., 2., 3.],
# [4., 5., 6.]])
# 2--数组与数组:
# 2-1)数组×数组
arr*arr
# array([[ 1., 4., 9.],
# [16., 25., 36.]])
# 2-2)数组-数组
arr-arr
# array([[0., 0., 0.],
# [0., 0., 0.]])
# 3--数组与标量:
1/arr
# array([[1. , 0.5 , 0.33333333],
# [0.25 , 0.2 , 0.16666667]])
arr**2
# array([[ 1., 4., 9.],
# [16., 25., 36.]])
arr-0.5
# array([[0.5, 1.5, 2.5],
# [3.5, 4.5, 5.5]])
# 4--数组与标量的混合运算
3*arr+2
# array([[ 5., 8., 11.],
# [14., 17., 20.]])
# 5--数组元素比较, 返回布尔值类型数组
arr2 = np.array([[0., 4., 1.], [7., 2., 12.]])
arr>arr2
# array([[ True, False, True],
# [False, True, False]])
# 四,基本索引和切片
# Numpy 数组的索引方法非常多。
# 1 一维数组的元素索引和数组切片:
# 1)一维数组元素的访问:
arr=np.arange(10)
arr[5] # 5
# 2)一维数组的切片:
arr[5:8]
array([5, 6, 7])
# 3)一维数组切片赋值:
# 会影响原数组(数组的切片是原数组的视图,这和python的list切片是原list的浅复制不同)之所以会这样,是因为Numpy是为大数据考虑的,
# 如果不是在原数组上操作,而是复制来复制去,会非常占用内存。
arr[3:7]=0 # 或: arr_slice=arr[3:7] arr_slice=0
arr # array([ 0, 1, 2, 0, 0, 0, 0, 7, 8, 9])
arr_slice2=arr[6:9]
arr_slice2[0]=9999 # 改变切片的第一个元素值
arr_slice2[1:]=8888
arr # array([ 0, 1, 2, 0, 0, 0, 9999, 8888, 8888, 9])
# 4)一维数组切片的显式复制(浅复制):
# 语法:arr[5:8].copy()
arr=np.arange(10)
arr2=arr[5:8].copy()
arr2[:]=777
arr2 # array([777, 777, 777])
arr # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) 原数组没变
# 2 高维(二维)数组元素的索引和切片: 三维数组暂时不需要考虑
# 1) 创建一个二维数组 (3,3)
arr2d=np.arange(1,10).reshape(3,3)
arr2d
# array([[1, 2, 3],
# [4, 5, 6],
# [7, 8, 9]])
# 1-1)二维数组的元素索引:
arr2d[2]
array([7, 8, 9])
arr2d[2][1] # 或
arr2d[2,1] 8
# 1-2)二维数组的切片:
arr2d[:2] # 沿着0轴选取元素
# array([[1, 2, 3],
# [4, 5, 6]])
arr2d[:2].shape #
# (2,3) 二维数组
arr2d[:2,1:]
# array([[2, 3],
# [5, 6]])
arr2d[:2,1:].shape
# (2,2)
arr2d[:,1]
# array([2, 5, 8])
arr2d[:,1].shape
# (3,) 一维数组
arr2d[:,:1]
array([[1],
[4],
[7]])
arr2d[:,:1].shape
#(3, 1) 二维数组
#当然,对切片的赋值也会影响到原数组:
arr2d[:,:1]=9
arr2d
array([[9, 2, 3],
[9, 5, 6],
[9, 8, 9]])
# 五,布尔索引
# 示例:
# 数组1:一个用于存储数据的数组以及一个存储姓名的数组(含有重复项)。
# 数组2:使用np.random中的 randn函数生成一些正态分布的随机数据。
# 1)生成数组1 names :
names=np.array(["Bob","Joe","Will","Bob","Will","joe","joe"])
names # array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'joe', 'joe'], dtype='<U4')
# 2) 生成 数组2 data:
data=np.random.randn(7,4)
data
array([[ 0.13914193, -0.96275352, 0.35075216, 0.25364798],
[-1.10364635, -0.2635838 , -0.84638153, 0.67202326],
[-0.83869909, -0.06954938, 0.80021281, -2.44477926],
[-0.08734994, -0.08249876, 0.07469813, 0.27376429],
[ 1.0876769 , 1.45565495, -2.602985 , -0.89583722],
[-0.24046131, 0.68823067, -0.34271733, -1.67964804],
[ 0.12394175, 2.32313088, 0.23627141, 1.7670217 ]])
# 1--获取一个布尔数组,并使用布尔数组获取另一个数组的数组切片:
# 1)等号==的使用
# 假设names 中每一个名字都对应 data中的每行数据,现在我们要选出对应于‘Bob’的每一行数据。
bool_Bob = names == 'Bob' # names == 'Bob' 返回一个布尔类型的数组, ==在数组中也是矢量化的。
bool_Bob
# array([ True, False, False, True, False, False, False])
# np.array([ True, False, False, True, False, False, False]).shape # (7,)
# data.shape # (7,4)
# 将这个布尔数组作为 data 数组的索引: #【布尔型数组的长度】必须和【被索引的轴】长度一致。
data[names == 'Bob'] # 相当于:data[ True, False, False, True, False, False, False] 或 data[bool_Bob]
array([[ 0.13914193, -0.96275352, 0.35075216, 0.25364798], [-0.08734994, -0.08249876, 0.07469813, 0.27376429]])
# 还可以将布尔型数组与切片,整数(或整数序列)混合使用:
data[names=='Bob',2:] # 与切片混合使用,第3列及以后列
array([[ 0.20745417, 1.59998866],
[-1.54179944, 0.26520684]])
data[names=='Bob',3] # 与整数混合使用,第4列
array([0.59981237, 2.19444112])
# 2)不等号!=的使用:
data[names!='Bob']
array([[-1.52854216, 0.25771145, -1.23529507, 0.18793414],
[-0.16193399, -0.51354289, 1.90586211, -0.58838872],
[ 0.47066932, 1.69033558, -0.47329781, -0.01530668],
[ 1.23895961, -1.91537102, -1.50733678, 0.16473193],
[-0.59033351, 0.36576441, 2.36265923, -1.1060814 ]])
# 3) ~和==的联用,效果同 !=:
data[~(names=='Bob')]
array([[-1.52854216, 0.25771145, -1.23529507, 0.18793414],
[-0.16193399, -0.51354289, 1.90586211, -0.58838872],
[ 0.47066932, 1.69033558, -0.47329781, -0.01530668],
[ 1.23895961, -1.91537102, -1.50733678, 0.16473193],
[-0.59033351, 0.36576441, 2.36265923, -1.1060814 ]])
# 4)逻辑或 |的使用(别忘了使用()): python中的 or 在数组里是无效的
mask=(names=='Bob')|(names=='Will')
mask
array([ True, False, True, True, True, False, False])
data[mask]
array([[ 0.9965483 , -0.88256842, -0.12551621, 0.59981237],
[-0.16193399, -0.51354289, 1.90586211, -0.58838872],
[ 0.28340236, -0.93341777, -0.48931644, 2.19444112],
[ 0.47066932, 1.69033558, -0.47329781, -0.01530668]])
# 5)逻辑与 & 的使用: python中的 and 在数组中是无效的
mask=(names=='Bob')&(names=='Will')
# names中元素的值是确定的,不可能既是‘Bob’又是的'Will',所以可以预想 mask 的元素全是False
mask
data[mask] # 空数组
array([], shape=(0, 4), dtype=float64)
# 2--通过布尔型索引来选取数组中所有符合条件的元素数据,并改变这些元素的值:
data[data<0]
array([-0.96275352, -1.10364635, -0.2635838 , -0.84638153, -0.83869909,
-0.06954938, -2.44477926, -0.08734994, -0.08249876, -2.602985 ,
-0.89583722, -0.24046131, -0.34271733, -1.67964804]) # 它的 shape是(14,) 一维数组
data[data<0]=0 # 对切片进行赋值
data # 从而改变原数组:
array([[0.13914193, 0. , 0.35075216, 0.25364798],
[0. , 0. , 0. , 0.67202326],
[0. , 0. , 0.80021281, 0. ],
[0. , 0. , 0.07469813, 0.27376429],
[1.0876769 , 1.45565495, 0. , 0. ],
[0. , 0.68823067, 0. , 0. ],
[0.12394175, 2.32313088, 0.23627141, 1.7670217 ]])
data[data==0]=0.1
data
array([[0.13914193, 0.1 , 0.35075216, 0.25364798],
[0.1 , 0.1 , 0.1 , 0.67202326],
[0.1 , 0.1 , 0.80021281, 0.1 ],
[0.1 , 0.1 , 0.07469813, 0.27376429],
[1.0876769 , 1.45565495, 0.1 , 0.1 ],
[0.1 , 0.68823067, 0.1 , 0.1 ],
[0.12394175, 2.32313088, 0.23627141, 1.7670217 ]])
data[(data==0.1)|(data<0.2)]=0.25 # 别忘了加()
data
array([[0.25 , 0.25 , 0.35075216, 0.25364798],
[0.25 , 0.25 , 0.25 , 0.67202326],
[0.25 , 0.25 , 0.80021281, 0.25 ],
[0.25 , 0.25 , 0.25 , 0.27376429],
[1.0876769 , 1.45565495, 0.25 , 0.25 ],
[0.25 , 0.68823067, 0.25 , 0.25 ],
[0.25 , 2.32313088, 0.23627141, 1.7670217 ]])
# 3--通过布尔型索引来选取数组中所有符合条件的行或列数据,并改变这些行或列的值:
# 1)为整行赋值:
data[names=='joe']=7
data
array([[0.25 , 0.25 , 0.35075216, 0.25364798],
[0.25 , 0.25 , 0.25 , 0.67202326],
[0.25 , 0.25 , 0.80021281, 0.25 ],
[0.25 , 0.25 , 0.25 , 0.27376429],
[1.0876769 , 1.45565495, 0.25 , 0.25 ],
[7. , 7. , 7. , 7. ],
[7. , 7. , 7. , 7. ]])
# 2)为整列赋值:
bool_arr=np.array([False,False,True,False])
data=data.swapaxes(0,1) # 先把 data 数组轴对换返回的是一个新的数组赋值给 data。
data[bool_arr]=100 # 为新数组data的行赋值,相当于为旧数组的列赋值。
data=data.swapaxes(0,1) # 将 data再次转回来。
data
array([[ 0.25 , 0.25 , 100. , 0.25364798],
[ 0.25 , 0.25 , 100. , 0.67202326],
[ 0.25 , 0.25 , 100. , 0.25 ],
[ 0.25 , 0.25 , 100. , 0.27376429],
[ 1.0876769 , 1.45565495, 100. , 0.25 ],
[ 7. , 7. , 100. , 7. ],
[ 7. , 7. , 100. , 7. ]])
# 六,花式索引(整数数组索引)
# 与切片的一个很大不同点是,它总是将数据复制到新数组中,对花式索引结果的赋值,不影响原数组,因为其形状与原数组都不一样了,
# 自然没法赋值给原数组。
# 1) 首先准备一个8x4的数组:
arr84=np.empty((8,4))
for i in range(8):
arr84[i]=i # 为每一行赋一个值
arr84
array([[0., 0., 0., 0.],
[1., 1., 1., 1.],
[2., 2., 2., 2.],
[3., 3., 3., 3.],
[4., 4., 4., 4.],
[5., 5., 5., 5.],
[6., 6., 6., 6.],
[7., 7., 7., 7.]])
# 2) 使用指定顺序的【整数列表】或【ndarray】作为索引来选取特定顺序的子集:
# 2-1)使用一个整数【列表】作为索引 (注意索引为列表,如果少了[]就会报错: IndexError: too many indices for array)
arr84[[4,3,0,6]] # 取arr84数组的第5,第4,第1和第7行数据
array([[4., 4., 4., 4.],
[3., 3., 3., 3.],
[0., 0., 0., 0.],
[6., 6., 6., 6.]])
arr84[[-3,-5,-7]] #使用负的索引,会从数组的末尾开始选行,-3表示倒数第三行。
array([[5., 5., 5., 5.],
[3., 3., 3., 3.],
[1., 1., 1., 1.]])
# 2-2)使用多个整数列表作为索引: 返回一维数组
# 分别从各个整数列表里各自选出对应元素组成位置元组 进行索引后组成一维数组
# 1)先准备一个数组:
newarr84=np.arange(32).reshape((8,4))
newarr84
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23],
[24, 25, 26, 27],
[28, 29, 30, 31]])
# 2)对于二维数组的花式索引最多可以使用两个整数列表:
# 对于二维数组,最多可用两个整数列表,列表的长度可不定,但两个列表的长度要保持一致,
# 第一个列表的【每个整数值】不能超过 0轴(行,第1维)的长度,第二个列表的【每个整数值】不能超过 1轴(列,第二维)的长度。
newarr84[[1,5,7,2],[0,3,1,2]] # array([4,23,29,10])
newarr84[[1,5,7,2,5],[0,3,1,2,1]] # array([4,23,29,10,21])
# 3)如果你想得到的不是一维数组,而是一个包含上述元素且按照上述元素出现顺序的矩形区域,那么可以使用下面两种方法:
# 此矩形区域的行数和列数都可以和原数组不同。
# 3-1):
newarr84[[1,5,7,2]][:,[0,3,1,2]] # 4x4 分开写:new=newarr84[[1,5,7,2]],new2=new[:,[0,3,1,2]] 输出new2
# 另一种写法:newarr84[np.ix_([1,5,7,2],[0,3,1,2])]
array([[ 4, 7, 5, 6],
[20, 23, 21, 22],
[28, 31, 29, 30],
[ 8, 11, 9, 10]])
newarr84[[1,5,7,2,5]][:,[0,3,1,2,1]] # 5x5 分开写:new=newarr84[[1,5,7,2,5]],new2=new[:,[0,3,1,2,1]] 输出new2
# 另一种写法:newarr84[np.ix_([1,5,7,2,5],[0,3,1,2,1])]
array([[ 4, 7, 5, 6, 5],
[20, 23, 21, 22, 21],
[28, 31, 29, 30, 29],
[ 8, 11, 9, 10, 9],
[20, 23, 21, 22, 21]])
# 对花式索引的结果赋值,不影响原来的数组。
newarr84[np.ix_([1,5,7,2],[0,3,1,2])]=0
newarr84[np.ix_([1,5,7,2],[0,3,1,2])]
array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]])
newarr84
array([[ 0, 1, 2, 3],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[12, 13, 14, 15],
[16, 17, 18, 19],
[ 0, 0, 0, 0],
[24, 25, 26, 27],
[ 0, 0, 0, 0]])
# 七,数组转置和轴对换
# 转置是重塑的一种特殊形式,返回的是原数组的视图(不会进行任何复制操作)
# arr和arr.T ,arr.transpose() 都是arr的不同形式,对arr.T ,arr.transpose(),array.swapaxes()的赋值操作都会影响arr
# 1)array.T 属性 2)array.transpose()方法 3)array.swapaxes()方法
# 对于二维数组:
arr35=np.arange(15).reshape((3,5))
arr35
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
# 1)array.T 属性:
arr35.T
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])
arr35 # arr35还是arr35
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
arr35.T[1]=-1 # 对转置后的第二行进行赋值:
arr35.T
array([[ 0, 5, 10],
[-1, -1, -1],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])
arr35
array([[ 0, -1, 2, 3, 4],
[ 5, -1, 7, 8, 9],
[10, -1, 12, 13, 14]])
# 来做个计算矩阵内积的示例:np.dot 即矩阵的点乘
arr35=np.arange(15).reshape((3,5))
arrdot=np.dot(arr35.T,arr35)
arrdot
array([[125, 140, 155, 170, 185],
[140, 158, 176, 194, 212],
[155, 176, 197, 218, 239],
[170, 194, 218, 242, 266],
[185, 212, 239, 266, 293]])
# 2) arr.transpose(轴号元组)
# 对于二维数组:
arr35=np.arange(15).reshape((3,5))
arr35.transpose((1,0))
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])
arr35
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
arr35=np.arange(15).reshape((3,5))
arr35.transpose((1,0))[0]=-6
arr35
array([[-6, 1, 2, 3, 4],
[-6, 6, 7, 8, 9],
[-6, 11, 12, 13, 14]])
# 3)array.swapaxes(一对要对换的轴编号)方法, 参数是两个轴号,不是元组。
arr35=np.arange(15).reshape((3,5))
arr35.swapaxes(0,1) # 也可 arr35.swapaxes(1,0)
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])
arr35
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
arr35.swapaxes(0,1)[0]=-2
arr35
array([[-2, 1, 2, 3, 4],
[-2, 6, 7, 8, 9],
[-2, 11, 12, 13, 14]])
arr35
# 八,通用函数 ufunc:快速的元素级的数组函数
# 可以看作是简单函数(接受一个或多个标量值,并产生一个或多个标量值)的矢量化包装器。
# 许多ufunc都是简单的元素级变体,如sqrt,exp:
# 一元 ufunc:
# abs,fabs--计算整数,浮点数,复数的绝对值,对于非复数值,可以使用更快的fabs
# sqrt------计算各元素的平方根,相当于arr**0.5
# square----计算各元素的平方,相当于arr**2
# exp-------计算各元素的以e为底的指数
# log,log10,log2,log1p--分别表示自然对数,底数为10的log,底数为2的log,log(1+x)
# sign--计算各元素的正负号:1(正数),0(零),-1(负数)
# ceil--计算各元素的ceiling值,即大于等于该值的最小整数。 (天花板值)
# floor--计算该值的floor值,即小于等于该值的最大整数。(地板值)
# rint--将各元素的值四舍五入到最接近的整数,保留dtype。
# modf--将数组的小数和整数部分以两个独立数组的形式返回。
# isnan--返回一个表示哪些值是 NAN (not a number)的布尔型数组
# isfinite--返回一个表示哪些元素是有尽的(非inf,非NAN)的布尔型数组
# isinf--返回一个表示哪些元素是无穷的的布尔型数组
# cos,cosh,sin,sinh,tan,tanh--普通型和双曲型三角函数
# arccos,aeccosh,arcsin,arcsinh,arctan,arctanh--反三角函数
# logicl-not--计算各元素not x的真值。相当于 -arr
# 二元ufunc:
# add--将两个数组中对应的元素相加
# subtract--将两个数组中对应的元素相减
# multiply--将两个数组中对应的元素相乘
# devide,floor_divide--除法或向下圆整除法(丢弃余数)
# power--对于第一个数组中的元素A,根据第二个数组中的相应的元素B,计算A**B
# maximum,fmax--元素级的最大值计算,fmax将忽略NAN
# minimum,fmin--元素级的最小值计算,fmin将忽略NAN
# mod--元素级的取模计算(除法的余数)余数。
# copysign--将第二个数组中的符号复制给第一个数组中的值
# greater、greater_equal、less、less_equal、equal、not equal--执行数组元素的比较运算,产生布尔型数组。相当于中辍运算符 >,>=,<,<=,==,!=
# logical_and、logical_or、logical_xor--执行元素级的真值逻辑运算。相当于中辍运算符 &、|、^
# 示例:
# 一元ufunc函数示例:
# 1)np.sqrt(arr) 计算每个元素的平方根
arr=np.arange(10)
np.sqrt(arr)
array([0. , 1. , 1.41421356, 1.73205081, 2. ,
2.23606798, 2.44948974, 2.64575131, 2.82842712, 3. ])
# 2)np.exp(arr) 计算各元素的以e为底的指数
np.exp(arr)
array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
2.98095799e+03, 8.10308393e+03])
# 3) np.modf(arr) 将数组的小数和整数部分以两个独立数组的形式返回
# 会返回两个数组(返回两个数组的ufunc比较少),它是python内置函数divmod的矢量化版本。
arrfloat=np.random.randn(7)*5
np.modf(arrfloat)
(array([ 0.06999584, 0.51758053, -0.46226613, -0.26251269, 0.36295513,
0.84655061, -0.43529079]),
array([ 4., 1., -6., -3., 5., 1., -2.]))
# 二元ufunc函数示例:
arr1=np.random.randn(8)
arr2=np.random.randn(8)
# 1)np.add(arr1,arr2) 对应位置元素求和
arr1
array([-0.11423455, 0.34311356, 0.97609564, 0.43885802, 1.61820549,
-1.21456404, -0.62405483, -1.37193806])
arr2
array([-0.01736506, 1.5373613 , 1.3406096 , -0.20445385, 0.22836248,
-1.95019508, 1.39529547, 0.39184623])
np.add(arr1,arr2)
array([-0.13159961, 1.88047485, 2.31670524, 0.23440417, 1.84656797,
-3.16475912, 0.77124064, -0.98009183])
# 2)np.maximum(arr1,arr2) 对应位置元素取较大值
np.maximum(arr1,arr2)
array([-0.01736506, 1.5373613 , 1.3406096 , 0.43885802, 1.61820549,
-1.21456404, 1.39529547, 0.39184623])
# 九,使用数组进行面向数组编程
# 9.1--假设我们想得到一组值(网格型)上计算sqrt(x^2+y^2)。np.meshingrid(arr1,arr2)函数接受两个一维数组,并产生两个二维矩阵
# 假设一维数组的长度为n,那么二维数组的shape为(n,n)
#(对应于两个数组中所有的(x,y)对):
points=np.arange(-5,5,0.01) # 一维数组
xs,ys=np.meshgrid(points,points) # xs,ys均为二维数组,
xs
array([[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
...,
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99]])
ys
array([[-5. , -5. , -5. , ..., -5. , -5. , -5. ],
[-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
[-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
...,
[ 4.97, 4.97, 4.97, ..., 4.97, 4.97, 4.97],
[ 4.98, 4.98, 4.98, ..., 4.98, 4.98, 4.98],
[ 4.99, 4.99, 4.99, ..., 4.99, 4.99, 4.99]])
# 现在对函数的求值运算就好办了,把这两个数组当作两个浮点数那样编写表达式即可:
z=np.sqrt(xs**2+ys**2) # xs**2+ys**2是数组间的运算得到一个新数组 然后再sqrt
z
array([[7.07106781, 7.06400028, 7.05693985, ..., 7.04988652, 7.05693985,
7.06400028],
[7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
7.05692568],
[7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
7.04985815],
...,
[7.04988652, 7.04279774, 7.03571603, ..., 7.0286414 , 7.03571603,
7.04279774],
[7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
7.04985815],
[7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
7.05692568]])
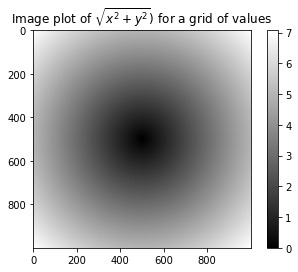
# 作图
import matplotlib.pyplot as plt
plt.imshow(z,cmap=plt.cm.gray);plt.colorbar()
plt.title("Image plot of $\sqrt{x^2+y^2})$ for a grid of values")
Text(0.5, 1.0, 'Image plot of $\\sqrt{x^2+y^2})$ for a grid of values')
# 9.2-- numpy.where() 将条件逻辑表述为数组运算
# 9-2-1)numpy.where(conditionarr,xarr,yarr)函数
# 三个参数都为数组,即python中三元表达式: x if condition else y 的矢量化版本。不改变 conditionarr, xarr,yarr,返回一个新的数组。
# 示例:假设我们有一个布尔数组cond和两个值数组xarr,yarr:
xarr=np.array([1.1,1.2,1.3,1.4,1.5])
yarr=np.array([2.1,2.2,2.3,2.4,2.5])
condarr=np.array([True,False,True,True,False])
np.where(condarr,xarr,yarr)
# np.where(cond,xarr,yarr).tolist() #转化为列表
array([1.1, 2.2, 1.3, 1.4, 2.5])
# 如果使用python的列表推导式,应该是这样做:
results=[(x if cond else y) for x,y,cond in zip(xarr,yarr,cond)] # 得到一个列表
results
# 使用纯python,对于大数组效率特别慢,当xarr和yarr是多维数组时,无能为力。
[1.1, 2.2, 1.3, 1.4, 2.5]
# 9-2-2)当第一参数为数组判断表达式,其余参数不为数组时
# numpy.where(condition,标量1或数组1,标量2或数组2)函数 np.where()函数的第二个和第三个参数可以不必是数组,也可以是标量或标量与数组的组合
# 在数据分析工作中,where通常用于根据一个数组而生成另一个新数组。
# 示例2:假设有一个随机数据组成的矩阵,你希望将所有的正值替换为2,将所有的负值替换为-2,使用where会很简单
arrrandn=np.random.randn(4,4)
np.where(arrrandn>0,2,-2) # 根据一个数组而生成另一个新数组。
array([[-2, 2, 2, 2],
[-2, 2, 2, 2],
[-2, -2, 2, -2],
[-2, 2, 2, -2]])
np.where(arrrandn>0,2,arrrandn) # 只将正数用2替换,其余不变。 # 根据一个数组而生成另一个新数组。
array([[-2.86684263, 2. , 2. , 2. ],
[-0.1251956 , 2. , 2. , 2. ],
[-0.34407839, -0.07410133, 2. , -0.41481679],
[-0.73640143, 2. , 2. , -0.82490141]])
# 9-2-3)np.where(condition)
#只有条件 (condition),没有x和y,则输出满足条件 (即非0) 元素的坐标。
#这里的坐标以数组为元素的tuple的形式给出,通常原数组有多少维,输出的tuple中就包含几个数组,分别对应符合条件元素的各维坐标。
a = np.array([1,3,5,7,9])
print(np.where(a>5)) # (array([3, 4], dtype=int64),) 这是个元组
print(a[np.where(a>5)]) # [7 9] 得到的是列表
# 9-2-4)numpy.where的嵌套使用:
# 两个布尔类型的数组cond1和cond2,如果对应元素都是True,就是11,如果只有第一个数组的元素是True,就是10,
# 如果只有第二个数组的元素是True,就是01,如果两个数组的对应元素都是False元,就是00,用列表接收他们。
results=[]
arr1=np.array([True,False,False,False,True])
arr2=np.array([False,False,True,False,True])
n=arr1.size
for i in range(n):
if arr1[i] and arr2[i]:
results.append('11')
elif arr1[i]:
results.append('10')
elif arr2[i]:
results.append('01')
else:
results.append('00')
results
['10', '00', '01', '00', '11']
# 使用np.where进行嵌套就可以写得更简单:
np.where((arr1 & arr2),'11',np.where(arr1,'10',np.where(arr2,'01','00'))).tolist()
['10', '00', '01', '00', '11']
# 9.3,数学和统计方法 聚合函数和其他函数
# 聚合函数:
# sum 沿着轴向计算所有的累计和,0长度的数组,累计和就是0
# mean 数学平均,0长度的数组平均值是 NAN
# std 标准差,可以选择自由度调整(默认分母是 n)
# var 方差,可以选择自由度调整(默认分母是 n)
# min,max 最小值和最大值
# argmin,argmax 最小值和最大值的位置
# 其他统计方法:
# cumsum 所有元素的累积和,第一个加数为0
# cumprod 所有元素的累积,第一个乘数是1
# 9.3.1 一些聚合函数(也叫缩减函数),比如sum,mean,std(标准差),可以作为数组的实例方法被调用,也可以作为顶级numpy函数使用,
# 对整个数组或某个轴向的数据进行统计计算。
# 比如: arr.mean() 和 np.mean(arr) 效果相同。
# 1)示例 1 对整个数组使用聚合函数:
# 准备一个正态分布的随机数组:
arr=np.random.randn(5,4)
# sum,mean,std的使用:
print(arr.mean(),"--",np.mean(arr))
print(arr.sum(),"--",np.sum(arr))
print(arr.std(),"--",np.std(arr))
0.16849962731538337 -- 0.16849962731538337
3.3699925463076674 -- 3.3699925463076674
0.9828447058023279 -- 0.9828447058023279
# 1)示例 2 对数组的某个轴数据使用聚合函数:
# sum,mean,std的使用: axis=1 可以简写为 1 1表示列轴向(列号递增的方向,其实就是行)
print(arr.mean(axis=1),"--",np.mean(arr,axis=1)) # 计算每一列的平均值
print(arr.sum(axis=1),"--",np.sum(arr,axis=1)) # 计算每一列的和
print(arr.std(axis=1),"--",np.std(arr,axis=1)) # 计算每一列的标准差
[ 0.39721479 -0.53907257 0.80701694 0.02321185 0.15412712] -- [ 0.39721479 -0.53907257 0.80701694 0.02321185 0.15412712]
[ 1.58885916 -2.15629028 3.22806777 0.09284742 0.61650847] -- [ 1.58885916 -2.15629028 3.22806777 0.09284742 0.61650847]
[0.64008158 0.66171982 0.67832542 0.677676 1.44256105] -- [0.64008158 0.66171982 0.67832542 0.677676 1.44256105]
# sum,mean,std的使用:
print(arr.mean(1),"--",np.mean(arr,1)) # 计算每一列的平均值
print(arr.sum(1),"--",np.sum(arr,1)) # 计算每一列的和
print(arr.std(1),"--",np.std(arr,1)) # 计算每一列的标准差
[ 0.39721479 -0.53907257 0.80701694 0.02321185 0.15412712] -- [ 0.39721479 -0.53907257 0.80701694 0.02321185 0.15412712]
[ 1.58885916 -2.15629028 3.22806777 0.09284742 0.61650847] -- [ 1.58885916 -2.15629028 3.22806777 0.09284742 0.61650847]
[0.64008158 0.66171982 0.67832542 0.677676 1.44256105] -- [0.64008158 0.66171982 0.67832542 0.677676 1.44256105]
# sum,mean,std的使用:
print(arr.mean(0),"--",np.mean(arr,0)) # 计算每一行的平均值
print(arr.sum(0),"--",np.sum(arr,0)) # 计算每一行的和
print(arr.std(0),"--",np.std(arr,0)) # 计算每一行的标准差
[ 0.43711985 0.66037716 -0.3156837 -0.1078148 ] -- [ 0.43711985 0.66037716 -0.3156837 -0.1078148 ]
[ 2.18559927 3.30188578 -1.57841849 -0.53907401] -- [ 2.18559927 3.30188578 -1.57841849 -0.53907401]
[0.83383241 0.87271032 1.22192838 0.53762685] -- [0.83383241 0.87271032 1.22192838 0.53762685]
# 9.3.2 其他统计函数(非聚合函数)
# cumsum 所有元素的累计和 第一个加数是0
# umprod 所有元素的累积 第一个乘数是1
# 这两个函数不会使数组聚合,而是会产生一个中间结果的数组,这个数组的长度与原数组的长度一致。
# 示例1--对整个数组使用cumsum,umprod:
arr1=np.array([0,1,2,3,4,5,6,7])
arr1.cumsum()
array([ 0, 1, 3, 6, 10, 15, 21, 28], dtype=int32)
arr1.cumprod()
array([0, 0, 0, 0, 0, 0, 0, 0], dtype=int32)
arr2=np.array([1,2,3,4,5,6,7])
arr2.cumprod()
array([ 1, 2, 6, 24, 120, 720, 5040], dtype=int32)
# 示例2--对数组的某个轴数据使用cumsum,umprod:
arr3=np.arange(9).reshape((3,3))
arr3
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
arr3.cumsum(1) # 1表示列轴向(列号递增的方向,其实就是行)
array([[ 0, 1, 3],
[ 3, 7, 12],
[ 6, 13, 21]], dtype=int32)
arr3.cumprod(1)
array([[ 0, 0, 0],
[ 3, 12, 60],
[ 6, 42, 336]], dtype=int32)
# 9.4,布尔值数组的方法
# 同样,下面的函数既可以作为数组实例的方法被调用,也可以作为顶级numpy函数使用。
# sum(),any(),all()
# 这些函数也可以用于非布尔类型数组,所有非0元素,都会被认为是True.
# 9.4.1 sum()函数
arr=np.random.randn(100)
print((arr>0).sum()) # 49 统计数组中元素大于0的个数 布尔类型数组的True相当于1,False相当于0
print(np.sum(arr>0)) # 49
# 9.4.2 any()和all(), any检查数组中是否至少有一个True,all检查数组中是否全是True
bools=np.array([False,True,False,False])
print(bools.any()) # True
print(np.any(bools)) # True
print(bools.all()) # False
print(np.all(bools)) # False
# 9.5,数组排序
# 和python的内建列表类型相似,Numpy数组可以使用sort方法按位置排序:
# arr.sort() in place sort, 会改变原数组。
# np.sort(arr),np.sort(arr,1) 顶层的np.sort()方法返回的是数组的copy,不会改变原数组。
# 其他排序方法:间接排序(参照高级numpy),与排序相关的其他种类的数据操作,比如根据一个表的某一列排序,(pandas会讲)
# 9.5.1 arr.sort()对整个一维数组排序:
arr=np.random.randn(6)
arr
array([ 0.28791664, -0.33857089, -0.25479571, 0.8856711 , -2.80537025,
3.58768604])
arr.sort()
arr
array([-2.80537025, -0.33857089, -0.25479571, 0.28791664, 0.8856711 ,
3.58768604])
# 9.5.2 arr.sort()对于二维数组排序:
arr2=np.random.randn(5,3)
arr2
array([[ 1.18081678, 0.17371794, 2.37109646],
[ 0.25508294, -1.28392 , -0.29739046],
[ 0.65719139, -1.42167423, 0.06661373],
[ 0.5586866 , -0.64003369, 2.32344008],
[-0.47146893, -0.14909249, -0.42267235]])
arr2.sort() # 当没有参数时,实际默认参数为 1
# arr2.sort(1)
arr2
array([[ 0.17371794, 1.18081678, 2.37109646],
[-1.28392 , -0.29739046, 0.25508294],
[-1.42167423, 0.06661373, 0.65719139],
[-0.64003369, 0.5586866 , 2.32344008],
[-0.47146893, -0.42267235, -0.14909249]])
arr2=np.random.randn(5,3)
arr2
array([[-0.79484895, 0.46884083, 1.53851912],
[ 0.62346424, 0.51440027, 0.22166369],
[ 0.03477362, -1.9244294 , 0.03262501],
[-1.25440832, -0.09754629, -0.81348808],
[-1.11063465, 0.04493534, -1.2358787 ]])
arr2.sort(0)
arr2
array([[-1.25440832, -1.9244294 , -1.2358787 ],
[-1.11063465, -0.09754629, -0.81348808],
[-0.79484895, 0.04493534, 0.03262501],
[ 0.03477362, 0.46884083, 0.22166369],
[ 0.62346424, 0.51440027, 1.53851912]])
# 9.5.3 np.sort(arr),np.sort(arr,axis=1) ,np.sort(arr,axis=0)
# 只拿一维数组来举例:
arr=np.random.randn(6)
arr
array([-0.00642429, -0.17085358, -0.09756021, -0.26958744, -0.29145018,
-0.8358323 ])
np.sort(arr) # 返回新的数组,不改变原数组
array([-0.8358323 , -0.29145018, -0.26958744, -0.17085358, -0.09756021,-0.00642429])
arr
array([-0.00642429, -0.17085358, -0.09756021, -0.26958744, -0.29145018,-0.8358323 ])
# 9.6,唯一值与其他集合逻辑
# Numpy 包含一些针对一维 ndarray 的基础集合操作。
# 注,都是numpy的顶层方法,ndarray对象不存在这些方法。
# np.unique(arr) 计算arr的唯一值,并排序
# np.intersect1d(arr1,arr2) 计算两个数组的交集,并排序
# np.union1d(arr1,arr2) 计算两个数组的并集,并排序
# np.ind1d(arr1,arr2) 计算arr1的元素,是否存在于arr2中
# np.setdifferent(arr1,arr2) 差集,在arr1中,但不在arr2中的元素
# np.setxor1d(arr1,arr2) 异或集,在arr1中或在arr2中,但不在二者的交集中
# 以下只针对 np.unique(arr) np.in1d(arr1,arr2) 进行讲解:
# 9.6.1 np.unique(arr) 返回的是数组中唯一值排序(去重后排序)后形成的数组。
names=np.array(['Bob','Joe','Will','Bob','Will','Joe','Joe'])
np.unique(names)
# names.unique() 这种用法不存在
array(['Bob', 'Joe', 'Will'], dtype='<U4')
ints=np.array([3,3,3,2,2,1,1,4,4])
np.unique(ints)
array([1, 2, 3, 4])
# 用纯python 来实现上面的例子:
# 使用set()函数,将数组转化为set集合,自动去重,然后用sorted()函数对set集合排序,得到列表:
# 知识点:set(ndarray对象)得到去重后的set集合, sorted(set)得到排序后的列表。
names=np.array(['Bob','Joe','Will','Bob','Will','Joe','Joe'])
names_set=set(names)
sorted(names_set)
['Bob', 'Joe', 'Will']
ints=np.array([3,3,3,2,2,1,1,4,4])
ints_set=set(ints)
sorted(ints_set)
[1, 2, 3, 4]
# 9.6.2 np.in1d(arr1,arr2)
# 用来检查一个数组中的值是否在另外一个数组中也出现,并返回一个和第一个数组长度一致的布尔类型数组。
values01=np.array([5,6,7,9,0,0,3])
values02=np.array([5,8,7,5])
np.in1d(values01,values02)
array([ True, False, True, False, False, False, False])
Numpy_01的更多相关文章
- 【341】Numpy 相关应用
Numpy_01 >>> from numpy import pi >>> np.linspace(0, 2, 9) array([0. , 0.25, 0.5 , ...
随机推荐
- shell-的变量-局部变量
1. 定义本地变量 本地变量在用户当前的shell生产期的脚本中使用.例如,本地变量OLDBOY取值为ett098,这个值只在用户当前shell生存期中有意义.如果在shell中启动另一个进程或退出, ...
- navicat 生成注册码( 仅供学习使用 )
前言,由于navicat使用比较顺手,刚好前段时间试用期到,又看看了怎么生成注册码,特地记录下使用 . 1.运行 找到 navicat 文件(exe) 2.生成注册文件(报错好,后续会用到) 3.断网 ...
- 【找规律】ARC 066D Xor Sum AtCoder - 2272
题目大意 给出一个整数\(n\),已知\(0\le u,v\le n\),求满足\(a\ xor\ b=u\)且\(a+b=v\)的\(a.b\)对数 样例1输入 3 样例1输出 5 /* u=0,v ...
- linux(centos8):安装kubernetes worker节点并加入到kubernetes集群(kubernetes 1.18.3)
一,安装kubernetes前的准备工作 安装前的准备工作(master\worker都要进行) 参见: https://www.cnblogs.com/architectfore ...
- LUMEN框架多数据库连接配置方法
LUMEN作为一款API导向很浓的框架,配置极简化,默认只支持一路DB配置 然而随着业务复杂度的提高,引入多个数据库连接似乎无法避免,下面介绍一下LUMEN连接多个数据库的配置方法: 修改.env文件 ...
- django—Form组件校验方法(is_valid)执行流程
1.从is_valid方法入手 def is_valid(self): """Return True if the form has no errors, or Fals ...
- Sentinel流控规则
流控规则 注:Sentinel的监控页面一开始是没有东西,需要对监控的服务发起请求后才会出现 资源名:唯一名称,默认请求路径 针对来源:Sentinel可以针对调用者进行限流,填写微服务名,指定对哪个 ...
- Bitmap缩放(三)
质量压缩 public class MainActivity extends AppCompatActivity { @Override protected void onCreate(Bundle ...
- ERP应收应付的操作与设计--开源软件诞生21
赤龙ERP应收应付讲解--第21篇 用日志记录"开源软件"的诞生 [点亮星标]----祈盼着一个鼓励 博主开源地址: 码云:https://gitee.com/redragon/r ...
- D. Alyona and Strings 解析(思維、DP)
Codeforce 682 D. Alyona and Strings 解析(思維.DP) 今天我們來看看CF682D 題目連結 題目 略,請直接看原題. 前言 a @copyright petjel ...
