CMU数据库(15-445)-实验2-B+树索引实现(中）删除

3. Delete 实现

附上实验2的第一部分 https://www.cnblogs.com/JayL-zxl/p/14324297.html

3. 1 删除算法原理

如果叶子结点中没有相应的key，则删除失败。否则执行下面的步骤

图片来自于这篇博文https://www.programiz.com/dsa/deletion-from-a-b-plus-tree

情况1 要删除的要素就只在叶子结点
1. 删除叶子结点中对应的key。删除后若结点的key的个数大于等于\(\frac{m-1}{2}\)，删除操作结束。
  
  删除40的例子如下
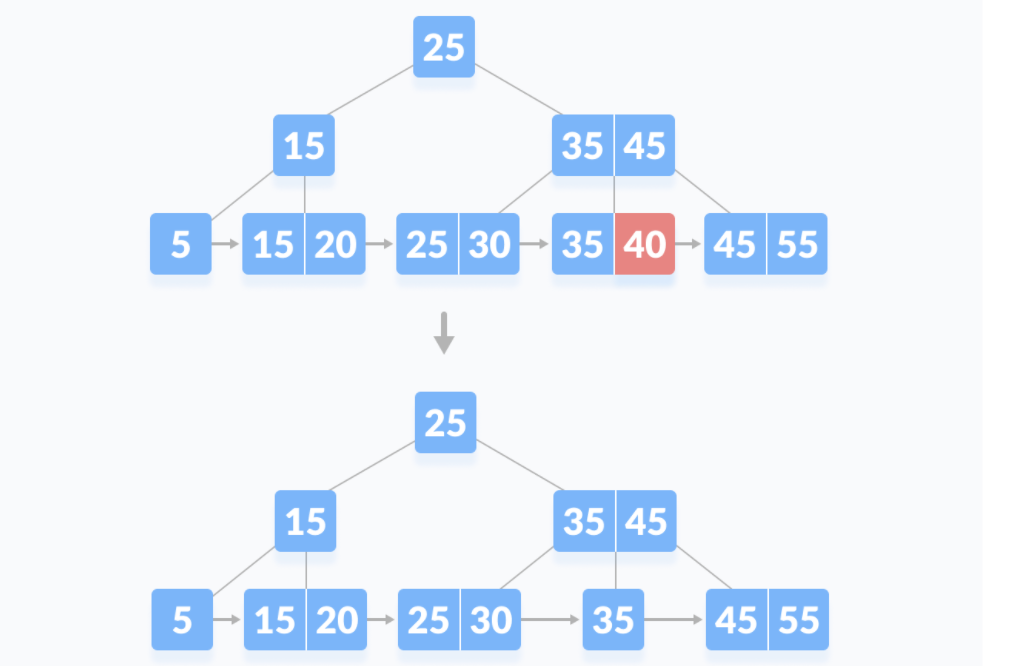
2. 若兄弟结点key有多余（\(>\frac{m-1}{2}\)），向兄弟结点借一个关键字，然后用兄弟结点的median key替代父结点。
  
  删除5的例子如下
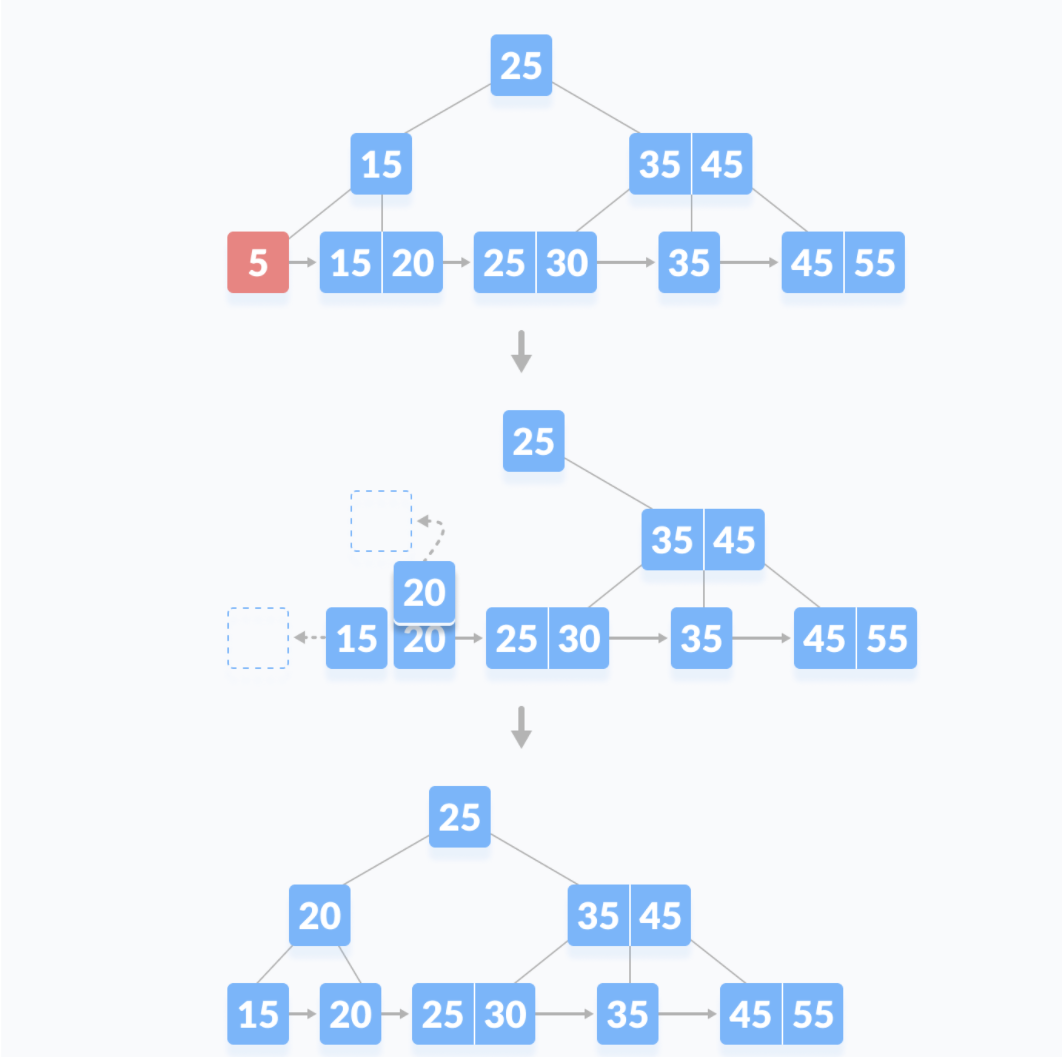
情况2 要删除的元素不仅在叶子结点而且在内部结点出现
1. 如果结点中的元素个数\(> \frac{m-1}{2}\)，只需从叶结点删除key值，同时从内部节点删除键。用key元素的后继元素补充内部节点的空余空间。
  
  删除45
2. 如果节点中元素个数等于\(\frac{m-1}{2}\)，则删除该键并从其直接兄弟借一个键。用借来的键填充内部结点中所形成的空空间。
  
  删除35
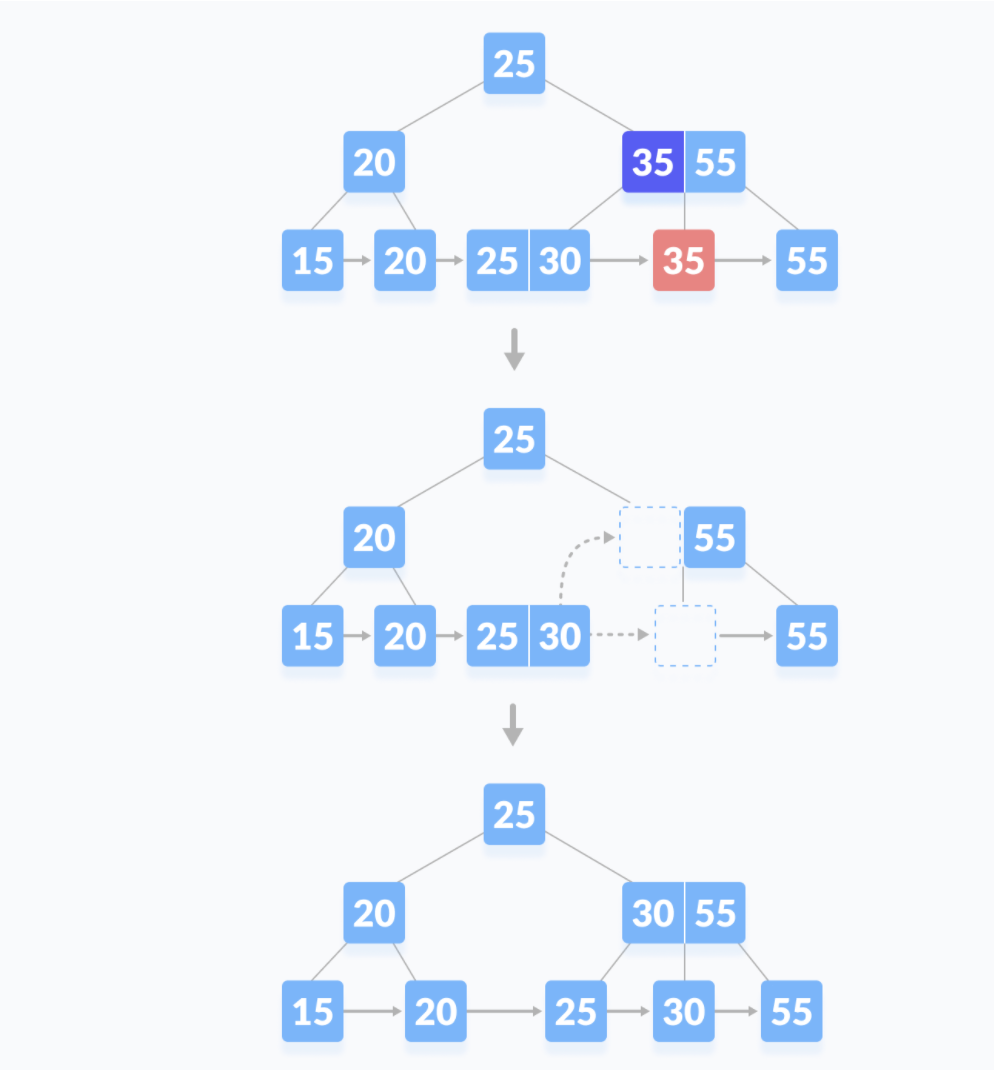
3. 和情况2的第一种情况类似。只不过空洞结点是当前结点的祖父结点。
  
  删除25
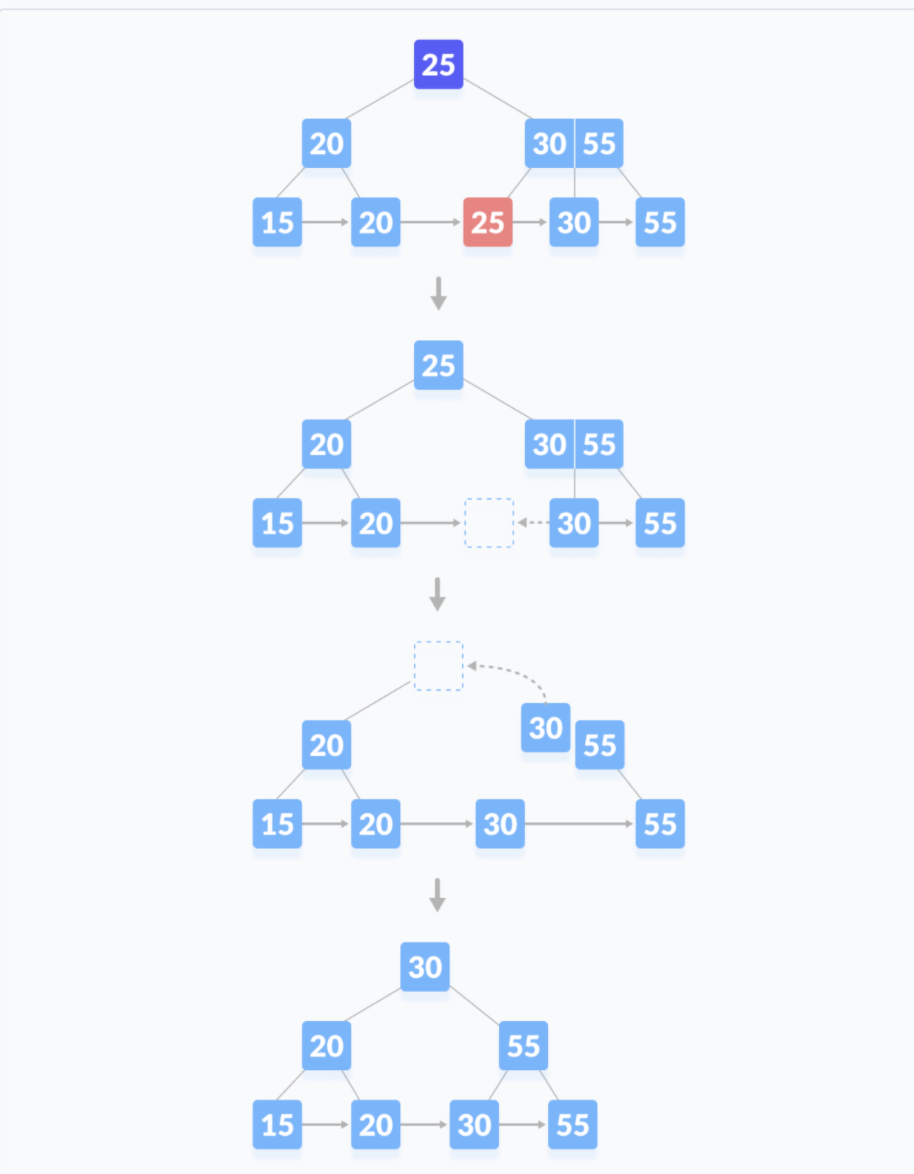
情况3 这种情况是树的高度会缩小的情况。

这种情况有点复杂。请看删除55的例子

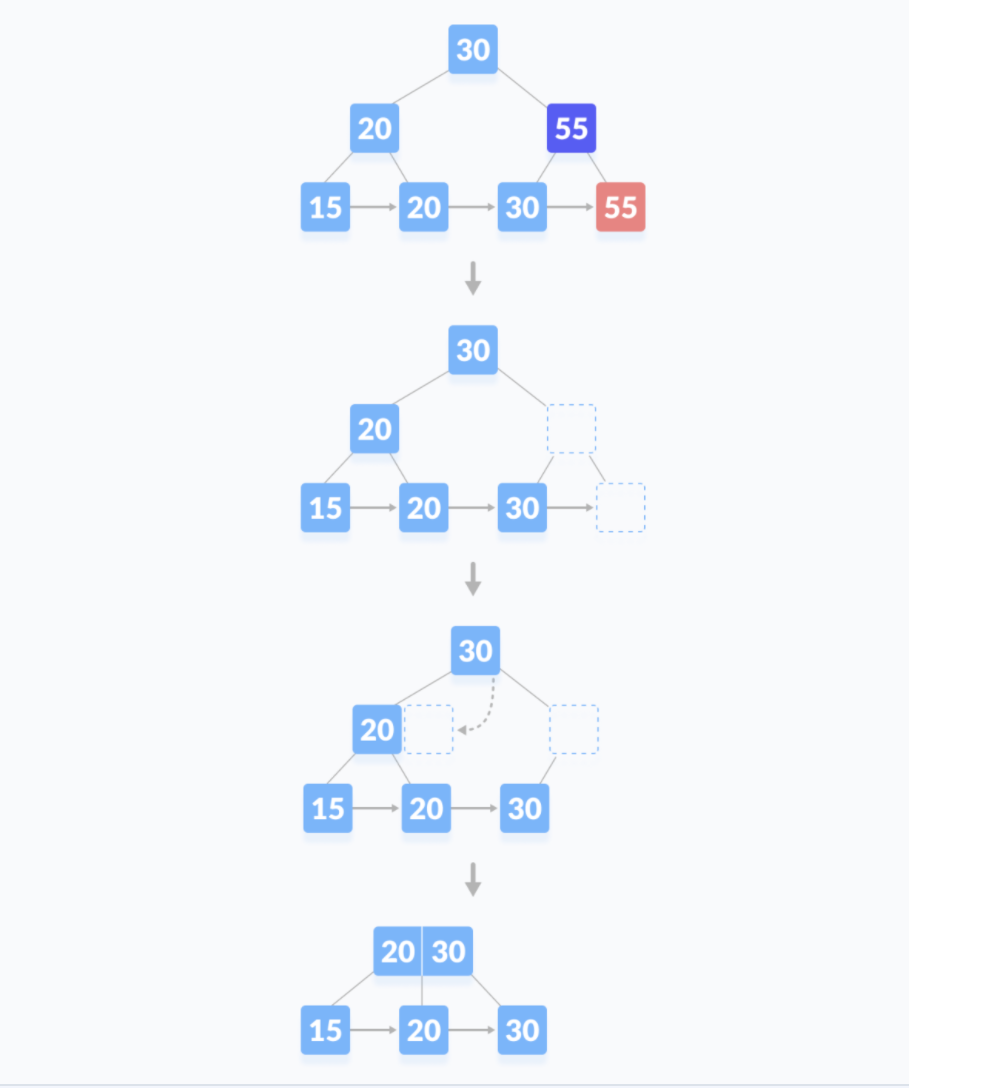
cmu这里给了演示网站 https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

算法描述见下表

3.2 删除算法实现

如果当前是空树则立即返回
否则先找到要删除的key所在的page

随后调用RemoveAndDeleteRecord在叶page上直接删除key值

同样还是经典的二分查找

INDEX_TEMPLATE_ARGUMENTS

int B_PLUS_TREE_LEAF_PAGE_TYPE::RemoveAndDeleteRecord(const KeyType &key, const KeyComparator &comparator) {

  int l=0,r=GetSize()-1;

  if(l>r||comparator(key,array[l].first)<0||comparator(key,array[r].first)>0)return GetSize();

  while(l<=r){

    int mid=(l+r)>>1;

    if(comparator(key, KeyAt(mid)) < 0){

      r=mid;

    }

    else if (comparator(key, KeyAt(mid)) > 0) l=mid+1;

    else{

      memmove(array + mid, array + mid + 1,static_cast<size_t>((GetSize() - mid - 1)*sizeof(MappingType)));

      IncreaseSize(-1);

      break;

    }

  }

  return GetSize();

}

删除之后的叶子结点有两种情况

叶子结点内关键字个数小于最小值向下执行。否则结束

-- 调用CoalesceOrRedistribute

1.如果当前结点是根节点则调用AdjustRoot(node)

INDEX_TEMPLATE_ARGUMENTS

bool BPLUSTREE_TYPE::AdjustRoot(BPlusTreePage *old_root_node) {

  //case 2

  if (old_root_node->IsLeafPage()) {

    if (old_root_node->GetSize() == 0) {

      root_page_id_ = INVALID_PAGE_ID;

      UpdateRootPageId(false);

      return true;

    }

    return false;

  }

  //  case 1

  if (old_root_node->GetSize() == 2) {

    auto root =reinterpret_cast<BPlusTreeInternalPage<KeyType, page_id_t,KeyComparator> *>(old_root_node);

    root_page_id_ = root->ValueAt(1);

    UpdateRootPageId(false);

    auto page = buffer_pool_manager_->FetchPage(root_page_id_);

    if (page == nullptr) {

      throw "no page can used while AdjustRoot";

    }

    auto new_root =reinterpret_cast<BPlusTreeInternalPage<KeyType, page_id_t,KeyComparator> *>(page);

    new_root->SetParentPageId(INVALID_PAGE_ID);

    buffer_pool_manager_->UnpinPage(root_page_id_, true);

    return true;

  }

  return false;

}

2.否则应该找它的兄弟节点

默认都是找它左边的结点。如果当前已经在最左边即第一个我们找右边的结点

调用CoalesceOrRedistribute

a. 如果兄弟结点的size+当前结点的size大于最大值则需要重新分配

-- 调用Redistribute函数

INDEX_TEMPLATE_ARGUMENTS

template <typename N>

bool BPLUSTREE_TYPE::CoalesceOrRedistribute(N *node, Transaction *transaction) {

  if (node->IsRootPage()) {

    return AdjustRoot(node);

  }

  if (node->IsLeafPage()) {

    if (node->GetSize() >= node->GetMinSize()) {

      return false;

    }

  } else {

    if (node->GetSize() > node->GetMinSize()) {

      return false;

    }

  }

  auto page = buffer_pool_manager_->FetchPage(node->GetParentPageId());

  if (page == nullptr) {

    throw "no page can used while CoalesceOrRedistribute";

  }

  auto parent =reinterpret_cast<BPlusTreeInternalPage<KeyType, page_id_t,KeyComparator> *>(page);

  int value_index = parent->ValueIndex(node->GetPageId());

  //sibling page  always find left page

  int sibling_page_id;

  if (value_index == 0) {

    sibling_page_id = parent->ValueAt(value_index + 1);

  } else {

    sibling_page_id = parent->ValueAt(value_index - 1);

  }

  // fetch sibling node

  auto sibling_page = buffer_pool_manager_->FetchPage(sibling_page_id);

  if (sibling_page == nullptr) {

    throw Exception("all page are pinned while CoalesceOrRedistribute");

  }

  // put sibling node to PageSet

  sibling_page->WLatch();

  transaction->AddIntoPageSet(sibling_page);

  auto sibling = reinterpret_cast<N *>(sibling_page);

  bool is_redistribute = false;

  // If sibling's size + input

  //  page's size > page's max size, then redistribute.

  if (sibling->GetSize() + node->GetSize() > node->GetMaxSize()) {

    is_redistribute = true;

    //TODO need to modify parent

    buffer_pool_manager_->UnpinPage(parent->GetPageId(), true);

  }

  // exec  redistribute

  if (is_redistribute) {

    Redistribute<N>(sibling, node, value_index);

    return false;

  }

 //Otherwise, merge.

  bool ret;

  if (value_index == 0) {

    Coalesce<N>(node, sibling, parent, 1, transaction);

    transaction->AddIntoDeletedPageSet(sibling_page_id);

    // node should not be deleted

    ret = false;

  } else {

    Coalesce<N>(sibling, node, parent, value_index, transaction);

    // node should be deleted

    ret = true;

  }

  //TODO unpin parent

  buffer_pool_manager_->UnpinPage(parent->GetPageId(), true);

  return ret;

}

重新分配的时候有两种情况

(1) 移动它左边结点最大的的元素到当前结点的第一个元素---对应MoveLastToFrontOf函数

这里20年版本的实验把之前版本的传递index改成了传递key值的引用。并且没有等号可以用，emm为了偷懒我把它改成了和17年实验一样的设置，这里注意对于实验给你的头文件好多需要修改。不然模版类就会报错

注意这里对于internalPage和LeafPage并不一样

首先看对于LeafPage的实现

整体逻辑非常简单

就是把元素append到末尾
然后就是修改父亲结点的元素。

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_LEAF_PAGE_TYPE::MoveLastToFrontOf(BPlusTreeLeafPage *recipient,int parentIndex,

                                                   BufferPoolManager *buffer_pool_manager) {

  MappingType pair = GetItem(GetSize() - 1);

  IncreaseSize(-1);

  recipient->CopyFirstFrom(pair, parentIndex, buffer_pool_manager);

}

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_LEAF_PAGE_TYPE::CopyFirstFrom(const MappingType &item, int parentIndex,

                                               BufferPoolManager *buffer_pool_manager) {

  assert(GetSize() + 1 < GetMaxSize());

  memmove(array + 1, array, GetSize()*sizeof(MappingType));

  IncreaseSize(1);

  array[0] = item;

  auto page = buffer_pool_manager->FetchPage(GetParentPageId());

  if (page == nullptr) {

    throw "no page can used while CopyFirstFrom";

  }

  // get parent

  auto parent =reinterpret_cast<BPlusTreeInternalPage<KeyType, decltype(GetPageId()),KeyComparator> *>(page->GetData());

  parent->SetKeyAt(parentIndex, item.first);

  buffer_pool_manager->UnpinPage(GetParentPageId(), true);

}

然后看对于InternalPage的实现

这里和leafpage不一样的就是最后一个元素在GetSize()处
这里要修改移动元素value值（所指向的结点）的parent结点

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_INTERNAL_PAGE_TYPE::MoveLastToFrontOf(BPlusTreeInternalPage *recipient,  int parent_index,

                                                       BufferPoolManager *buffer_pool_manager) {

  assert(GetSize() > 1);

  IncreaseSize(-1);

  MappingType pair = array[GetSize()];

  page_id_t child_page_id = pair.second;

  recipient->CopyFirstFrom(pair,parent_index, buffer_pool_manager);

  // update parent page id

  auto page = buffer_pool_manager->FetchPage(child_page_id);

  if (page == nullptr) {

    throw "no page can used while MoveLastFrontOf";

  }

  //把要移动元素所指向的结点的parent指针修改。

  auto child = reinterpret_cast<BPlusTreePage *>(page->GetData());

  child->SetParentPageId(recipient->GetPageId());

  assert(child->GetParentPageId() == recipient->GetPageId());

  buffer_pool_manager->UnpinPage(child->GetPageId(), true);

}

/* Append an entry at the beginning.

 * Since it is an internal page, the moved entry(page)'s parent needs to be updated.

 * So I need to 'adopt' it by changing its parent page id, which needs to be persisted with BufferPoolManger

 */

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_INTERNAL_PAGE_TYPE::CopyFirstFrom(const MappingType &pair, int parent_index,BufferPoolManager *buffer_pool_manager) {

  assert(GetSize() + 1 < GetMaxSize());

  auto page = buffer_pool_manager->FetchPage(GetParentPageId());

  if (page == nullptr) {

    throw "no page can used while CopyFirstFrom";

  }

  auto parent = reinterpret_cast<BPlusTreeInternalPage *>(page->GetData());

  auto key = parent->KeyAt(parent_index);

  // set parent key to the last of current page

  parent->SetKeyAt(parent_index, pair.first);

  InsertNodeAfter(array[0].second, key, array[0].second);

  array[0].second = pair.second;

  buffer_pool_manager->UnpinPage(parent->GetPageId(), true);

}

(2) 移动它右边结点最小的元素到当前结点的最后一个元素---对应了MoveFirstToEndOf函数

注意这里对于internalPage和LeafPage并不一样

首先看对于LeafPage的实现

取右边的第一个元素，然后把其他元素都向前移动一个位置(用memmove实现)
然后调用CopyLastFrom函数把元素拷贝过去
随后修改node对应parent的key值

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_LEAF_PAGE_TYPE::MoveFirstToEndOf(BPlusTreeLeafPage *recipient,BufferPoolManager *buffer_pool_manager) {

  MappingType pair = GetItem(0);

  IncreaseSize(-1);

  memmove(array, array + 1, static_cast<size_t>(GetSize()*sizeof(MappingType)));

  recipient->CopyLastFrom(pair);

  auto page = buffer_pool_manager->FetchPage(GetParentPageId());

  if (page == nullptr) {

    throw "no page can used while MoveFirstToEndOf";

  }

  auto parent =reinterpret_cast<BPlusTreeInternalPage<KeyType, decltype(GetPageId()),KeyComparator> *>(page->GetData());

  parent->SetKeyAt(parent->ValueIndex(GetPageId()), pair.first);

  buffer_pool_manager->UnpinPage(GetParentPageId(), true);

}

/*

 * Copy the item into the end of my item list. (Append item to my array)

 */

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_LEAF_PAGE_TYPE::CopyLastFrom(const MappingType &item) {

  assert(GetSize() + 1 <= GetMaxSize());

  array[GetSize()] = item;

  IncreaseSize(1);

}

然后看对于InternalPage的实现

这里需要注意的是internalPage的一个key是在index=1的位置(因为第一个位置就是一个没有key值的指针位置)
因为是内部页，所以要修改它的孩子结点的指向。
还要修改内部结点父结点对应的key

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_INTERNAL_PAGE_TYPE::MoveFirstToEndOf(BPlusTreeInternalPage *recipient,BufferPoolManager *buffer_pool_manager) {

  assert(GetSize() > 1);

  MappingType pair{KeyAt(1), ValueAt(0)};

  page_id_t child_page_id = ValueAt(0);

  SetValueAt(0, ValueAt(1));

  Remove(1);

  recipient->CopyLastFrom(pair, buffer_pool_manager);

  // update child parent page id

  auto page = buffer_pool_manager->FetchPage(child_page_id);

  if (page == nullptr) {

    throw "no page can  used while MoveFirstToEndOf";

  }

  auto child = reinterpret_cast<BPlusTreePage *>(page);

  child->SetParentPageId(recipient->GetPageId());

  assert(child->GetParentPageId() == recipient->GetPageId());

  buffer_pool_manager->UnpinPage(child->GetPageId(), true);

}

/* Append an entry at the end.

 * Since it is an internal page, the moved entry(page)'s parent needs to be updated.

 * So I need to 'adopt' it by changing its parent page id, which needs to be persisted with BufferPoolManger

 */

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_INTERNAL_PAGE_TYPE::CopyLastFrom(const MappingType &pair, BufferPoolManager *buffer_pool_manager) {

  assert(GetSize() + 1 <= GetMaxSize());

  auto page = buffer_pool_manager->FetchPage(GetParentPageId());

  if (page == nullptr) {

    throw Exception("all page are pinned while CopyLastFrom");

  }

  auto parent = reinterpret_cast<BPlusTreeInternalPage *>(page);

  auto index = parent->ValueIndex(GetPageId());

  auto key = parent->KeyAt(index + 1);

  array[GetSize()] = {key, pair.second};

  IncreaseSize(1);

  parent->SetKeyAt(index + 1, pair.first);

  buffer_pool_manager->UnpinPage(parent->GetPageId(), true);

}

b.否则需要进行merge操作

-- 调用Coalesce函数

Coalesce函数比较简单
首先把node结点的所有元素都移动到它的兄弟节点上
调整父结点。也就是把array向前移动
递归调用CoalesceOrRedistribute函数

INDEX_TEMPLATE_ARGUMENTS

template <typename N>

void BPLUSTREE_TYPE::Coalesce(N *neighbor_node, N *node,BPlusTreeInternalPage<KeyType, page_id_t, KeyComparator> *parent,int index, Transaction *transaction) {

  // assumption: neighbor_node is predecessor of node

  //LOG_DEBUG("index %d",index);

  node->MoveAllTo(neighbor_node,index,buffer_pool_manager_);

  LOG_DEBUG("size %d",node->GetSize());

  // adjust parent

  parent->Remove(index);

  //recursive

  if (CoalesceOrRedistribute(parent, transaction)) {

    transaction->AddIntoDeletedPageSet(parent->GetPageId());

  }

}

Internal内的 Remove函数

INDEX_TEMPLATE_ARGUMENTS

void B_PLUS_TREE_INTERNAL_PAGE_TYPE::Remove(int index) {

  assert(0 <= index && index < GetSize());

  memmove(array+index,array+index+1,(GetSize()-index-1)*sizeof(MappingType));

  IncreaseSize(-1);

}

好了删除算法已经实现了。首先我们可以通过test函数

cd build

make b_plus_tree_delete_test

./test/b_plus_tree_delete_test --gtest_also_run_disabled_tests

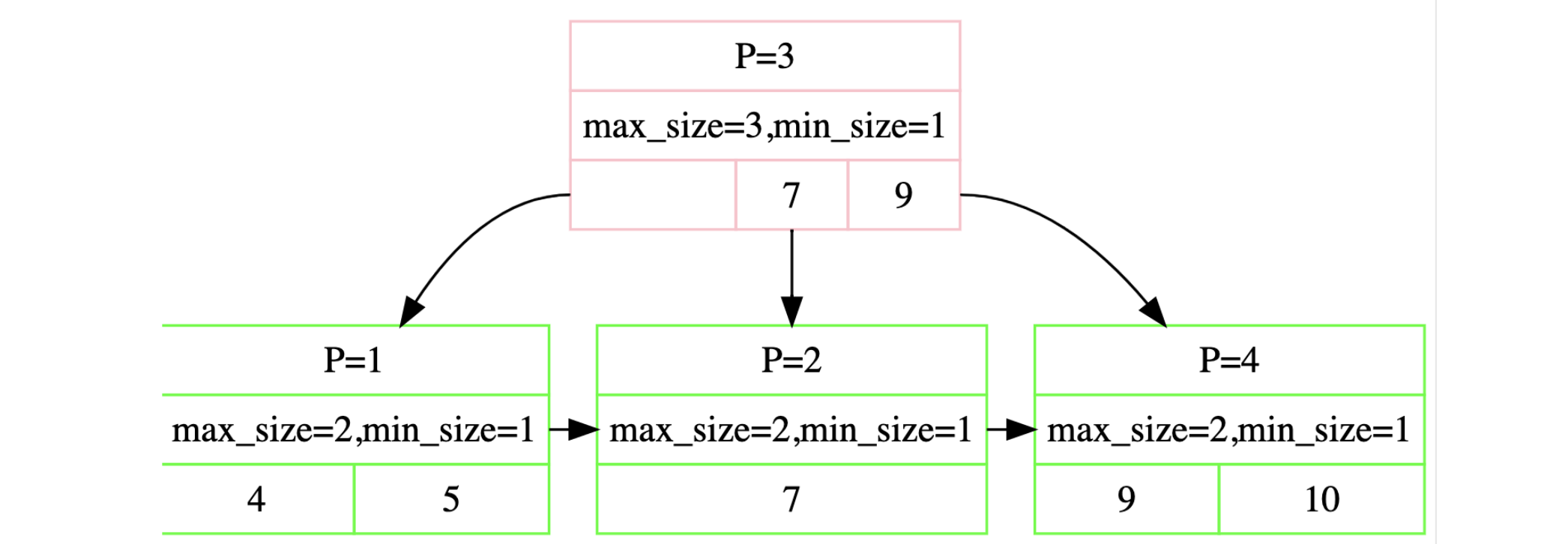
然后我们自己做一些test。这里我就拿一个例子来看

插入10、5、7、4、9得到下图是正确的

然后删除元素7

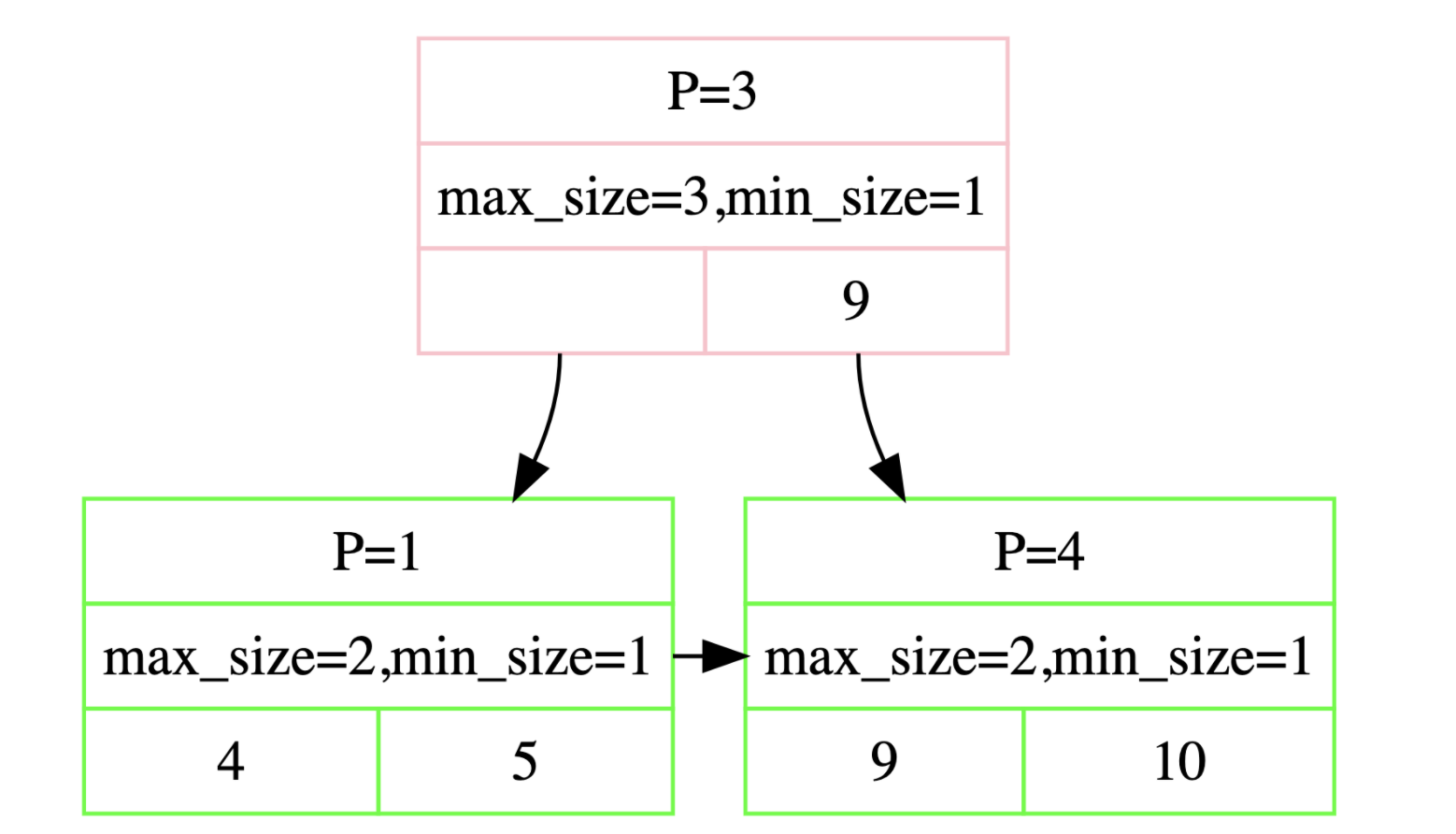
可以发现是完全正确的好了。第二部分就完成了。下面就是最后一部分对于的实现和迭代器的实现