二叉堆python实现

二叉堆是一种完全二叉树，我们可以使用列表来方便存储，也就是说，用列表将树的所有节点存储起来。

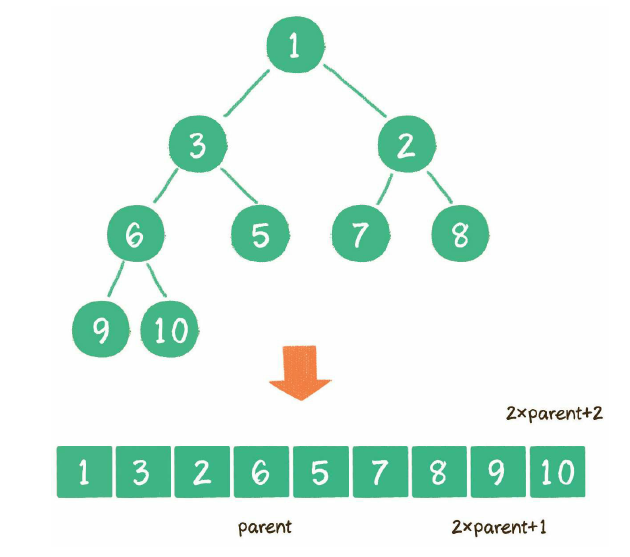
如下图，是小根堆方式的二叉堆，假设父节点的下标为p，则他的左孩子下标为2P+1,右孩子下标为2P+2

class BuildHeap:
    """构建一个小根堆二叉树
    预先定义一个下标为0的元素，实际没有用途，只是为了方便计算乘除
    假设节点下标为i 父节点下标为i//2 左子节点2i 右子节点2i+1
    不加下标为0时，假设父节点下标i，子节点为2i+1，右子节点2i+2
    """

    def __init__(self):
        # 下标0的元素没有用,但为了后面代码可以用到简单的整数
        # 乘除法，仍保留它。
        self.heaplist = [0]
        self.current_size = 0

    def size(self):
        return len(self.heaplist)

    def percUp(self, i):
        """上浮"""
        while i // 2 > 0:
            if self.heaplist[i] < self.heaplist[i // 2]:
                # 与父节点交换。
                self.heaplist[i], self.heaplist[i // 2] = self.heaplist[i // 2], self.heaplist[i]
                i // 2  # 沿路径向上

    def insert(self, key):
        self.heaplist.append(key)  # 添加到末尾
        self.current_size += 1
        self.percUp(self.current_size)  # 新key上浮

    def percDown(self, i):
        """下沉"""
        while (i * 2) <= self.current_size:
            mc = self.minChild(i)
            if self.heaplist[i] > self.heaplist[mc]:
                # 交换，下沉
                self.heaplist[i], self.heaplist[mc] = self.heaplist[mc], self.heaplist[i]
            i = mc  # 沿路径向下

    def minChild(self, i):
        """找最小的子节点"""

        # 判断叶子节点的情况
        if i * 2 + 1 > self.current_size:
            return i * 2
        # 返回较小的子节点
        elif self.heaplist[i * 2] < self.heaplist[i * 2 + 1]:
            return i * 2
        else:
            return i * 2 + 1

    def delMin(self):
        """移走整个堆中最小的key:根节点heapList[1]"""
        retval = self.heaplist[1]  # 移走堆顶
        # 最后的叶子节点移到堆顶，然后size-1，把叶子节点删除
        self.heaplist[1] = self.heaplist[self.current_size]
        self.current_size -= 1
        self.heaplist.pop()
        self.percDown(1)  # 新顶下沉
        return retval

    def buildHeap(self, alist):
        """利用下沉法，构建堆"""
        i = len(alist) // 2  # 从最后节点的父节点开始。
        self.current_size = len(alist)
        self.heaplist = [0] + alist[:]

        while i > 0:
            self.percDown(i)
            i -= 1

import random
l = [i for i in range(1,6)]
random.shuffle(l)
bh = BuildHeap()
bh.buildHeap(l)
l_sort = []
for i in range(1,bh.size()):
    l_sort.append(bh.delMin())

print(l_sort)