从头学起Verilog（一）：组合逻辑基础与回顾

引言

　该部分主要回顾了本科时数字电路中组合逻辑电路部分，内容相对简单和基础。

　内容主要包括：布尔代数相关知识，卡诺图，最大项与最小项，竞争和冒险以及一些常见模块

数字电路中的逻辑

　组合逻辑：输出可以表示为瞬时输入变量的布尔函数。→即输出仅有当前输入决定

　时序逻辑：输出与之前的历史输入（当前状态）有关。→需要相应的存储单元

　正逻辑：高电平为1，低电平为0

　负逻辑：高电平为0，低电平为1

布尔代数

　常用算符（不多赘述）

　代数法则

　　本科时的数电考试，这部分被玩出了花样。但个人感觉除了要考试的学生需要额外练习一下，没有必要去刻意的记，用着用着自然就熟悉了。

　　德摩根定律还是有必要注意一下的，不要把公式作为负担，要当成艺术。

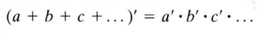
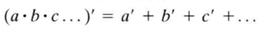
表示法与卡诺图

　表示法

　　这部分展开讲其实没什么意思，但卡诺图，译码器等都要用到。下面以三变量为示例大致说一下。

　　布尔函数可以表示“最小项之和”或“最大项之积”的形式，最大项和最小项个数均为2ⁿ

　　最小项：a’b’c’、a’b’c、a’bc’、ab’c、ab’c’、ab’c、abc’、abc ，分别为m₀ ~ m₇

　　最大项：a’+b’+c’、a’+b’+c、a’+b+c’、a’+b+c、a+b’+c’、a+b’+c、a+b+c’、a+b+c

　　如F=a’b’c’ + a’bc’ + ab’c’ ,可以表示为F=m₀ + m₂ + m₄ = ∑ m（0，2，4）

　　　F=（a’+b’+c）（a’+b+c’）（a+b’+c’）= Π M（1，2，4）

　　关系：1、m_i=M_i'（可以根据德摩根定律得出）

　　　　　2、F=∑ m（0，2，4）也可以写成F=Π M（1，3，5，6，7），两者表达式互补

　　注：若函数表达式F中，仅有非常少的组合能使F值为真，用最小项表示F更高效

　　　　若函数表达式F中，仅有非常少的组合能使F值为假，用最大项表示F'更高效

　　　　这一点在两者关系中可以看出，后面卡诺图中也可能会用到。

　卡诺图

　　卡诺图是一种适用于6或5个变量以下的逻辑化简（相对比较繁琐，大量手工工作）。

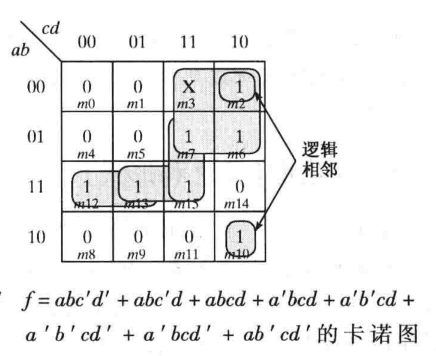
　　如图展示了四变量卡诺图（其中X表示任意项，圈的时候既可作0又可作1）的画法，其中注意顺序是00-01-11-10。

　　化简步骤：1、将布尔表达式F表示为最小项之和的形式，并在最小项处填入1

　　　　　　　2、圈相邻的1（圈尽可能大、每个圈元素个数只能是2的幂、完成后要包含所有1的元素）。注：00和10也是相邻

　　　　　　　3、根据所圈的1，写出对应项并且相或。上图可化简为：F=abc' + abd + a'c + b'cd'

　　上面介绍了将布尔表达式化简成“积之和”形式的方法，当然我们也可以利用卡诺图化成“和之积”的形式

　　

　　化简步骤：1、将布尔表达式F表示为最小项之和的形式，并在最小项处填入1

　　　　　　　2、圈相邻的0，要求同上

　　　　　　　3、根据所圈的0，写出对应项并且相或。下图可写为：F‘=a'c' + b'c' + ab'd + abcd'

　　　　　　　4、F'取反得到F=(a+c)(b+c)(a'+b+c')(a'+b'+c'+d)  　　这里运用了德摩根定律

　任意项与扩展卡诺图

　　任意项x在电路设计中是十分常见的，常用来表示该取值在系统中取不到或者不关心，所以我们可以充分利用这一特点，把任意项x当作0或者1，在卡诺图中圈出更大的圈，从而进一步化简。

　　扩展卡诺图是指通过填入变量的方法将卡诺图扩展（填入一个变量则增加一阶），化简步骤可总结为如下：

　　　　1、表达式化为积之和形式，填入卡诺图，存在的变量保留

　　　　2、令变量均为0，圈1（可利用无关项），得到F₀

　　　　3、将一个变量f₁保留，其余变量为0，所有1变为无关项，利用无关项，圈出包含变量f₁的最大圈，得到F₁

　　　　　  每个变量重复上述步骤，得到一系列F_n

　　　　4、将上述F_n相或，得到结果F=F^₀+F₁+F₂+F₃……

　　

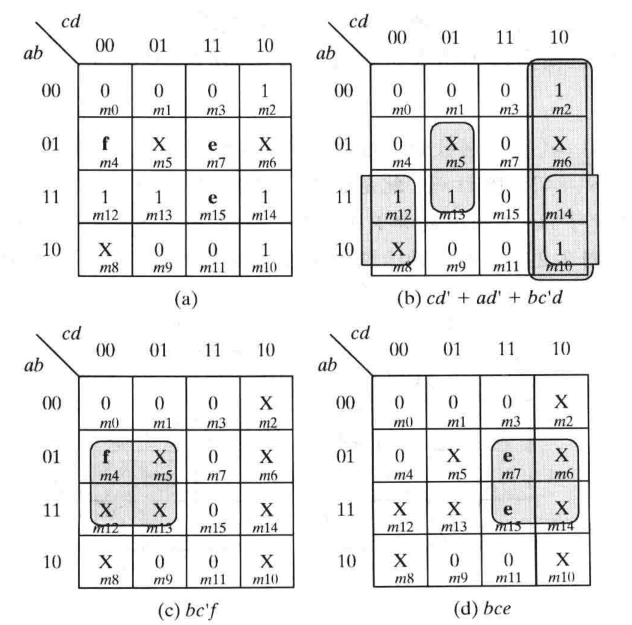
　　如上例：

　　　（a）为将布尔表达式填入后所得卡诺图，f和e为变量

　　　（b）f和e都变为0，圈出1，得到cd'+ad'+bc'd

　　　（c）f保留，e变为0，1变为x，圈出包含f的最大圈，得到bc'f

　　　（d）e保留，f变为0，1变为x，圈出包含e的最大圈，得到bce

　　　（e）得到最终表达式F=cd'+ad'+bc'd+bc'f+bce

竞争和冒险

　　  竞争：不同扇出路径上，到达电路中某一会合点的时间有先有后

　　冒险：施加某些输入信号情况下可能产生毛刺的现象

　　静态冒险：不同扇出路径上的传播时延导致（时钟频率不是很高的情况下，对于时序逻辑几乎不会影响）

　　动态冒险：期望的输入，输出在到达期望值之前发生多次变化（即输入导致了输出稳定前产生了波动）——>静态冒险汇聚的结果——>不易消除（还是从消除静态冒险入手）

　　含有静态冒险的卡诺图圈与圈之间相切

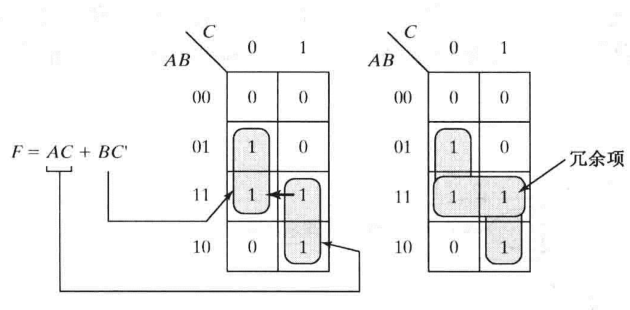
　　静态冒险消除：添加冗余，覆盖冒险

　　步骤：（1）消除f中的静态1冒险，得到f1

　　　　　（2）查找f1中是否有静态0冒险，消除后圈0得到f2'

　　　　　（3）对f2'取反，得到f2既无1态冒险也无0态冒险

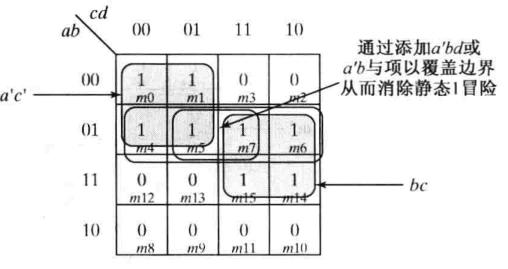
（1）消除静态1冒险

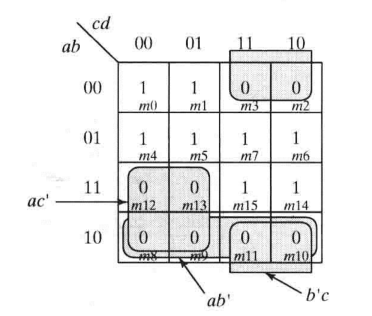
（2）消除静态0冒险

　　（1）F=a'c'+bc画在卡诺图上为两个圈相切且没有联系，含有1态冒险，增加冗余项a'b后消除；得到F1=a'c'+bc+a'b

　　（2）在此基础上，得到F1'，即F1'=(a'+c)(a'+b)(b+c'),但注意到0态冒险已经被覆盖（否则需要额外的圈0，加入或项与F1'相与，并取反得到既无1态又无0态冒险的布尔表达式）

逻辑设计模块

　与非-或非门

　　在CMOS工艺中NAND和NOR门比AND和OR门实现起来更高效。总的来说，非门是最简单的门电路，另一方面可以提高带载能力；与非门和或非门是最常用的且相对简单的；同相门是相对比较复杂的。

　　积之和形式的布尔表达式很容易化成与非门形式表示。如F=AB+BC+CD，可以对表达式连续取两次非，即F=(AB+BC+CD)''，保留一个非，另一个非与括号内的项利用德摩根律得到F=[(AB）'+（BC）'+（CD)']’。

　　和之积形式的布尔表达式也很容易化成或非门表示。

　多路复用器和解复用器

　　多路复用器在数字电路中十分常用。

　　简单来说，多路复用器的功能就是利用select信号选出若干输入信号中的一路信号到输出，所以也叫数据选择器。如下图。

　　

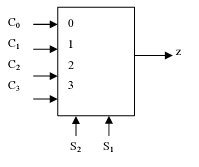
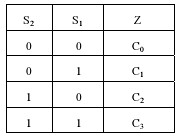
　　多路解复用器与其相反，功能是将一路输入信号选择输出到若干路输出的一路。

　编码器和译码器器

　　编码器是将输入信号转化为对应的二进制数码，用二进制码的形式存储数据。

　　译码器是将二进制码还原成原来信号。

　　编码器有n个输入，m个输出，关系2^m=n，输出位数比输入少。相对应的，译码器的输出位数比输入多。

　　限制：编码器仅允许输入一个位有效

　　优先编码器：允许多个输入同时有效，根据优先权规则形成对应输出，解决了普通编码器的问题。如图。

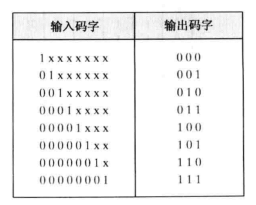
总结

　　本文章针对数字电路中组合逻辑的基础问题进行了总结和分享，文中可能有疏漏和不足，也希望各位看客能够提出宝贵的意见！