p2421 荒岛野人

传送门

题目

克里特岛以野人群居而著称。岛上有排列成环行的M个山洞。这些山洞顺时针编号为1,2,…,M。岛上住着N个野人，一开始依次住在山洞C1,C2,…,CN中，以后每年，第i个野人会沿顺时针向前走Pi个洞住下来。每个野人i有一个寿命值Li，即生存的年数。

下面四幅图描述了一个有6个山洞，住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为1，2，3；每年要走过的洞穴数依次为3，7，2；寿命值依次为4，3，1。

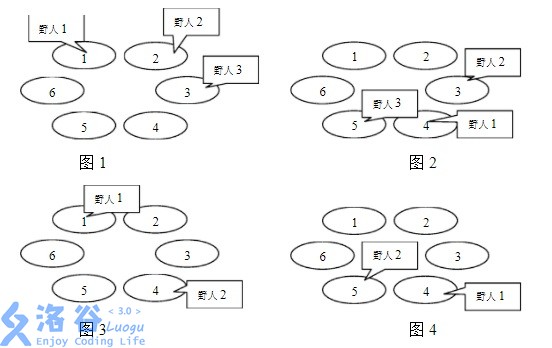
奇怪的是，虽然野人有很多，但没有任何两个野人在有生之年处在同一个山洞中，使得小岛一直保持和平与宁静，这让科学家们很是惊奇。他们想知道，至少有多少个山洞，才能维持岛上的和平呢？

输入格式：

第1行为一个整数N(1<=N<=15)，即野人的数目。

第2行到第N+1每行为三个整数Ci, Pi, Li (1<=Ci,Pi<=100, 0<=Li<=106 )，表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

输出格式：仅包含一个数M，即最少可能的山洞数。输入数据保证有解，且M不大于10^6。

分析

暴力枚举m的大小，然后判断此时每对野人是否会相遇，如果他们永远不会相遇或相遇时间大于两野人中寿命最短的所活时间则不会相遇，具体求解过程同青蛙的约会。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
int c[],p[],l[],n;
inline int gcd(int a,int b){return a%b==?b:gcd(b,a%b);}
inline void exgcd(int a,int b,int &x,int &y){
      if(b==){x=,y=;return;}exgcd(b,a%b,x,y);
      int t=x;x=y;y=t-(a/b)*y;return;
}
inline bool go(int i,int j,int b){
      int a=p[i]-p[j],f=c[j]-c[i],g=gcd(a,b),x,y;
      if(f%g==){
          a/=g,b/=g,f/=g;
          exgcd(a,b,x,y);
          b=abs(b);
          x=(x%b*f%b+b)%b;
          if(x<=min(l[i],l[j]))return ;
      }
      return ;
}
inline bool check(int m){
      int i,j,k;
      for(i=;i<n;i++)
        for(j=i+;j<=n;j++)
          if(!go(i,j,m))return ;
      return ;
}
int main()
{     int m=,i,j,k;
      scanf("%d",&n);
      for(i=;i<=n;i++)scanf("%d%d%d",&c[i],&p[i],&l[i]),m=max(m,c[i]);
      while(m){
          if(check(m)){
            printf("%d\n",m);
            return ;
        }
          m++;
      }
      return ;
}