直接选择排序&堆排序

1.什么是直接选择排序？

　　直接选择排序(Straight Select Sort)是一种简单的排序方法，它的基本思想是：通过n-i次关键字之间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i(1<=i<=n)个记录交换位置。

　　时间复杂度O(n²)

　　在排序时找到合适的关键字再做交换，并且只移动一次。
　　

public class Test1{
	public static void selectSort(int[] arr){
		for(int i=0;i<arr.lenght;i++){
			for(int j=i+1;j<arr.length;j++){
				if(arr[i]>arr[j])//找到后面的元素比前面的小，就交换
				swap(arr,i,j);
			}
		}
	}
	private static void swap(int[] arr,int x,int y){
		int temp=arr[x];
		arr[x]=arr[y];
		arr[y]=temp;
	}
	public static void main(String[] args){
		int[] a={4,2,1,6,0,-5,1};
		int i;
		selectSort(a);
		for(i=0;i<7;i++)
			System.out.print(a[i]);
	}
}

栗子：排序算法中，比较次数与初始序列无关的排序方法有哪些？D

　　A.希尔排序

　　B.快速排序

　　C.堆排序

　　D.选择排序

2.堆排序

　　时间复杂度为O(nlogn),不稳定排序

　　堆是一个完全二叉树，树中每一个结点对应于原始数据的一个记录，并且每个结点应满足以下条件：非叶结点的数据大于或等于其左右孩子结点的数据（大顶堆）

　　若是按从小到大的顺序排序，则要求非叶结点的数据小于或等于其左右孩子结点的数据（小顶堆）

　　由堆的定义可以看出，其根结点为最大值，堆排序就是利用这一特性进行的。

　　堆的存储

　　一般都用数组来表示堆，i 结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

　　关于二叉树的一个性质：

　　如果对于一棵有n个结点的完全二叉树，对于任一结点 i有：

　　（1）如果i=1,则结点 i 是二叉树的根，无双亲;如果i>1,则其双亲是结点 i/2

　　（2）如果 2i>n，则结点 i 无左孩子（结点i是叶子结点），否则其左孩子是结点2i;

　　（3）如果2i+1>n，则结点 i 无右孩子，否则其右孩子是结点2i+1;

　　堆排序的大致过程包括两个阶段：

　　（1）将无序的数据构成堆（即用无序的数据生成满足堆定义的完全二叉树）

　　（2）利用堆排序（即用上一步生成的堆输出有序数据）

　　首先把无序数据构成堆

　　　　

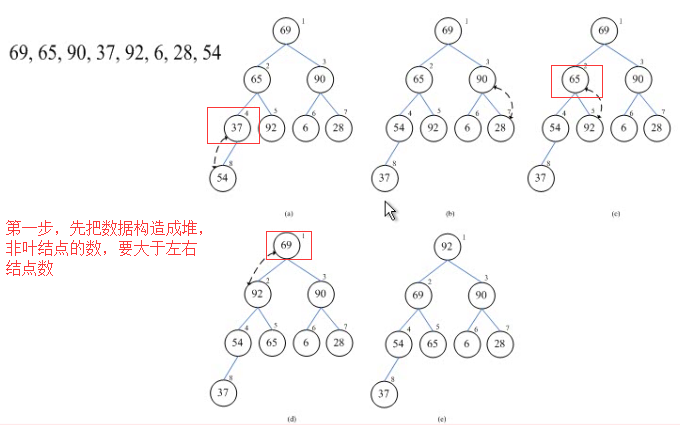
//构成堆
public static void HeapAdjust(int[] a,int s,int n){
	int j,t;
	while(2*s+1<n){//第s个结点有右子树
		j=2*s+1;//左子树
		if((j+1)<n){
			if(a[j]<a[j+1])//如果左子树小于右子树，则需要比较右子树和s结点
			j++;//序号加1，指向右子树
		}
		if(a[s]<a[j]){//如果s结点小于它的右子树，就进行交换
			t=a[s];
			a[s]=a[j];
			a[j]=t;
			s=j;//之前的堆被破坏了，需要调整
		}
		else{//比较左右孩子均大则堆未被破坏，不需要调整
			break;
		}
	}
}

　　

　　然后，每次将最后的数据（37）与最上面的数据（92）交换顺序，然后把把交换后的最上面的数据（92）输出，由于交换后肯定不满足堆了，就再重新构成堆。接下来接着进行交换。

　　

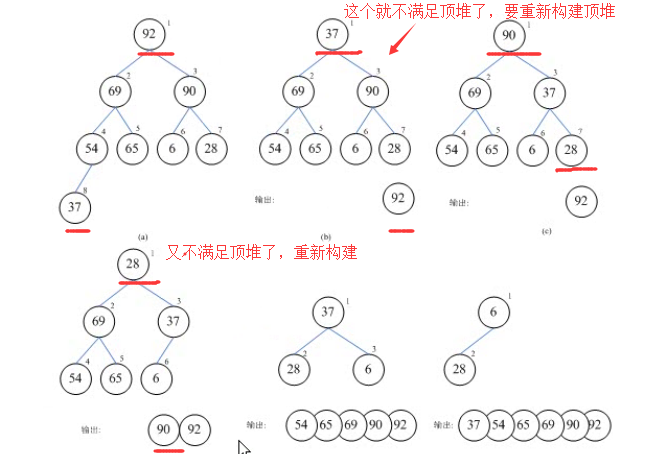
//堆排序
public static void HeapSort(int[] a,int n){
	int t,i;
	int j;
	for(i=n/2-1;i>=0;i--){
		HeapAdjust(a,i,n);//将a[0,n-1]构成大顶堆
	}
	for(i=n-1;i>0;i++){//将最后的一个，与第一个进行比较
		t=a[0];
		a[0]=a[i];
		a[i]=t;
		HeapAdjust(a,0,i);//将a[0]至a[i]重新进行调整
	}
}