manacher求最长回文子串算法

原文：http://www.felix021.com/blog/read.php?2040

首先用一个非常巧妙的方式，将所有可能的奇数/偶数长度的回文子串都转换成了奇数长度：在每个字符的两边都插入一个特殊的符号。比如 abba 变成 #a#b#b#a#， aba变成 #a#b#a#。 为了进一步减少编码的复杂度，可以在字符串的开始加入另一个特殊字符，这样就不用特殊处理越界问题，比如 @#a#b#a#（注意，下面的代码是用C语言写 就，由于C语言规范还要求字符串末尾有一个'\0'所以正好OK，但其他语言可能会导致越界）。

下面以字符串12212321为例，经过上一步，变成了 S[] = "@#1#2#2#1#2#3#2#1#";

然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度（包括S[i]，也就是把该回文串“对折”以后的长度），比如S和P的对应关系：

S  #    #    #    #    #    #    #    #    #
P
(p.s. 可以看出，P[i]-1正好是原字符串中回文串的总长度）

那么怎么计算P[i]呢？该算法增加两个辅助变量（其实一个就够了，两个更清晰）id和mx，其中id表示最大回文子串中心的位置，mx则为id+P[id]，也就是最大回文子串的边界。

然后可以得到一个非常神奇的结论，这个算法的关键点就在这里了：如果mx > i，那么P[i] >= MIN(P[2 * id - i], mx - i)。就是这个串卡了我非常久。实际上如果把它写得复杂一点，理解起来会简单很多：

//记j = 2 * id - i，也就是说 j 是 i 关于 id 的对称点。
if (mx - i > P[j])
    P[i] = P[j];
else /* P[j] >= mx - i */
    P[i] = mx - i; // P[i] >= mx - i，取最小值，之后再匹配更新。

当然光看代码还是不够清晰，还是借助图来理解比较容易。

当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。

当
P[j] >= mx - i
的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是
说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx -
i。至于mx之后的部分是否对称，就只能老老实实去匹配了。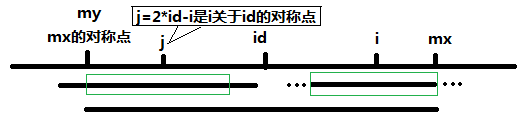

对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了。

于是代码如下：

//输入，并处理得到字符串s
int p[], mx = , id = ;
memset(p, , sizeof(p));
for (i = ; s[i] != '\0'; i++) {
    p[i] = mx > i ? min(p[*id-i], mx-i) : ;
    while (s[i + p[i]] == s[i - p[i]]) p[i]++;
    if (i + p[i] > mx) {
        mx = i + p[i];
        id = i;
    }
}
//找出p[i]中最大的