PCB genesis Slot槽转钻孔(不用G85命令)实现方法

PCB钻Slot槽一般都采用G85命令钻槽孔,而采用G85命令工程CAM无法准确的知道Slot槽钻多少个孔,并不能决定钻槽孔的顺序,因为采用G85命令钻孔密度与钻槽顺序由钻机本身决定的.在这里介绍一种如果不用G85命令,如何将Slot槽生成多个钻孔。

一.我们先了解一下G85命令钻槽

钻孔顺序

孔密度

连一篇文章有关于Slot槽孔数计算方式： https://www.cnblogs.com/pcbren/p/9379178.html

二.求解思路

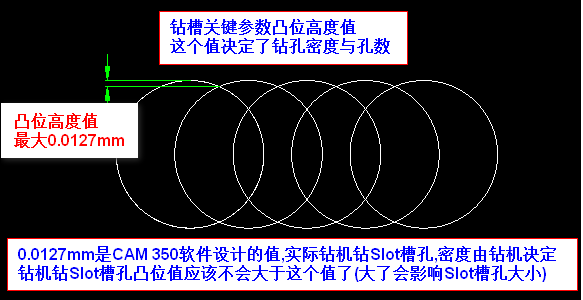
1.通过孔密度,求出孔与孔中心距离

2.再以Slot槽的一端做为起点，增量值(孔中心距)，方位角(Slot槽的方位角)，逐个求出下一个钻孔位置.直到到达Slot槽终点节止。

三.C#简易代码实现:

1.Slot槽转钻孔代码(这里段代码实现将Slot槽转为钻孔,钻孔顺序是一个SLOT槽依次逐个从头钻到头尾,和G85命令钻槽顺序不一样)

            string drilllayer = "drl";
            gLayer layer = g.getFEATURES($"{drilllayer}", g.STEP, g.JOB, "mm", true);
            List<gPP> pList = new List<gPP>();
            foreach (var line in layer.Llist)
            {
                var HoleCenterDi = calc2.p_Convex(line.width * 0.0005);
                pList.AddRange(calc2.l_2Plist(line, HoleCenterDi, true));
            }
            foreach (var arc in layer.Alist)
            {
                var HoleCenterDi = calc2.p_Convex(arc.width * 0.0005);
                pList.AddRange(calc2.a_2Plist(arc, HoleCenterDi,, true));
            }
            addCOM.pad(pList);

2.计算函数

        /// <summary>
        /// 通过孔半径与凸高位求  孔中心距
        /// </summary>
        /// <param name="Rradius">孔半径</param>
        /// <param name="tol_">凸位高度值</param>
        /// <returns></returns>
        public double p_Convex(double Rradius, double tol_ = 0.0127)
        {
            return Math.Sqrt(Math.Pow(Rradius, ) - Math.Pow(Rradius - tol_, )) * ;
        }
        /// <summary>
        /// 线Line 转点P组集
        /// </summary>
        /// <param name="l"></param>
        /// <param name="len_">点的间距</param>
        /// <returns></returns>
        public List<gPP> l_2Plist(gL l, double len_ = 0.1d, bool is_avg = false)
        {
            List<gPP> list_point = new List<gPP>();//采用优先占用线两端  如果有从线的一端出发增量间距后续再做更改
            double line_len = l_Length(l);
            gPP tempP;
            tempP.p = l.ps;
            tempP.symbols = l.symbols;
            tempP.width = l.width;
            list_point.Add(tempP);
            int avg_count = (int)(Math.Ceiling(line_len / len_)) - ;
            if (avg_count > )
            {
                if (is_avg)
                    len_ = line_len / avg_count;
                double angle_ = p_ang(l.ps, l.pe);
                for (int i = ; i < avg_count; i++)
                {
                    tempP = p_val_ang(tempP, len_, angle_);
                    list_point.Add(tempP);
                }
            }
            tempP.p = l.pe;
            list_point.Add(tempP);
            return list_point;
        }
        /// <summary>
        /// 求方位角
        /// </summary>
        /// <param name="ps"></param>
        /// <param name="pe"></param>
        /// <returns></returns>
        public double p_ang(gPoint ps, gPoint pe)
        {
            double a_ang = Math.Atan((pe.y - ps.y) / (pe.x - ps.x)) / Math.PI * ;
            //象限角  转方位角   计算所属象限   并求得方位角
            if (pe.x >= ps.x && pe.y >= ps.y)  //↗    第一象限
            {
                return a_ang;
            }
            else if (!(pe.x >= ps.x) && pe.y >= ps.y)  // ↖   第二象限
            {
                return a_ang + ;
            }
            else if (!(pe.x >= ps.x) && !(pe.y >= ps.y))  //↙   第三象限
            {
                return a_ang + ;
            }
            else if (pe.x >= ps.x && !(pe.y >= ps.y))  // ↘   第四象限
            {
                return a_ang + ;
            }
            else
            {
                return a_ang;
            }
        }//求方位角
        /// <summary>
        /// 求增量坐标
        /// </summary>
        /// <param name="ps">起点</param>
        /// <param name="val">增量值</param>
        /// <param name="ang_direction">角度</param>
        /// <returns></returns>
        public gPP p_val_ang(gPP ps, double val, double ang_direction)
        {
            gPP pe = ps;
            pe.p.x = ps.p.x + val * Math.Cos(ang_direction * Math.PI / );
            pe.p.y = ps.p.y + val * Math.Sin(ang_direction * Math.PI / );
            return pe;
        }
        /// <summary>
        /// 求线Line长度
        /// </summary>
        /// <param name="l"></param>
        /// <param name="is_calc_width"></param>
        /// <returns></returns>
        public double l_Length(gL l, bool is_calc_width = false)
        {
            if (is_calc_width)
                return Math.Sqrt((l.ps.x - l.pe.x) * (l.ps.x - l.pe.x) + (l.ps.y - l.pe.y) * (l.ps.y - l.pe.y)) + l.width / ;
            else
                return Math.Sqrt((l.ps.x - l.pe.x) * (l.ps.x - l.pe.x) + (l.ps.y - l.pe.y) * (l.ps.y - l.pe.y));
        }
        /// <summary>
        /// 弧Arc 转点P组集
        /// </summary>
        /// <param name="a"></param>
        /// <param name="val_">此数值表示:分段数值</param>
        /// <param name="type_">代表值数值类型 【0】弧长 【1】角度  【2】弦长 </param>
        /// <param name="is_avg">是否平均分布 </param>
        /// <returns></returns>
        public List<gPP> a_2Plist(gA a, double val_ = 0.1d, int type_ = , bool is_avg = false)
        {
            List<gPP> list_point = new List<gPP>();
            gPP tempP;
            tempP.p = a.ps;
            tempP.symbols = a.symbols;
            tempP.width = a.width;
            list_point.Add(tempP);

            double avg_count;
            double angle_val = ;
            double rad_ = p2p_di(a.pc, a.pe);
            double sum_alge = a_Angle(a);
            if (type_ == )  //    【1】角度
            {
                angle_val = val_;
                avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - ;  //  总角度/单角度
            }
            else if (type_ == )  //【2】弦长
            {
                angle_val = Math.Asin(val_ / (rad_ * )) *  / pi;
                avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - ;  //  总角度/单角度
            }
            else  //                【0】弧长
            {
                angle_val = val_ *  / (pi * rad_);
                avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - ;  //  总角度/单角度
                //avg_count = (int)(Math.Ceiling(a_Lenght(a) / val_)) - 1;  //  或  总弧长/单弧长
            }
            if (is_avg)
                angle_val = sum_alge / avg_count;
            if (avg_count > )
            {
                gPP centerP = tempP;
                centerP.p = a.pc;
                double angle_s = p_ang(a.pc, a.ps);
                if (a.ccw) { angle_val =  - angle_val; }
                for (int i = ; i < avg_count; i++)
                {
                    tempP = p_val_ang(centerP, rad_, angle_s - angle_val * i);
                    list_point.Add(tempP);
                }
            }
            if (!(zero(a.ps.x - a.pe.x) && zero(a.ps.y - a.pe.y)))
            {
                tempP.p = a.pe;
                list_point.Add(tempP);
            }
            return list_point;
        }
        /// <summary>
        /// 返回两点之间欧氏距离
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <returns></returns>
        public double p2p_di(gPoint p1, gPoint p2)
        {
            return Math.Sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
        }
        /// <summary>
        /// 求弧Arc圆心角       //后续改进  用叉积 与3P求角度求解  验证哪个效率高
        /// </summary>
        /// <param name="a"></param>
        /// <returns></returns>
        public double a_Angle(gA a)
        {
            double angle_s, angle_e, angle_sum;
            if (a.ccw)
            {
                angle_s = p_ang(a.pc, a.pe);
                angle_e = p_ang(a.pc, a.ps);
            }
            else
            {
                angle_s = p_ang(a.pc, a.ps);
                angle_e = p_ang(a.pc, a.pe);
            }
            if (angle_s == ) { angle_s = ; }
            if (angle_e >= angle_s)
                angle_sum =  - Math.Abs(angle_s - angle_e);
            else
                angle_sum = Math.Abs(angle_s - angle_e);
            return angle_sum;
        }

3.Point,PAD,Line,Arc数据结构

    /// <summary>
    /// 精简 PAD  数据类型
    /// </summary>
    public struct gPP
    {
        public gPP(double x_val, double y_val, double width_)
        {
            this.p = new gPoint(x_val, y_val);
            this.symbols = "r";
            this.width = width_;
        }
        public gPP(gPoint p_, double width_)
        {
            this.p = p_;
            this.symbols = "r";
            this.width = width_;
        }
        public gPP(gPoint p_, string symbols_, double width_)
        {
            this.p = p_;
            this.symbols = symbols_;
            this.width = width_;
        }
        public gPoint p;
        public string symbols;
        public double width;
        public static gPP operator +(gPP p1, gPP p2)
        {
            p1.p += p2.p;
            return p1;
        }
        public static gPP operator +(gPP p1, gPoint p2)
        {
            p1.p += p2;
            return p1;
        }
        public static gPP operator -(gPP p1, gPP p2)
        {
            p1.p -= p2.p;
            return p1;
        }
        public static gPP operator -(gPP p1, gPoint p2)
        {
            p1.p -= p2;
            return p1;
        }
    }
    /// <summary>
    /// 点  数据类型 (XY)
    /// </summary>
    public struct gPoint
    {
        public gPoint(gPoint p_)
        {
            this.x = p_.x;
            this.y = p_.y;
        }
        public gPoint(double x_val, double y_val)
        {
            this.x = x_val;
            this.y = y_val;
        }
        public double x;
        public double y;
        public static gPoint operator +(gPoint p1, gPoint p2)
        {
            p1.x += p2.x;
            p1.y += p2.y;
            return p1;
        }
        public static gPoint operator -(gPoint p1, gPoint p2)
        {
            p1.x -= p2.x;
            p1.y -= p2.y;
            return p1;
        }
    }
    /// <summary>
    /// Line 数据类型
    /// </summary>
    public struct gL
    {
        public gL(double ps_x, double ps_y, double pe_x, double pe_y, double width_)
        {
            this.ps = new gPoint(ps_x, ps_y);
            this.pe = new gPoint(pe_x, pe_y);
            this.negative = false;
            this.symbols = "r";
            this.attribut = string.Empty;
            this.width = width_;
        }
        public gL(gPoint ps_, gPoint pe_, double width_)
        {
            this.ps = ps_;
            this.pe = pe_;
            this.negative = false;
            this.symbols = "r";
            this.attribut = string.Empty;
            this.width = width_;
        }
        public gL(gPoint ps_, gPoint pe_, string symbols_, double width_)
        {
            this.ps = ps_;
            this.pe = pe_;
            this.negative = false;
            this.symbols = symbols_;
            this.attribut = string.Empty;
            this.width = width_;
        }
        public gPoint ps;
        public gPoint pe;
        public bool negative;//polarity-- positive  negative
        public string symbols;
        public string attribut;
        public double width;
        public static gL operator +(gL l1, gPoint move_p)
        {
            l1.ps += move_p;
            l1.pe += move_p;
            return l1;
        }
        public static gL operator +(gL l1, gP move_p)
        {
            l1.ps += move_p.p;
            l1.pe += move_p.p;
            return l1;
        }
        public static gL operator -(gL l1, gPoint move_p)
        {
            l1.ps -= move_p;
            l1.pe -= move_p;
            return l1;
        }
        public static gL operator -(gL l1, gP move_p)
        {
            l1.ps -= move_p.p;
            l1.pe -= move_p.p;
            return l1;
        }
    }
    /// <summary>
    /// ARC 数据类型
    /// </summary>
    public struct gA
    {
        public gA(double ps_x, double ps_y, double pc_x, double pc_y, double pe_x, double pe_y, double width_, bool ccw_)
        {
            this.ps = new gPoint(ps_x, ps_y);
            this.pc = new gPoint(pc_x, pc_y);
            this.pe = new gPoint(pe_x, pe_y);
            this.negative = false;
            this.ccw = ccw_;
            this.symbols = "r";
            this.attribut = string.Empty;
            this.width = width_;
        }
        public gA(gPoint ps_, gPoint pc_, gPoint pe_, double width_, bool ccw_ = false)
        {
            this.ps = ps_;
            this.pc = pc_;
            this.pe = pe_;
            this.negative = false;
            this.ccw = ccw_;
            this.symbols = "r";
            this.attribut = string.Empty;
            this.width = width_;
        }
        public gPoint ps;
        public gPoint pe;
        public gPoint pc;
        public bool negative;//polarity-- positive  negative
        public bool ccw; //direction-- cw ccw
        public string symbols;
        public string attribut;
        public double width;
        public static gA operator +(gA arc1, gPoint move_p)
        {
            arc1.ps += move_p;
            arc1.pe += move_p;
            arc1.pc += move_p;
            return arc1;
        }
        public static gA operator +(gA arc1, gP move_p)
        {
            arc1.ps += move_p.p;
            arc1.pe += move_p.p;
            arc1.pc += move_p.p;
            return arc1;
        }
        public static gA operator -(gA arc1, gPoint move_p)
        {
            arc1.ps -= move_p;
            arc1.pe -= move_p;
            arc1.pc -= move_p;
            return arc1;
        }
        public static gA operator -(gA arc1, gP move_p)
        {
            arc1.ps -= move_p.p;
            arc1.pe -= move_p.p;
            arc1.pc -= move_p.p;
            return arc1;
        }
    }

四.实现效果