【HIHOCODER 1163】 博弈游戏·Nim游戏

描述

---

今天我们要认识一对新朋友，Alice与Bob。

Alice与Bob总是在进行各种各样的比试，今天他们在玩一个取石子的游戏。

在这个游戏中，Alice和Bob放置了N堆不同的石子，编号1..N，第i堆中有A[i]个石子。

每一次行动，Alice和Bob可以选择从一堆石子中取出任意数量的石子。至少取1颗，至多取出这一堆剩下的所有石子。

Alice和Bob轮流行动，取走最后一个石子的人获得胜利。

假设每一轮游戏都是Alice先行动，请你判断在给定的情况下，如果双方都足够聪明，谁会获得胜利？

输入

---

第1行：1个整数N。表示石子堆数。1≤N≤100

第2行：N个整数，第i个整数表示第i堆石子的个数A[i]，1≤A[i]≤10000

输出

---

第1行：1个字符串，若Alice能够获胜输出"Alice"，否则输出"Bob"

样例输入

3
3 2 1

样例输出

Bob

题解

提示给出的证明很妙

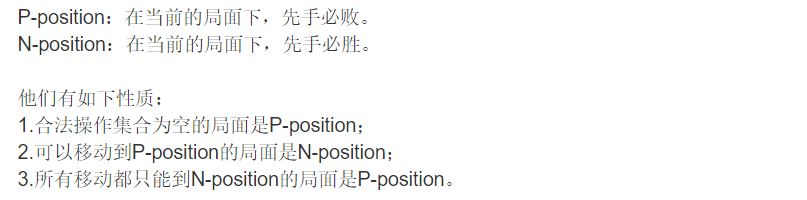
参考代码

import java.io.*;
import java.util.*;
public class Main {
	static final int N=30005;
	static final int inf=0x3f3f3f3f;
	public static void main(String[] args) {
        InputStream sys=System.in;
        InputReader in=new InputReader(sys);
        PrintWriter out=new PrintWriter(System.out);
        int n=in.nextInt(),ans=0;
        for(int i=1;i<=n;i++) {
        	ans^=in.nextInt();
        }
        out.println(ans==0?"Bob":"Alice");
        out.flush();
    }
	static class InputReader {
		public BufferedReader reader;
		public StringTokenizer tokenizer;
		public InputReader(InputStream stream) {
			reader = new BufferedReader(new InputStreamReader(stream), 32768);
			tokenizer = null;
		}
		public String next() {
			while (tokenizer == null || !tokenizer.hasMoreTokens()) {
				try {
					tokenizer = new StringTokenizer(reader.readLine());
				} catch (IOException e) {
					throw new RuntimeException(e);
				}
			}
			return tokenizer.nextToken();
		}
		public int nextInt() {
			return Integer.parseInt(next());
		}
		public long nextLong() {
			return Long.parseLong(next());
		}
		public double nextDouble() {
			return Double.parseDouble(next());
		}
	}
}