luogu P3371 & P4779 单源最短路径spfa & 最大堆优化Dijkstra算法

P3371 【模板】单源最短路径（弱化版）

题目背景

本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过，如有需要请移步 P4779。

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15；

对于40%的数据：N<=100，M<=10000；

对于70%的数据：N<=1000，M<=100000；

对于100%的数据：N<=10000，M<=500000。保证数据随机。

对于真正 100% 的数据，请移步 P4779。请注意，该题与本题数据范围略有不同。

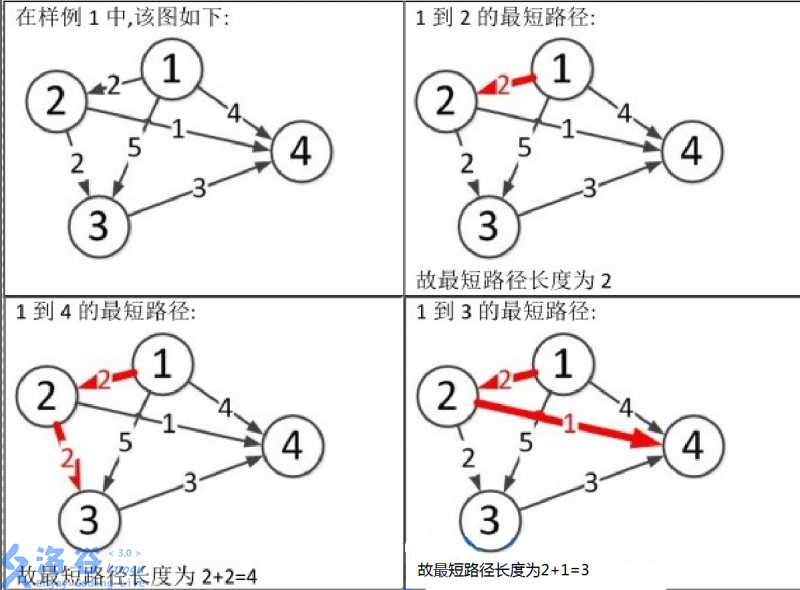
样例说明：图片1到3和1到4的文字位置调换

解题思路：spfa算法是Bellman-Ford算法的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。spfa最坏情况下复杂度和朴素Bellman-Ford一样为O(|V||E|)。在非负边权图中为了避免出现最坏情况，通常使用效率更加稳定的Dijkstra算法，以及它的堆优化版本。数据较水，直接拿spfa板子水过。spfa思想：每次只需对上一次更新过的点的邻接点进行更新即可，因为上一次更新的点只对其未更新的邻接点有影响，所以无需像bellman-ford算法一样盲目遍历每条边。另外，出队的顶点要标记为false，即出队的那些点仍有可能对前面已更新过的点到源点的距离再进行更新，同时也要保证每个顶点至多在队列中出现1次，避免浪费时间去重复更新。

AC代码：

 #include<bits/stdc++.h>

 using namespace std;

 typedef long long LL;

 const int maxn=1e5+;

 const int inf=0x3f3f3f3f;

 queue<int> que;vector<int> v1[maxn],v2[maxn];int n,m,s,u,v,w,x,y,z,dis[maxn];bool vis[maxn];

 void spfa(int s){

     while(!que.empty())que.pop();

     que.push(s),vis[s]=true,dis[s]=;

     while(!que.empty()){

         x=que.front();que.pop(),vis[x]=false;//出队则标记不在队列中

         for(size_t j=;j<v1[x].size();++j){

             y=v1[x][j],z=v2[x][j];

             if(dis[x]+z<dis[y]){

                 dis[y]=dis[x]+z;

                 if(!vis[y])que.push(y),vis[y]=true;//标记在队列中

             }

         }

     }

 }

 int main(){

     while(cin>>n>>m>>s){

         for(int i=;i<=n;++i)v1[i].clear(),v2[i].clear();

         memset(vis,false,sizeof(vis));

         while(m--){

             cin>>u>>v>>w;

             v1[u].push_back(v);//邻接点

             v2[u].push_back(w);//对应边权

         }

         memset(dis,0x3f,sizeof(dis));

         spfa(s);

         for(int i=;i<=n;++i)cout<<(dis[i]==inf?:dis[i])<<(i==n?'\n':' ');

     }

     return ;

 }

P4779 【模板】单源最短路径（标准版）

题目背景

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程一题里非常熟练地使用了一个广为人知的算法求最短路。

然后呢？

100→60；

Ag→Cu；

最终，他因此没能与理想的大学达成契约。

小 F 衷心祝愿大家不再重蹈覆辙。

题目描述

给定一个 N 个点，M条有向边的带非负权图，请你计算从S出发，到每个点的距离。

数据保证你能从S出发到任意点。

输入格式：

第一行为三个正整数 N, M, S。第二行起 M 行，每行三个非负整数 $u_i$, $v_i$, $w_i$，表示从 $u_i$ 到 $v_i$ 有一条权值为 $w_i$ 的边。

输出格式：

输出一行N个空格分隔的非负整数，表示S到每个点的距离。

输入样例#1：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：

0 2 4 3
说明
样例解释请参考数据随机的模板题。

1≤N≤100000；

1≤M≤200000；

S=1；

1≤ui,vi≤N；

0≤wi≤10^9,

0≤∑wi≤10^9。

本题数据可能会持续更新，但不会重测，望周知。

2018.09.04 数据更新 from @zzq

解题思路：堆优化Dijkstra算法，其实就是降低了每次去查找当前dis数组中最小值的时间，时间复杂度由原来的O(|V|²)降为O(|E|log|V|)。对于此题，spfa已死，T到爆！

AC代码：

 #include<bits/stdc++.h>

 using namespace std;

 const int maxn=1e5+;

 int n,m,s,u,v,w,x,y,z,dis[maxn];vector<int> v1[maxn],v2[maxn];bool vis[maxn];

 priority_queue< pair<int,int> > que;//最大堆优先队列

 void Dijkstra(){

     while(!que.empty())que.pop();

     memset(vis,false,sizeof(vis));

     dis[s]=;que.push(make_pair(-dis[s],s));//加上负号实现最大堆，便于取出最短路径

     while(!que.empty()){

         x=que.top().second;que.pop();

         if(vis[x])continue;//过滤掉已归纳到最短距离集合的点

         vis[x]=true;//归纳该点到最短路径的集合

         for(size_t j=;j<v1[x].size();++j){//松弛

             y=v1[x][j],z=v2[x][j];

             if(!vis[y]&&(dis[x]+z<dis[y]))dis[y]=dis[x]+z,que.push(make_pair(-dis[y],y));

         }

     }

 }

 int main(){

     while(~scanf("%d%d%d",&n,&m,&s)){

         for(int i=;i<=n;++i)v1[i].clear(),v2[i].clear();

         for(int i=;i<=n;++i)dis[i]=2e9;

         while(m--){

             scanf("%d%d%d",&u,&v,&w);

             v1[u].push_back(v);//邻接点

             v2[u].push_back(w);//边权

         }

         Dijkstra();

         for(int i=;i<=n;++i)printf("%d%c",dis[i],i==n?'\n':' ');

     }

     return ;

 }