ACM_三元一次函数解法（克莱姆法则）

三元一次函数

Time Limit: 2000/1000ms (Java/Others)

Problem Description:

计算三元一次函数。。如图

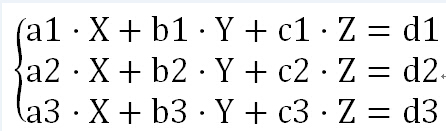
Input:

EOF，先输入n,表示样例个数，输入a1,b1,c1,d1,a2,b2,c2,d2,a3,b3,c3,d3（0=<x,y,z<=1000）

Output:

输出x,y,z(结果保留两位小数)

Sample Input:

2
3 3 1 20.00
6 0 2 20.00
6 4 0 20.00
3 0 1 6.00
0 2 2 10.00
1 3 1 10.00

Sample Output:

1.11 3.33 6.67
1.00 2.00 3.00
解题思路：克莱姆法则。
AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 int main(){
     double a1,b1,c1,d1,a2,b2,c2,d2,a3,b3,c3,d3,D,D1,D2,D3;int t;
     while(cin>>t){
         while(t--){
             cin>>a1>>b1>>c1>>d1>>a2>>b2>>c2>>d2>>a3>>b3>>c3>>d3;
             D  = a1*(b2*c3 - b3*c2) - a2*(b1*c3 - b3*c1) + a3*(b1*c2 - b2*c1);
             D1 = d1*(b2*c3 - b3*c2) - d2*(b1*c3 - b3*c1) + d3*(b1*c2 - b2*c1);
             D2 = a1*(d2*c3 - d3*c2) - a2*(d1*c3 - d3*c1) + a3*(d1*c2 - d2*c1);
             D3 = a1*(b2*d3 - b3*d2) - a2*(b1*d3 - b3*d1) + a3*(b1*d2 - b2*d1);
             printf("%.2f %.2f %.2f\n",D1/D,D2/D,D3/D);
         }
     }
     return ;
 }

废寝忘食的大牛

Time Limit: 2000/1000ms (Java/Others)

Problem Description:

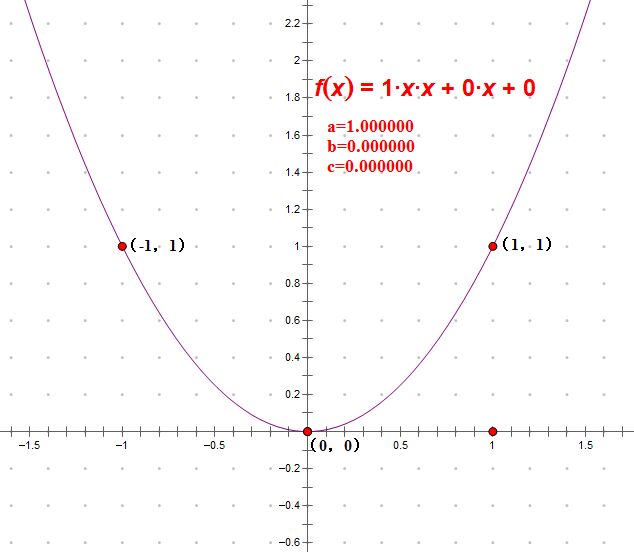
某大牛最近废寝忘食地打代码，整天泡网吧（总觉得除了打代码还干了别的事情？），可就是这么励志的一个奋斗的大好青年，每次打完比赛都听不到题解，愤怒啊有木有，悲怆啊有木有，为了报复社会（？），他召唤了（shenmegui）一只还在读初中的小妹妹出了道题，恰好这小妹妹最近刚学了抛物线（y=ax^2+bx+c），那么问题就来了，挖掘机技术到底哪家强（误），额，不，是给出三个不重叠的点的坐标，求抛物线的表达式。

Input:

输入有多组测试数据，每组测试数据包括三个点的坐标，坐标点为整数，x1，y1，x2，y2，x3，y3，（-5000<xi，yi<5000）。

Output:

对于每组测试数据，请分别输出抛物线表达式的a,b,c值（保留六位小数）。若不构成抛物线，那就输出SB。因为小妹妹觉得这是道简单的题目。

Sample Input:

-1 1 0 0 1 1

Sample Output:

a=1.000000,b=0.000000,c=0.000000.
解题思路：克莱姆法则求抛物线的系数。
AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 int main(){
     LL a1,b1,a2,b2,a3,b3,D,D1,D2,D3;//要用long long，避免数据溢出
     while(cin>>a1>>b1>>a2>>b2>>a3>>b3){
         D  = a1*a1*(a2-a3) - a2*a2*(a1-a3) + a3*a3*(a1-a2);
         D1 = b1*(a2-a3) - b2*(a1-a3) + b3*(a1-a2);
         D2 = a1*a1*(b2-b3) - a2*a2*(b1-b3) + a3*a3*(b1-b2);
         D3 = a1*a1*(a2*b3-a3*b2) - a2*a2*(a1*b3-a3*b1) + a3*a3*(a1*b2-a2*b1);
         if(!D||!D1)puts("SB");//无解SB
         else printf("a=%.6f,b=%.6f,c=%.6f.\n",1.0*D1/D,!D2?0.0:(1.0*D2/D),!D3?0.0:(1.0*D3/D));
     }
     return ;
 }