单源最短路：Dijkstra算法 及 关于负权的讨论

描述：

对于图（有向无向都适用），求某一点到其他任一点的最短路径（不能有负权边）。

操作：

1. 初始化：

一个节点大小的数组dist[n]

源点的距离初始化为0，与源点直接相连的初始化为其权重，其他为无穷大（INT32_MAX等）。

标记源点，其到自身距离是0，已经是最小了。

2. 计算

对于dist，每次选取未标记的最小值（将其标记，表示已经得到最小值），更新与其相连的未标记的点：

　　如果此点加上权值，小于与其相连的点，则更新之。

代码：

代码并未优化，理解思路即可。

#include <string>
#include <iostream>
#include <vector>
using namespace std;

void Dijkstra() {
    int source = ;  // starting point
    int vex, edge;
    cout << "Input the number of vertexs and edges:" << endl;
    cin >> vex >> edge;
    vector<vector<int> > g = vector<vector<int> >(vex, vector<int>(vex));  // 用二维矩阵储存

    int start, end, weight;
    while(cin >> start >> end >> weight)
        g[start][end] = weight;

    vector<int> res(vex, INT32_MAX);
    vector<bool> visit(vex, false);

    res[source] = ;
    visit[source] = true;

　　 // 初始化
    for (int i = ; i < vex; ++i)
        if (i != source && g[source][i] != )
            res[i] = g[source][i];

　　 // 两层for循环
    for (int i = ; i < vex; ++i) {
        int min_element = INT32_MAX;
        int min_index = -;
　　　　　// 找出最小点
        for (int j = ; j < vex; ++j) {
            if (!visit[j] && res[j] < min_element) {
                min_index = j;
                min_element = res[j];
            }
        }
        if (min_element == INT32_MAX || min_index == -)
            break;

　　　　  // 更新与其直接相连的所有点
        for (int j = ; j < vex; ++j)
            if (g[min_index][j] !=  &&
                  g[min_index][j] + res[min_index] < res[j] &&
　　　　　　　　　　 !visit[j]) {
                res[j] = g[min_index][j] + res[min_index];
                visit[min_index] = true;
            }
    }

    for (int i = ; i < vex; ++i)
        cout << res[i] << endl;
}

证明：

一。第一次选择：

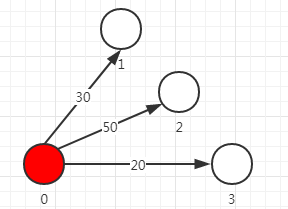
初始数组是0, 30, 50, 20, 其他是无穷大。

此时选择点3，标记，由于其他出路都大于20，不存在任一条路能更快到达3。

二。任一次选择：

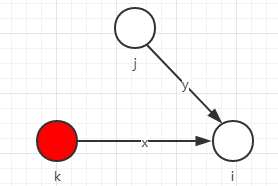
设我们选择了与k相连的i点，将其标记。

需要证明不存在未标记的点j，使得存在一条路径更快到达i点。

不可能的存在，因为如果存在则不可能标记 i，源点到达 j 的距离比到 i 距离近，而 j 前面必定存在被标记的一点s（至少是源点），至少从s开始标记。

证毕。（严格的推导可以设具体变量证明）

关于负权的讨论：

要区分负权边和负权环的概念。

负权边：权重为负数的边。

负权环：源点能到达的一个环，环上权重和为负数。

Dijkstra算法不能包含负权边，含有负权环可以用bellman-ford算法计算。

即使不是负权环，Dijkstra也不能算，如果加入负边，上面证明就不成立。

负权环不存在最短路！

关于Dijkstra算法不能计算负权边：

不是说对于所有含有负权的图都不能计算，如下可以计算：

当负权边指向一个有唯一入边的情况：

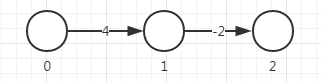
碰巧：

还有其他情况。所以，如果含有负权边使用Dijkstra算法，可能对可能错。

有些不能计算：

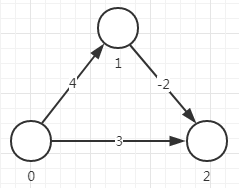
这种情况，第一次会选择 点2，标记最短路径为3，实际最短是0->1->2，距离为2。

复杂度：

用邻接矩阵储存的图：

复杂度为O(V^2 + E)，但E最大也不过V^2，也可以表示为O(V^2)。

原因：外层for循环，O(V)。内层，查找最小点O(V)，更新这点的每条边e，

则：V(V + e) => V^2 + Ve，总共E条边，即V^2 + E。邻接表也一样。

用二叉堆维护最短距离数组：

复杂度为O((V + E)logV)。

原因：外层仍然是V。内层，取出最小值logV，更新点的e条边，且需要入堆，则为elogV，

则：V(logV + elogV) => VlogV + VelogV => VlogV + ElogV => (V + E)logV。

关键在于堆本来是空的，每次更新，都将其入堆，然后从堆中选出最小的，将其标记，可以参考其实现代码理解。

用斐波那契堆维护的最短距离数组：

复杂度：O(VlogV + E)

查下这种堆各操作复杂度即可知道，入堆为O(1)，弹出为O(logN)，则同上：

V(logV + e)，即VlogV + E。