Classification week2: logistic regression classifier 笔记
华盛顿大学 machine learning: Classification 笔记。
linear classifier 线性分类器

多项式:

Logistic regression & 概率模型

P(y = +1 | x) = ?
使用 logistic函数

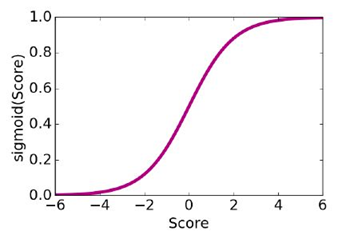
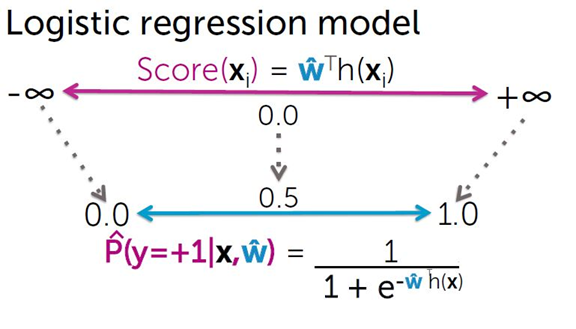
这个概率模型怎么来的?
(李航《统计学习方法》)

即
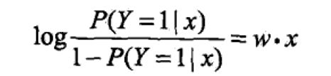
考虑对输入x进行分类的线性函数 w x,其值域为实数域,线性函数wx可转换为概率:
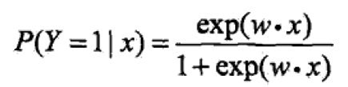
这时,线性函数值越接近正无穷,概率值就越接近1;线性函数值越接近负无穷,
概率值就越接近0。
这种概率描述适用于这样的情况:即在P=0或P=1附近,P对X的变化不敏感。这种概率模型的应用场景主要是分类。
极大似然估计模型参数w
Maximize Likelihood Estimation(MLE) 极大似然估计

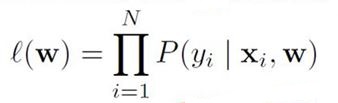
即 选择使 l(w) 最大的参数 w。
对 l(w) 取对数:

展开得
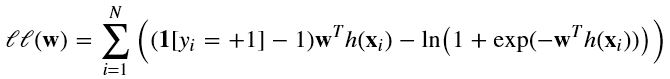
梯度下降(Gradient-descent):

防止过拟合:

即
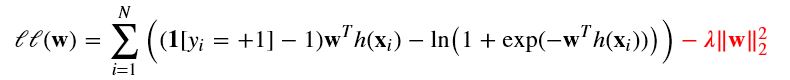
梯度下降
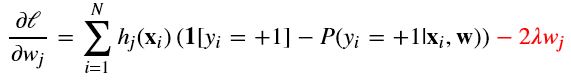
Classification week2: logistic regression classifier 笔记的更多相关文章
- 学习Logistic Regression的笔记与理解(转)
学习Logistic Regression的笔记与理解 1.首先从结果往前来看下how logistic regression make predictions. 设我们某个测试数据为X(x0,x1, ...
- 李宏毅机器学习笔记3:Classification、Logistic Regression
李宏毅老师的机器学习课程和吴恩达老师的机器学习课程都是都是ML和DL非常好的入门资料,在YouTube.网易云课堂.B站都能观看到相应的课程视频,接下来这一系列的博客我都将记录老师上课的笔记以及自己对 ...
- Classification and logistic regression
logistic 回归 1.问题: 在上面讨论回归问题时.讨论的结果都是连续类型.但假设要求做分类呢?即讨论结果为离散型的值. 2.解答: 假设: 当中: g(z)的图形例如以下: 由此可知:当hθ( ...
- 机器学习算法笔记1_2:分类和逻辑回归(Classification and Logistic regression)
形式: 採用sigmoid函数: g(z)=11+e−z 其导数为g′(z)=(1−g(z))g(z) 如果: 即: 若有m个样本,则似然函数形式是: 对数形式: 採用梯度上升法求其最大值 求导: 更 ...
- 分类和逻辑回归(Classification and logistic regression)
分类问题和线性回归问题问题很像,只是在分类问题中,我们预测的y值包含在一个小的离散数据集里.首先,认识一下二元分类(binary classification),在二元分类中,y的取值只能是0和1.例 ...
- Logistic Regression学习笔记
1.李航<统计学习方法>: 2.https://blog.csdn.net/laobai1015/article/details/78113214 3.http://www.cnblogs ...
- 机器学习技法笔记:05 Kernel Logistic Regression
Roadmap Soft-Margin SVM as Regularized Model SVM versus Logistic Regression SVM for Soft Binary Clas ...
- Logistic Regression Using Gradient Descent -- Binary Classification 代码实现
1. 原理 Cost function Theta 2. Python # -*- coding:utf8 -*- import numpy as np import matplotlib.pyplo ...
- 深度学习 Deep LearningUFLDL 最新Tutorial 学习笔记 2:Logistic Regression
1 Logistic Regression 简述 Linear Regression 研究连续量的变化情况,而Logistic Regression则研究离散量的情况.简单地说就是对于推断一个训练样本 ...
随机推荐
- iOS:APNS推送主要代码
首先,在AppDelegate.m 中: 1,注册通知 //[objc] view plaincopyprint?在CODE上查看代码片派生到我的代码片 - (BOOL)application:(UI ...
- 增强学习--Q-leraning
Q-learning 实例代码 import numpy as np import random from environment import Env from collections import ...
- 【angularJS】三个学习angulaJS的链接
1.官方文档:https://code.angularjs.org/1.5.7/docs/api 2.A Better Way to Learn AngularJS:https://thinkster ...
- 当客户端为RemoteAnywhere时Chef-server 使用knife-windows bootstrap的一个问题
笔者在使用knife-windows bootstrap 一个安装了RemoteAnywhere的节点遇到一个坑: knife bootstrap 192.168.1.245 -r 'role[my_ ...
- 普通用户 crontab 任务不运行
今天发如今linux下,普通用户的crontab任务不运行.网上搜了好多.好多说要在运行的脚本前面加上例如以下内容 if [ -f ~/.bash_profile ]; then . ~/.bas ...
- C语言面向对象编程(五):单链表实现(转)
这里实现的单链表,可以存储任意数据类型,支持增.删.改.查找.插入等基本操作.(本文提供的是完整代码,可能有些长.) 下面是头文件: #ifndef SLIST_H #define SLIST_H # ...
- android-seekbar的thumb图片不居中显示的处理办法
seekbar更换图片后,发现thumb的图片不会居中(竖直方向)显示了,代码如下: <SeekBar android:id="@+id/wb_seekbar" androi ...
- Parallel小记
List<Temp> tList = new List<Temp>(); ; i < ; i++) { tList.Add(new Temp() { id = i, na ...
- Caused by: org.hibernate.boot.registry.selector.spi.StrategySelectionException: Unable to resolve name [org.hibernate.cache.ehcache.EhCacheRegionFactory] as strategy [org.hibernate.cache.spi.RegionFac
警告: Exception encountered during context initialization - cancelling refresh attempt: org.springfram ...
- @using (Html.BeginForm()) @using (Ajax.BeginForm(new AjaxOptions() { })) 区别
@using (Html.BeginForm()) 返回页面 也是页面 都是返回页面 只是 多了一个 data-ajax="true"
