[洛谷P1074] 靶形数独

洛谷题目链接:靶形数独

题目描述

小城和小华都是热爱数学的好学生，最近，他们不约而同地迷上了数独游戏，好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了，于是他们向 Z 博士请教，Z 博士拿出了他最近发明的“靶形数独”，作为这两个孩子比试的题目。




靶形数独的方格同普通数独一样，在 9 格宽×9 格高的大九宫格中有 9 个 3 格宽×3 格高的小九宫格（用粗黑色线隔开的）。在这个大九宫格中，有一些数字是已知的，根据这些数字，利用逻辑推理，在其他的空格上填入 1 到 9 的数字。每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。




但靶形数独有一点和普通数独不同，即每一个方格都有一个分值，而且如同一个靶子一样，离中心越近则分值越高。（如图）

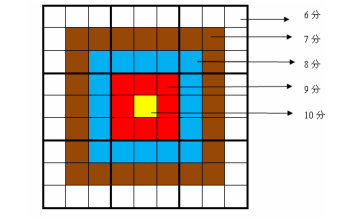
上图具体的分值分布是：最里面一格（黄色区域）为 10 分，黄色区域外面的一圈（红色区域）每个格子为 9 分，再外面一圈（蓝色区域）每个格子为 8 分，蓝色区域外面一圈（棕色区域）每个格子为 7 分，最外面一圈（白色区域）每个格子为 6 分，如上图所示。




比赛的要求是：每个人必须完成一个给定的数独（每个给定数独可能有不同的填法），而且要争取更高的总分数。而这个总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。




如图，在以下的这个已经填完数字的靶形数独游戏中，总分数为 2829。



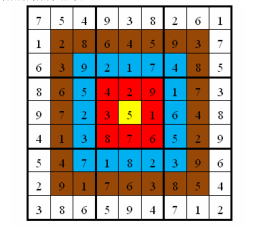
游戏规定，将以总分数的高低决出胜负。




由于求胜心切，小城找到了善于编程的你，让你帮他求出，对于给定的靶形数独，能够得到的最高分数。

输入输出格式

输入格式：

一共 9 行。每行 9 个整数（每个数都在 0―9 的范围内），表示一个尚未填满的数独方

格，未填的空格用“0”表示。每两个数字之间用一个空格隔开。

输出格式：

输出共 1 行。

输出可以得到的靶形数独的最高分数。如果这个数独无解，则输出整数-1。

输入输出样例

输入样例#1：

7 0 0 9 0 0 0 0 1

1 0 0 0 0 5 9 0 0

0 0 0 2 0 0 0 8 0

0 0 5 0 2 0 0 0 3

0 0 0 0 0 0 6 4 8

4 1 3 0 0 0 0 0 0

0 0 7 0 0 2 0 9 0

2 0 1 0 6 0 8 0 4

0 8 0 5 0 4 0 1 2

输出样例#1：

2829

输入样例#2：

0 0 0 7 0 2 4 5 3

9 0 0 0 0 8 0 0 0

7 4 0 0 0 5 0 1 0

1 9 5 0 8 0 0 0 0

0 7 0 0 0 0 0 2 5

0 3 0 5 7 9 1 0 8

0 0 0 6 0 1 0 0 0

0 6 0 9 0 0 0 0 1

0 0 0 0 0 0 0 0 6

输出样例#2：

2852

说明

【数据范围】

40%的数据，数独中非 0 数的个数不少于 30。

80%的数据，数独中非 0 数的个数不少于 26。

100%的数据，数独中非 0 数的个数不少于 24。

NOIP 2009 提高组 第四题

简述一下题意:给出一个未填满的数独,要求出一种情况使得得到的分数最大(得分方式就不多说了,看上面).




首先可以想到的是爆搜求出所有的数独求解情况,然后再验证.

这样可以通过80%的数据.




然后我们可以再想一下如何优化.很显然一个数独局面是不好剪枝的.所以我们可以想一下平时我们是怎么做数独的(没做过就看看吧).

很显然为了求出解,有些数字是已经可以确定了的,然后通过这些确定了的数字再去推出其他可以被确定的数字.




但是我们要怎么样让电脑知道怎么样确定那些数字呢? 其实并不需要确定,只需要使它在搜索的过程中尽量少的回溯,就达到了优化的效果.所以虽然不知道要在那些地方确定数字,但是显然被填入数字多的那一行或那一列能再被填入的数字就少了一些,如果从这些地方开始搜,那么很显然遇到需要回溯的情况就会少很多.

于是优化策略就得到了:每次从已填入数字最多的那一行/列搜.

下面看一下代码:

#include<bits/stdc++.h>
using namespace std;
const int N=10;
const int inf=2147483647;

int a[N][N], ans = -1, use[N];//某个数被使用的次数
int B[N], C[N], tot = 0;//B, C记录行/列中已填入数字个数
bool b[N][N];//某行是否已填入某数
bool c[N][N];//column and number(列)
bool d[N][N];//block and number(某个九宫格)
int sum[N];//the sum of the i_th circle
int mxx, mxy, stc, stl;

void out(){
    for(int i=1;i<=9;i++){
	    for(int j=1;j<=9;j++)
	        printf("%d ",a[i][j]);
	    printf("\n");
    }
    printf("\n");
}

int get(int x,int y){//positions
    return ((y-1)/3)*3+((x-1)/3+1);
}

void qmax(){
    int res = 0;
    memset(sum,0,sizeof(sum));
    for(int i=1;i<=5;i++){
	    for(int j=i;j<=10-i;j++)
	        sum[i] += a[i][j]+a[10-i][j]+a[j][i]+a[j][10-i];
	    sum[i] -= a[i][i]+a[10-i][i]+a[i][10-i]+a[10-i][10-i];
	    res += sum[i] * (i+5);
    }
    res += a[5][5]*10;
    ans = max(ans , res);
}

void dfs(int x,int y,int rest){
    //printf("x=%d y=%d rest=%d\n",x,y,rest);
    mxx = mxy = -inf;
    if(!rest){qmax(); return;}
    for(int i=1;i<=9;i++){
	    int temp = get(x,y);
	    if(use[i] == 0 || b[y][i] || c[x][i] || d[temp][i] || a[y][x]) continue;
	    use[i]--; B[y]++; C[x]++; a[y][x] = i;
	    b[y][i] = c[x][i] = d[temp][i] = 1;
	    for(int j=1;j<=9;j++)
	        if(mxx < B[j] && B[j] < 9)
		        mxx = B[j], stl = j;
	    for(int j=1;j<=9;j++)
	        if(a[stl][j] == 0 && mxy < C[j])
		        mxy = C[j], stc = j;//确定下次搜索填数字的位置,下同
	    dfs(stc , stl , rest-1);
	    use[i]++; B[y]--; C[x]--; a[y][x] = 0;
	    b[y][i] = c[x][i] = d[temp][i] = 0;
    }
}

int main(){
    //freopen("lousy.in","r",stdin);
    //freopen("lousy.out","w",stdout);
    for(int i=1;i<=9;i++) use[i] = 9;
    for(int i=1;i<=9;i++)
	    for(int j=1;j<=9;j++){
	        cin >> a[i][j];
	        if(a[i][j] != 0){
	        b[i][a[i][j]] = 1; B[i]++;
	        c[j][a[i][j]] = 1; C[j]++;
	        d[get(j,i)][a[i][j]] = 1;
	        use[a[i][j]]--; tot++;
        }
    }
    for(int j=1;j<=9;j++)
	    if(mxx < B[j] && B[j] < 9)
	        mxx = B[j], stl = j;
    for(int j=1;j<=9;j++)
	    if(a[stl][j] == 0 && mxy < C[j])
	        mxy = C[j], stc = j;
    dfs(stc,stl,81-tot);
    printf("%d\n",ans);
    return 0;
}