ACM数论之旅7---欧拉函数的证明及代码实现（我会证明都是骗人的╮(￣▽￣)╭）

欧拉函数，用φ(n)表示

欧拉函数是求小于等于n的数中与n互质的数的数目

辣么，怎么求哩？~(～o￣▽￣)～o

可以先在1到n-1中找到与n不互质的数，然后把他们减掉

比如φ(12)

把12质因数分解，12=2*2*3，其实就是得到了2和3两个质因数

然后把2的倍数和3的倍数都删掉

2的倍数：2,4,6,8,10,12

3的倍数：3,6,9,12

本来想直接用12 - 12/2 - 12/3

但是6和12重复减了

所以还要把即是2的倍数又是3的倍数的数加回来 (＞﹏＜)

所以这样写12 - 12/2 - 12/3 + 12/(2*3)

这叫什么，这叫容斥啊，容斥定理听过吧

比如φ(30)，30 = 2*3*5

所以φ(30) = 30 - 30/2 - 30/3 - 30/5 + 30/(2*3) + 30/(2*5) + 30/(3*5) - 30/(2*3*5)

但是容斥写起来好麻烦(￣.￣)

有一种简单的方法

φ(12)   =   12*(1 - 1/2)*(1 - 1/3)                 =   12*(1 - 1/2 - 1/3 + 1/6)

φ(30)   =   30*(1 - 1/2)*(1 - 1/3)*(1 - 1/5)   =   30*(1 - 1/2 - 1/3 - 1/5 + 1/6 + 1/10 + 1/15 - 1/30)

你看( •̀∀•́ )，拆开后发现它帮你自动帮你容斥好

所以φ(30)的计算方法就是先找30的质因数

分别是2,3,5

然后用30* 1/2 * 2/3 * 4/5就搞定了

顺便一提，phi(1) = 1

代码如下：

 //欧拉函数
 int phi(int x){
     int ans = x;
     for(int i = ; i*i <= x; i++){
         if(x % i == ){
             ans = ans / i * (i-);
             while(x % i == ) x /= i;
         }
     }
     if(x > ) ans = ans / x * (x-);
     return ans;
 }

（phi就是φ的读音）

机智的代码，机智的我(｡・`ω´･)

这个的复杂度是O（√n），如果要你求n个数的欧拉函数，复杂度是O（n√n），这也太慢了

有更快的方法

跟埃筛素数差不多

 #include<cstdio>
 const int N =  + ;
 int phi[N];
 void Euler(){
     phi[] = ;
     for(int i = ; i < N; i ++){
         if(!phi[i]){
             for(int j = i; j < N; j += i){
                 if(!phi[j]) phi[j] = j;
                 phi[j] = phi[j] / i * (i-);
             }
         }
     }
 }
 int main(){
     Euler();
 }

（Euler就是欧拉）

另一种，比上面更快的方法

需要用到如下性质

p为质数

1. phi(p)=p-1   因为质数p除了1以外的因数只有p，故1至p的整数只有p与p不互质

2. 如果i mod p = 0, 那么 phi(i * p)=phi(i) * p         （我不会证明）

3.若i mod p ≠0,  那么 phi( i * p )=phi(i) * ( p-1 )   （我不会证明）

（所以我说我会证明都是骗人的╮(￣▽￣)╭）

代码如下：

 #include<cstdio>
 using namespace std;
 const int N = 1e6+ ;
 int phi[N], prime[N];
 int tot;//tot计数，表示prime[N]中有多少质数
 void Euler(){
     phi[] = ;
     for(int i = ; i < N; i ++){
         if(!phi[i]){
             phi[i] = i-;
             prime[tot ++] = i;
         }
         for(int j = ; j < tot && 1ll*i*prime[j] < N; j ++){
             if(i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j]-);
             else{
                 phi[i * prime[j] ] = phi[i] * prime[j];
                 break;
             }
         }
     }
 }
 
 int main(){
     Euler();
 }

最后说下

a^b % p  不等价  (a%p)^(b%p) % p

因为

a^φ(p) ≡ 1 (mod p)

所以

a^b % p  =  (a%p)^(b%φ(p)) % p

（欧拉函数前提是a和p互质）

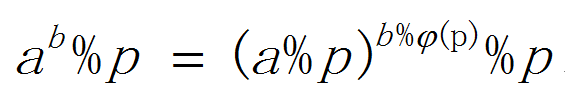
如果p是质数

直接用这个公式

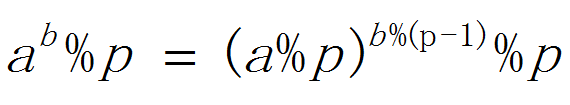
机智的代码，机智的我(｡・`ω´･)

///////////////////////////////////////////////

2016年7月23号

我的天哪，我又发现了一个新公式，貌似可以摆脱a和p互质的束缚，让我们来命名为：超欧拉取模进化公式

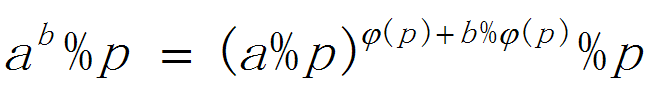
这是历史性的一刻，妈妈再也不用为a和p不互质而担心了= =