拉格朗日乘法与KKT条件

问题的引出

给定一个函数$f$，以及一堆约束函数$g_1,g_2,...,g_m$和$h_1,h_2,...,h_l$.带约束的优化问题可以表示为

\[\min_{X \in R^n}f(X) \quad s.t. \; g_i(X) \leq 0 \; , \;h_j(X) = 0
\]

下面我们将来讨论具有上述问题的解，一共可以分为四种情况：

无约束条件
只有等式约束条件
只有不等式约束条件
同时有等式和不等式约束条件

无约束条件

我们先来复习一下多元函数取得极值的条件。设$f: R^n \to R$,是一个连续可导的函数，并且$J_f$和$H_f$分别是$f$的一阶梯度和二阶梯度矩阵（Hession矩阵）,判断$f(x^*)$是它的一个极值的条件是：

$J_f=0,H_f$是负定矩阵,则$x^*$是$f$的极大值
$J_f=0,H_f$是正定矩阵,则$x^*$是$f$的极小值
$J_f=0,H_f$是半正定或半负定或不定矩阵,则需要进一步讨论

这样，无约束下的最优化问题可以通过上述规则来求函数的极值。

等式约束条件

只含等式约束条件的最优化问题表示为（以一个等式约束为例）

\[\min_{X \in R^n} f(X) \quad s.t. \; h(X) = 0.
\]

下面用具体的实例来讨论这一类问题，令

\[f(X)=x_1+x_2 \quad,\; h(X)=x_1^2+x_2^2-2
\]

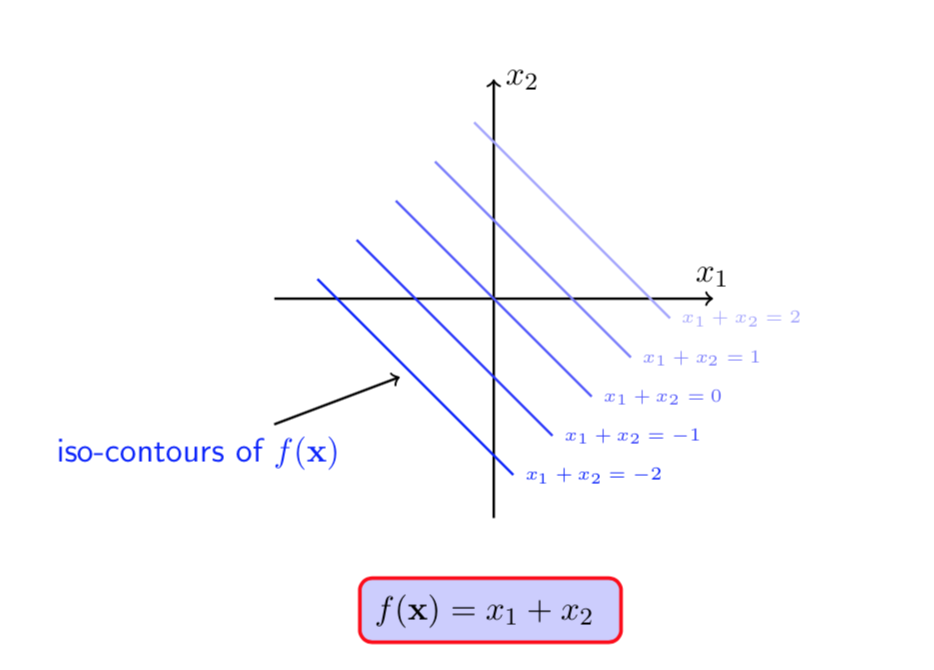
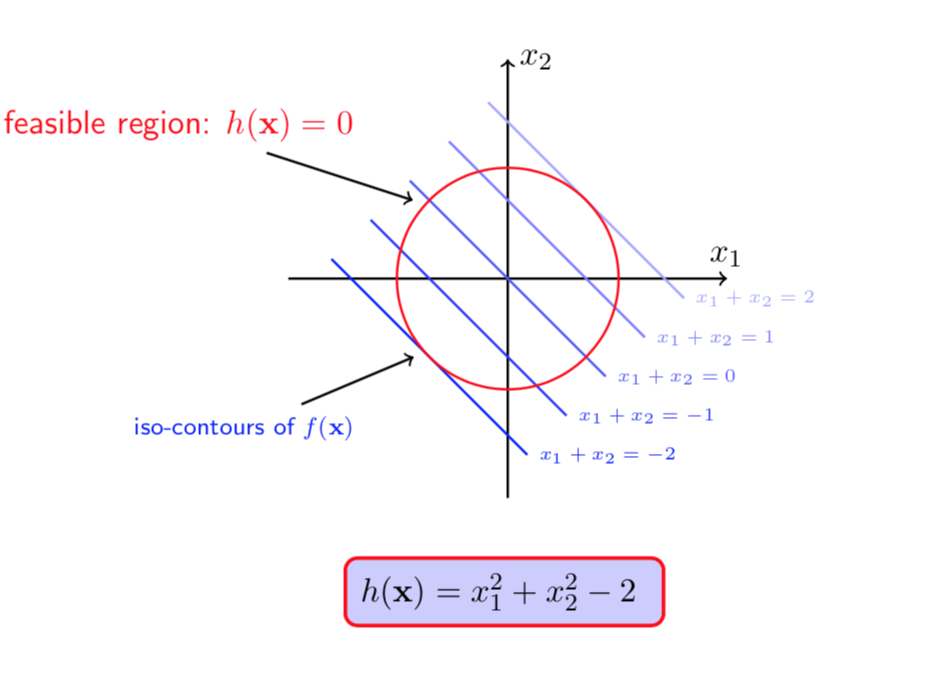
                              图（1 ）                                                        图（2）

在图（1）和（2）中蓝色线是$f(X)$的等高线，红色线是在$h(X) = 0$约束下的可行域（$X$可取值的可行范围）。

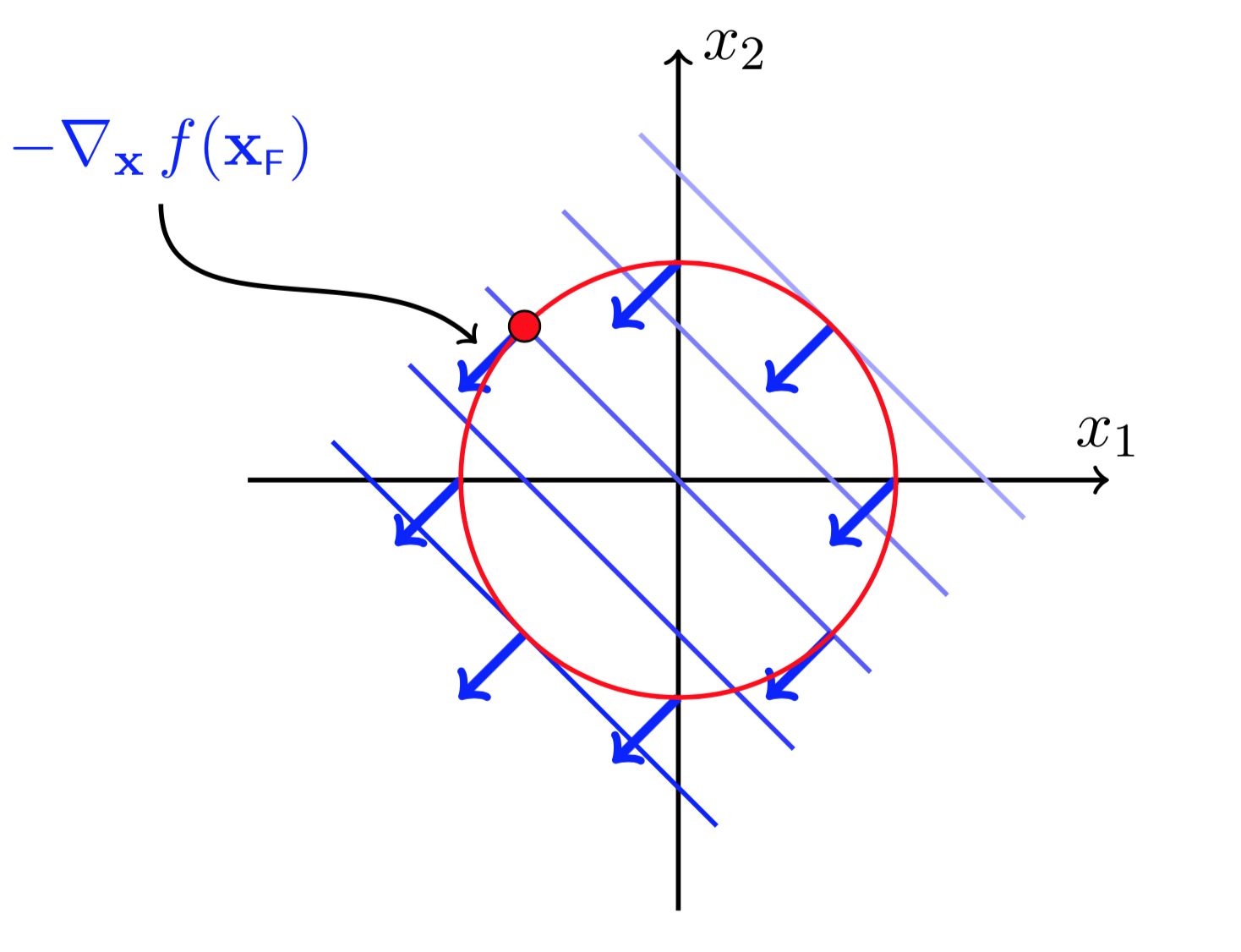
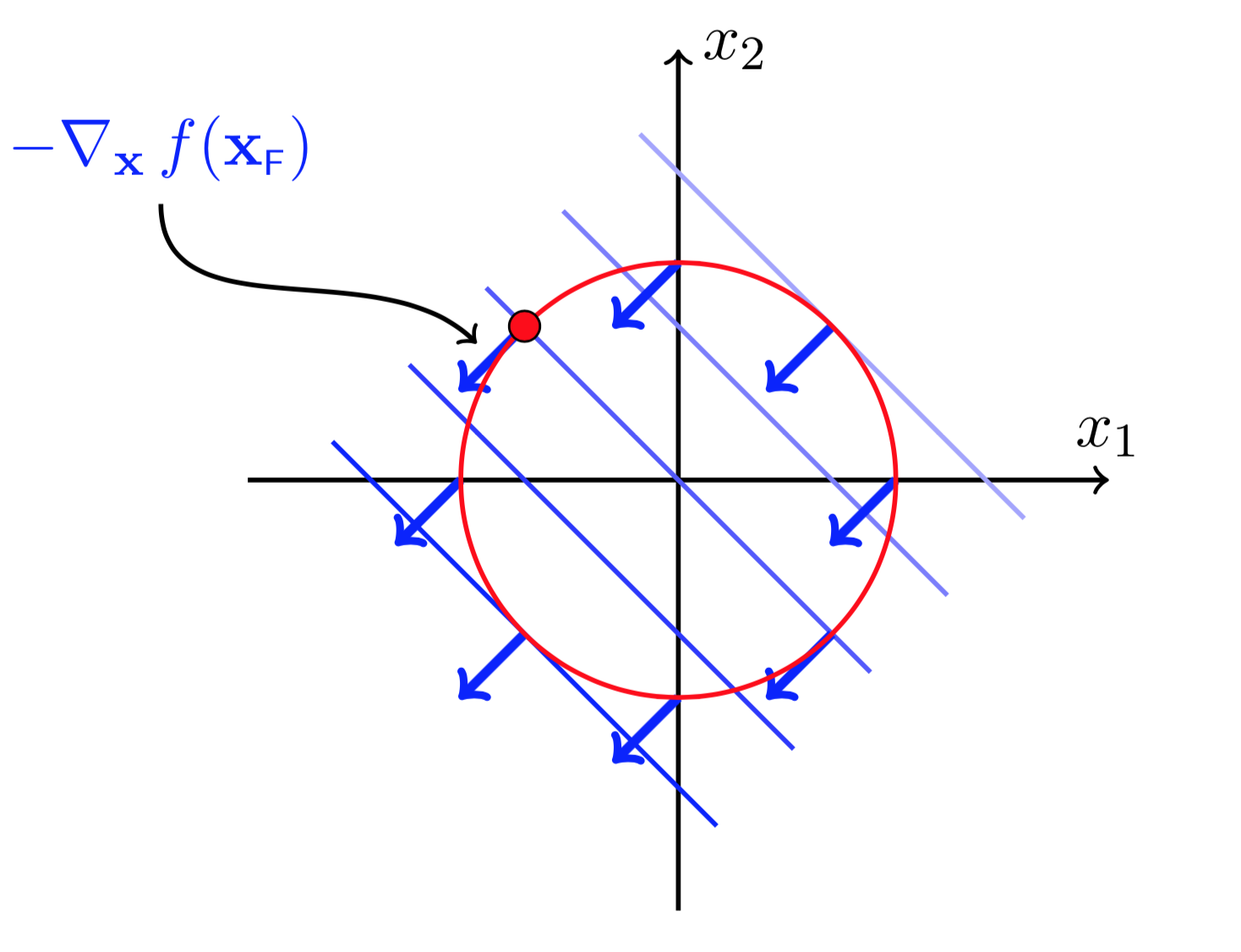
                              图（3 ）                                                        图（4）

为了找到$f(X)$的最小值。如图（3），我们需要从红色点的位置（点$X_F$）往某一个方向走一小步，并且目标位置依然在可行域内(满足$h(X)=0$的限制），同时还希望$f(X)$的值能够下降，即

\[h(X_F + \Delta X) = 0 \quad and \quad f(X_F) >f(X_F+ \Delta X)
\]

我们知道沿着梯度的反方向是下降最快的。如果要满足$\quad f(X_F) >f(X_F+ \Delta X)$则必须有

\[\Delta X \cdot (-\nabla_x f(X)) > 0
\]

意思就是说，下一步走的方向$\Delta X$应该与$-\nabla_Xf(X)$的夹角小于等于90度。

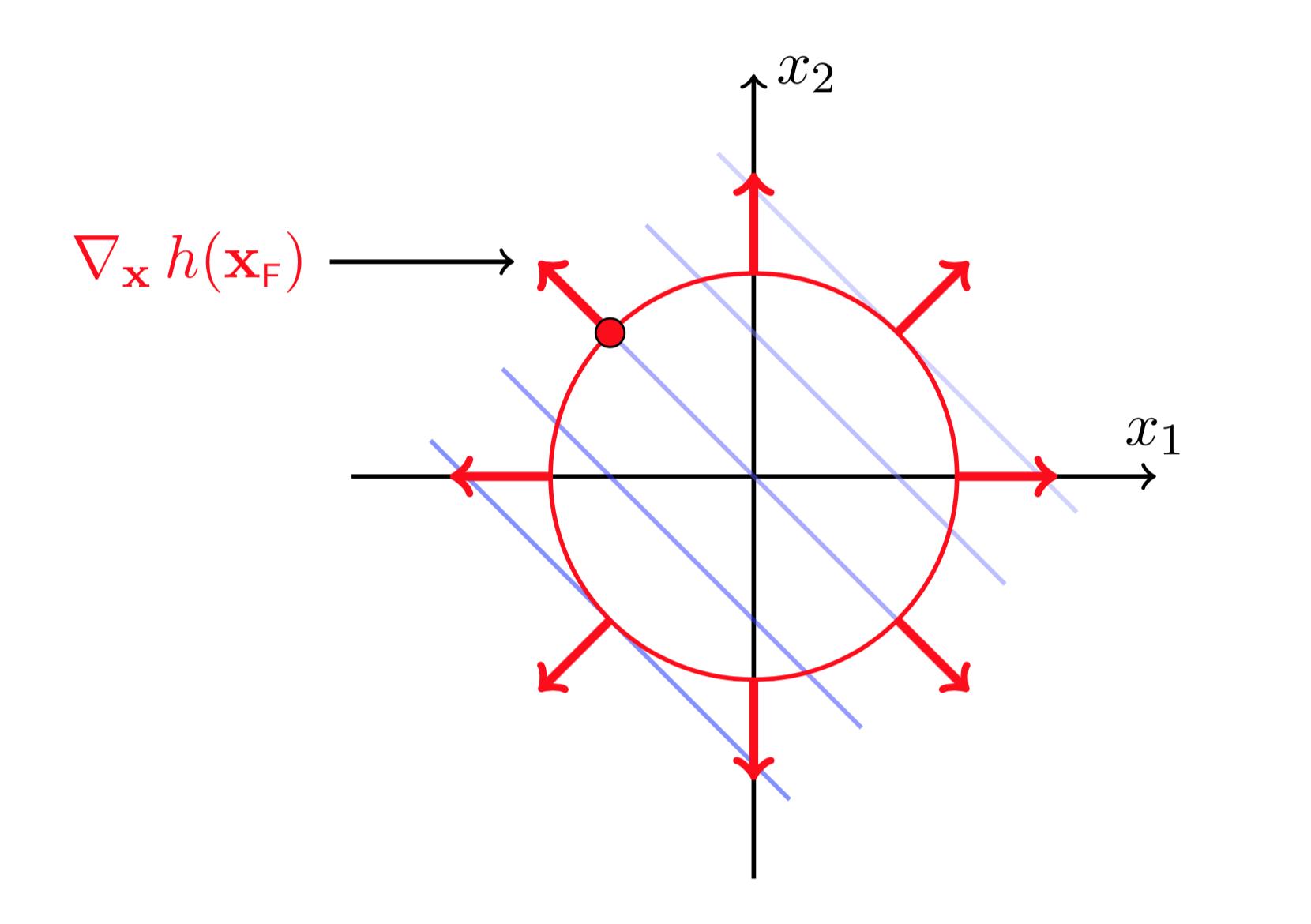
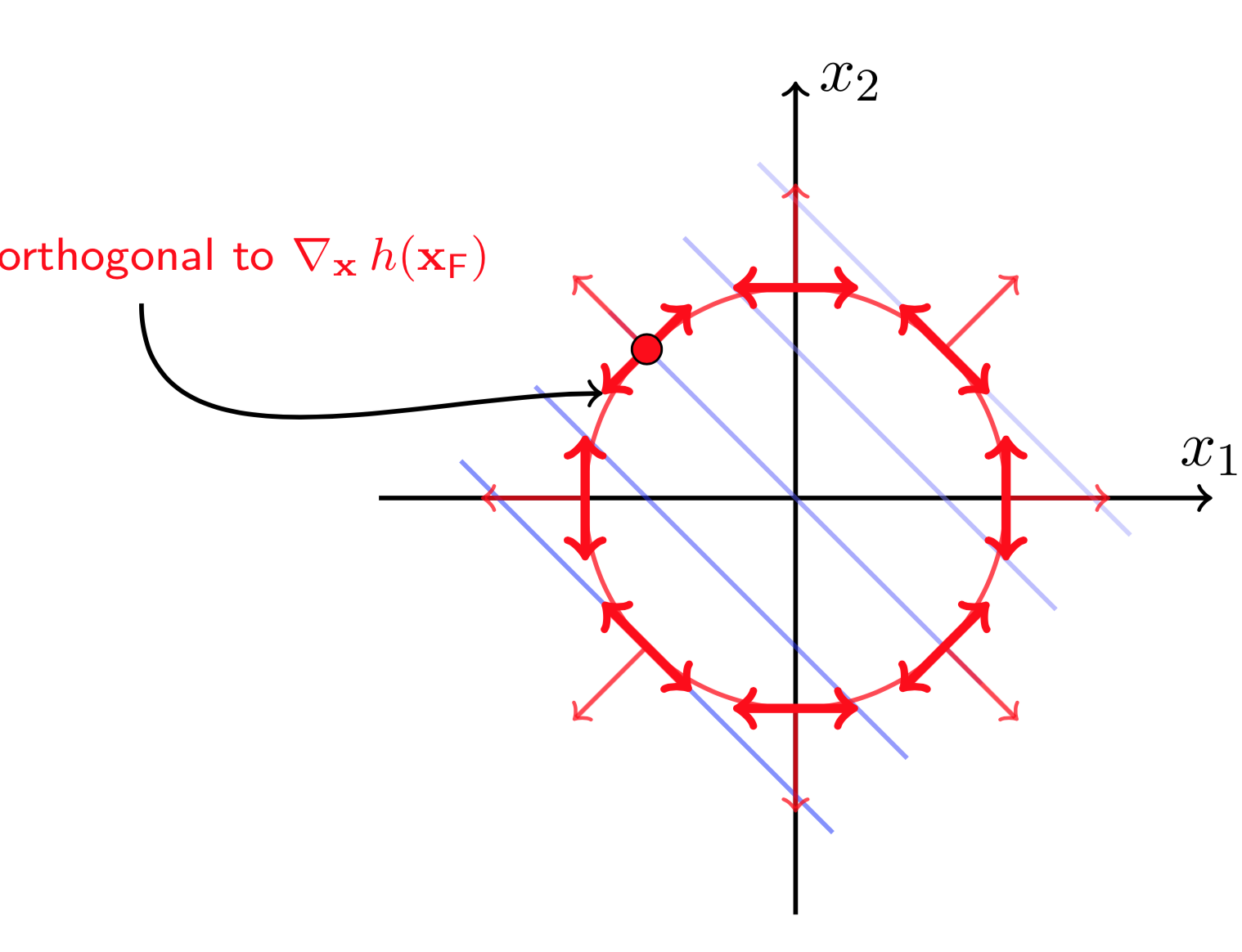
                              图（5 ）                                                        图（6）

图（5）和图（6）分别画出了约束函数$h(X)$的梯度方向以及梯度的正交方向。为了限制在移动$X_F$后，使得$X_F+\Delta X$依然在约束曲线上，则$\Delta X$必须沿着$h(X)$梯度的正交方向移动（否则$h(X)$会增大或减小，这样不再满足约束条件$h(X)= 0$）。这说明任何时刻都有

$\Delta X$沿着$\nabla_Xh(X_F)$正交方向移动，可以保证$h(X_F+\Delta X)=0$.
当$f(X_F) >f(X_F+ \Delta X) $时，必须有

\[\Delta X \cdot (-\nabla_X f(X)) > 0
\]

考虑一种情况

\[\nabla_X f(X_F) = \mu \nabla_X h(X_F)
\]

其中$\mu$是一个常数，此时

当移动$\Delta X$时，$\Delta X \cdot (-\nabla_x f(X)) = -\mu\Delta X \cdot \nabla_x h(X) = 0$.
无法找到一个方向$\Delta X$使得$f(X)$能够继续减小或增大，此时$X_F$是函数的一个极值点.

回到我们最初的问题

\[\min_{X \in R^n} f(X) \quad s.t. \; h(X) = 0.
\]

定义拉格朗日函数

\[L(X,\lambda) = f(X) +\lambda h(X)
\]

$X^*$是一个局部最小值的充分条件是

$\nabla _XL(X^*,\mu^*) = 0$.
$\nabla _{\mu}L(X^*,\mu^*) = 0$.
$Y^T\nabla_{XX}^2L(X^*,\mu^*)Y>0 \quad s.t. \;(\nabla_Xh(X^*))^TY = 0$

最后的约束条件是保证$Y$的方向与$h(X)$梯度方向正交。上面结论很容易推广到多等式约束问题，设

\[\min_{X \in R^n} f(X) \quad s.t. \; h_i(X) = 0 \quad i=1,2,...,l
\]

定义拉格朗日函数

\[L(X,\lambda) = f(X) +\sum_{i=1}^l\mu_i h_i(X) = f(X)+\mu^Th(X)
\]

$X^*$是一个局部最小值的充分条件是

$\nabla _XL(X^*,\mu^*) = 0$.
$\nabla _{\mu}L(X^*,\mu^*) = 0$.
$Y^T\nabla_{XX}^2L(X^*,\mu^*)Y>0 \quad s.t. \;(\nabla_Xh(X))^TY = 0$

不等式约束条件

只包含一个不等式约束的优化问题

\[\min_{X \in R^n} f(X) \quad s.t. \; g(X) \leq 0.
\]

为了便于理解，我们设

\[f(X) =x_1^2+x_2^2, \\
g(X)=x_1^2+x^2_2-1.
\]

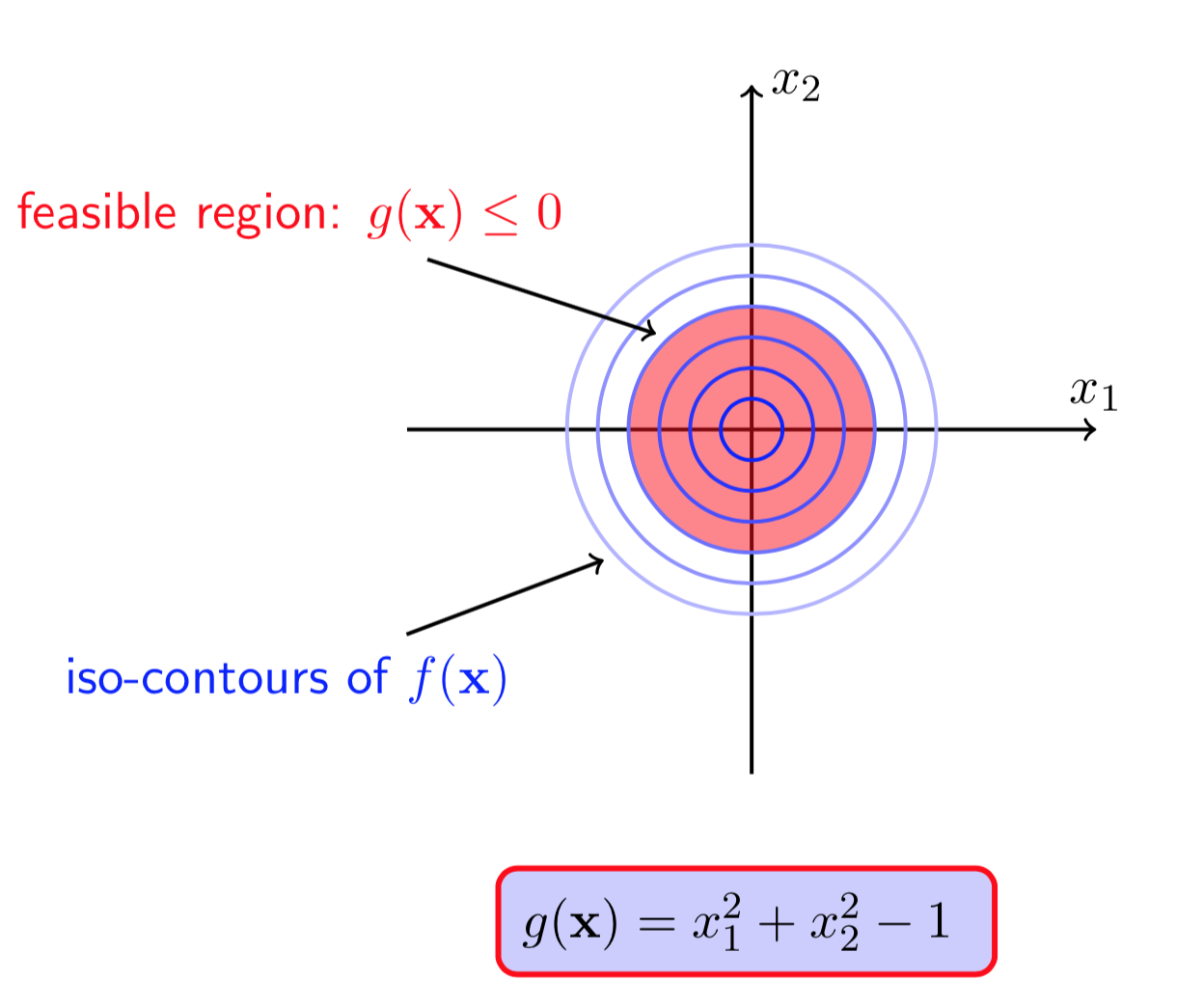
                              图（7 ）                                                        图（8）

图（7）画出了$f(X)$的等高线，并且点$(0,0)$是一个极小值点，图（8）的红色区域是在$g(X)$约束条件下的可行域。从图中可以看出，无论是否有$g(X)$的约束，函数$f(X)$的极小值点都在$(0,0)$处，此时我们称该约束未被激活（$g(X^*)<0$）.现在，如果把目标函数修改成

\[f(X)=(x_1-1.1)^2+(x_2-1.1)^2
\]

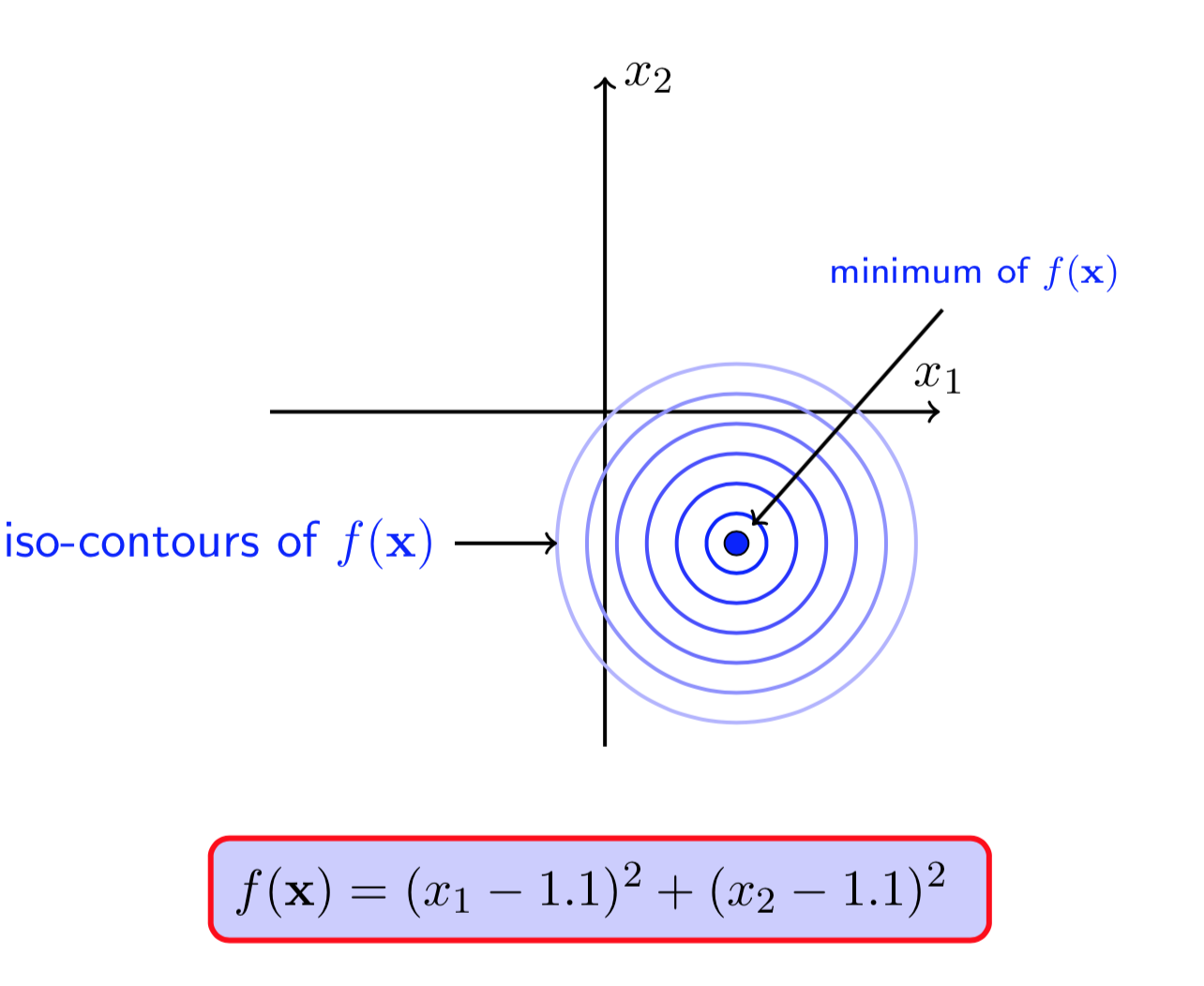
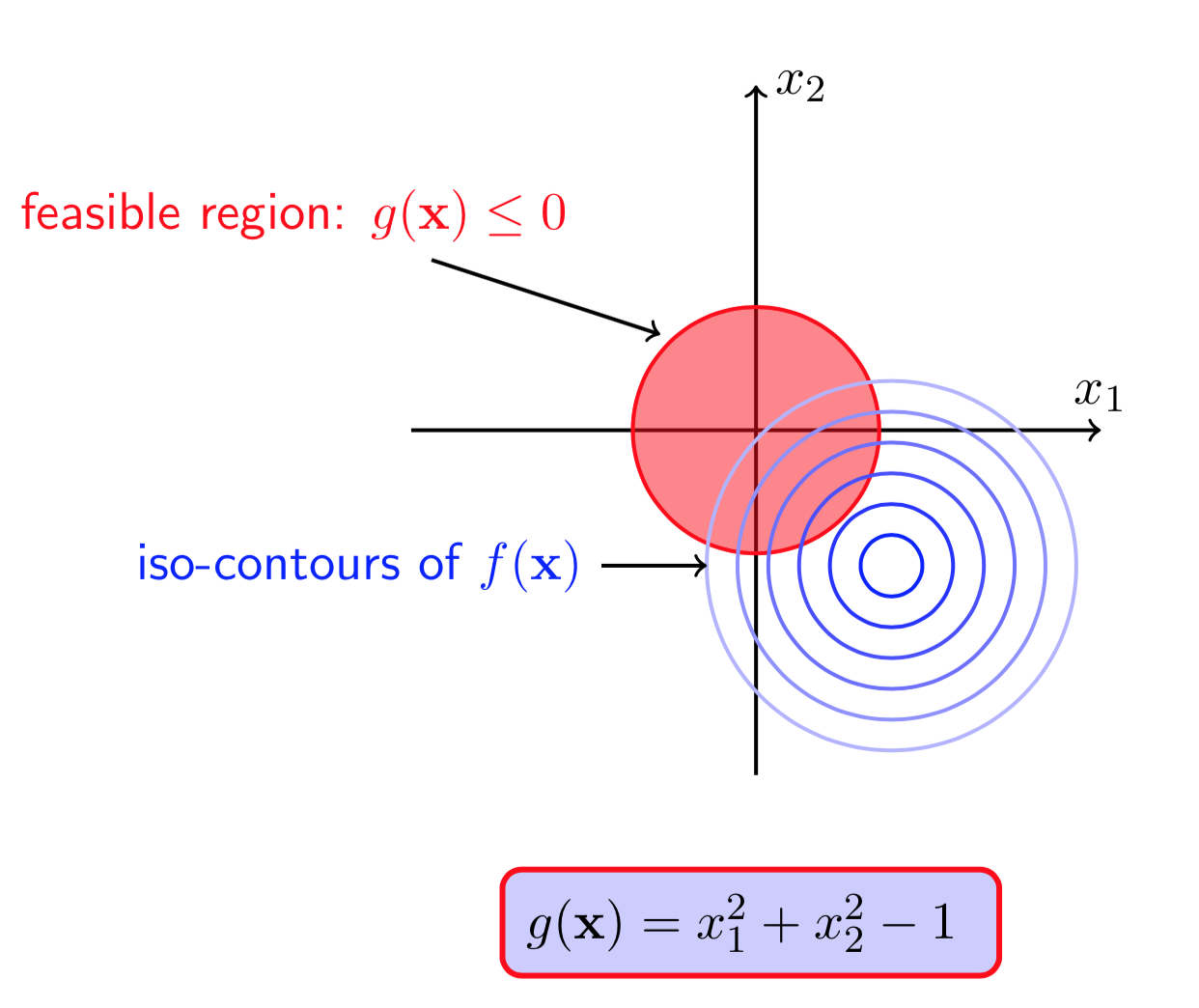
                              图（9 ）                                                        图（10）

图（9）和（10）显示，$f(X)$在无约束条件下的极值点是$(1.1,1.1)$,但是它并不在$g(X)\leq0$的可行域中。这种情况下，若$X^*$是$f(X)$满足约束条件的一个极小值点，那么一定有$g(X^*)=0$,也即极小值点一定在约束的边界上取得。实际上，此处的不等式约束就变成了等式约束。

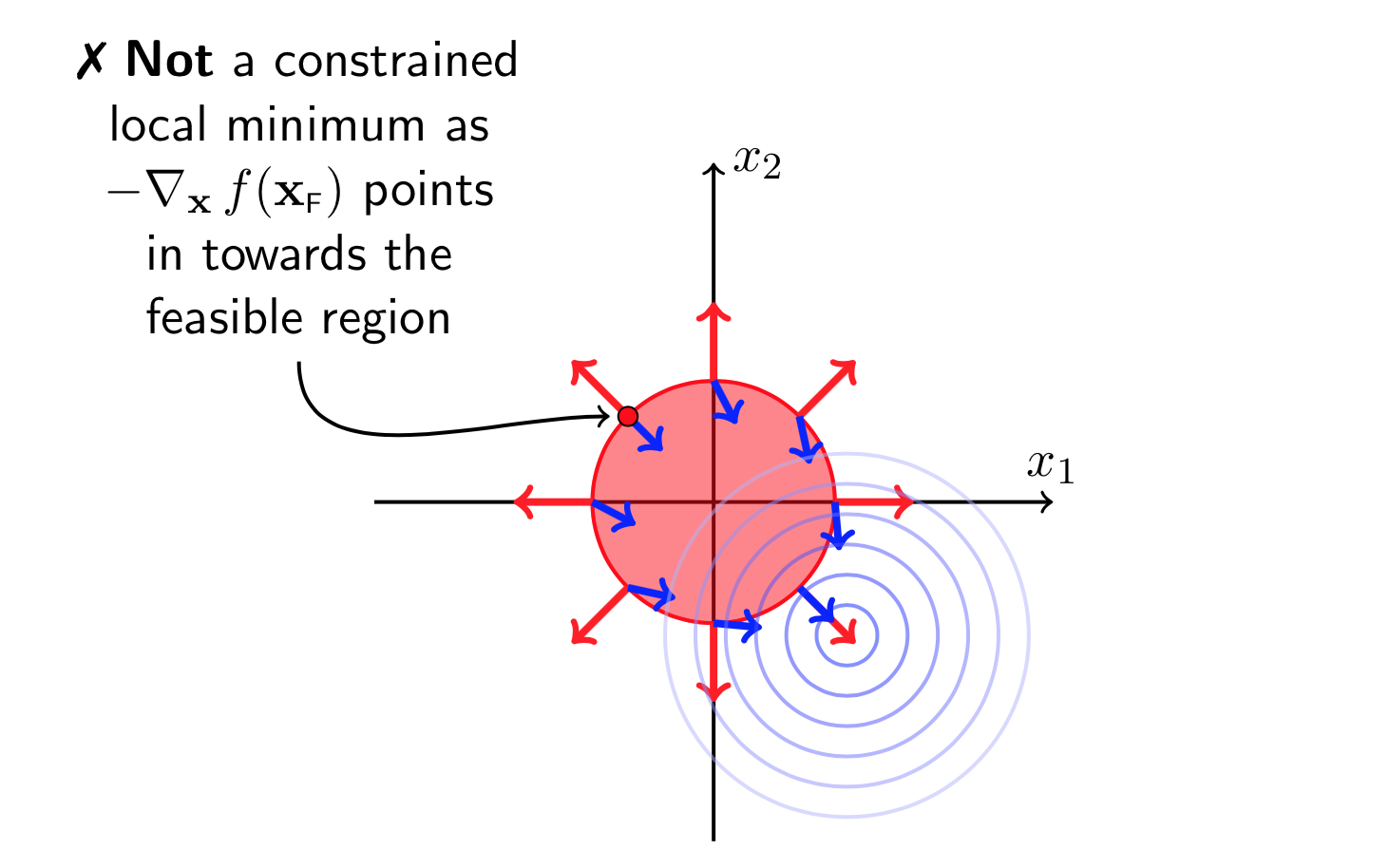
图（11）

从图(11)可以看出来，在极小值点处$-\nabla f(X)$与$\nabla g(X)$的方向是一致的

\[-\nabla f(X) = \lambda \nabla g(X)\quad and \quad \lambda >0
\]

其实这也不难理解,如果说$X^*$是一个极小值点，上面分析知道$g(X)\leq 0$被激活，所以$g(X^*)=0$,如果设从点$X^*$出发下一步可行的方向为$\Delta X$，由于要满足$g(X^*+\Delta X) \leq 0$,所以

\[\Delta X \cdot \nabla g(X^*) \leq 0 \quad (1)
\]

所以下一步的所有可行方向需要满足上述不等式约束，因为$X^*$是一个极小值点，也就是说沿着满足上式(1)的$\Delta X$的方向，都有$f(X^) \leq f(X^+\Delta X) $，也就是

\[\Delta X \cdot \nabla f(X^*) \geq 0 \quad (2)
\]

并且我们知道$X^*$一定在$g(X)=0$上，通过上一节的等式约束的条件，应有

\[\nabla f(X^*) = \mu \nabla g(X^*) \quad (3)
\]

通过$(1,2,3)$式可知$\mu \leq 0$，从而$\lambda = -\mu \geq 0$.

现在我们来总结一下上面讨论的结果，给出优化问题

\[\min_{X \in R^n} f(X) \quad s.t. \; g(X) \leq 0.
\]

如果$X^*$是一个极小值点，则可能有一下两种情况：

Case 1: 无约束条件的极小值点出现在可行域内
- $g(X^*) < 0$.
- $\nabla _X f(X^*) = 0$.
- $\nabla^2 _{XX}f(X)$是一个正定矩阵.
Case 2: 无约束条件的极小值点出现在可行域外
- $g(X^*)=0$.
- $-\nabla _Xf(X^*) = \lambda \nabla g(X^*) \quad where \quad \lambda > 0$.
- $Y^T\nabla_{XX}^2L(X^*)Y \geq 0 \quad s.t. \;(\nabla_Xg(X^*))^TY = 0$

下面，直接引入$KKT$条件

\[\min_{X \in R^n} f(X) \quad s.t. \; g(X) \leq 0.
\]

定义拉格朗日函数

\[L(X,\lambda) = f(X)+\lambda g(X).
\]

$X^*$是一个局部最小值等价于存在唯一的$\lambda^*$满足

KKT1 . $\nabla _X L(X^*,\lambda^*)=0$.
KKT2. $\lambda ^* \geq 0$.
KKT3. $\lambda ^*g(X^*) = 0$.
KKT4. $g(X^*) \leq 0$.
KKT5. 矩阵$\nabla _{XX}L(X^*,\lambda ^*)$正定.

上面就是$KKT$条件。这些条件其实可以分两种情况

Case 1: 约束未激活
- 此时$\lambda ^* = 0,L(X^*,\lambda^*)=f(X^*)$,
- KKT1 $\Rightarrow \nabla _Xf(X^*)=0$.
- KKT4 $\Rightarrow X^*$是一个可行点
Case 2: 约束被激活
- 此时$\lambda ^* \geq 0,L(X^*,\lambda^*)=f(X^*)+\lambda ^*g(X^*)$,
- KKT1 $\Rightarrow \nabla _Xf(X^*) =- \lambda \nabla g(X^*)$.
- KKT3 $\Rightarrow g(X^*) = 0$.并且$L(X^*,\lambda^*)=f(X^*)$.

将问题推广到多个不等式约束

\[\min_{X \in R^n} f(X) \quad s.t. \; g_i(X) \leq 0. \quad i =1,2,...,m
\]

定义拉格朗日函数

\[L(X,\lambda) = f(X) +\sum_{i=1}^m\lambda_i g_i(X) = f(X)+\lambda^Tg(X)
\]

$X^*$是一个局部最小值等价于存在唯一的$\lambda^*$满足

KKT1 . $\nabla _X L(X^*,\lambda^*)=0$.
KKT2. $\lambda _j^* \geq 0\quad j=1,2...,m$.
KKT3. $\lambda_j^*g_j(X^*) = 0 \quad j=1,2,...,m$.
KKT4. $g_j(X^*) \leq 0 \quad j=1,2,...,m$.
KKT5. 矩阵$\nabla _{XX}L(X^*,\lambda ^*)$正定.

同时存在等式和不等式约束

我们回到最开始的情况，同时存在多个等式约束和多个不等式约束

\[\min_{X \in R^n}f(X) \quad s.t. \; g_i(X) \leq 0 \; , \;h_j(X) = 0 \quad, i =1,2,...,l \quad and \quad j =1,2,...,m
\]

定义拉格朗日函数

\[L(X,\lambda) = f(X) +\sum_{j=1}^l\mu_j h_j(X)+\sum_{i=1}^m\lambda_i g_i(X) = f(X)+\mu^Th(X) +\lambda^Tg(X)
\]

$X^*$是一个局部最小值等价于存在唯一的$\lambda^*$满足

KKT1 . $\nabla _X L(X^*,\mu^*,\lambda^*)=0$.
KKT2. $\lambda _j^* \geq 0\quad j=1,2,...,m$.
KKT3. $\lambda_j^*g_j(X^*) = 0 \quad j=1,2,...,m$.
KKT4. $g_j(X^*) \leq 0 \quad j=1,2,...,m$.
KKT5. $h_i(X^*) = 0 \quad i =1,2,...,l$
KKT6. 矩阵$\nabla _{XX}L(X^*,\lambda ^*)$正定.

下面通过一个例子来加深理解，考虑问题

\[\min \quad x_1^2+x_2^2 \\
s.t. \quad x_1+x_2 = 1. \\
x_2 \leq \alpha .
\]

构造拉格朗日函数

\[L(x_1,x_2,\lambda, \mu) = x_1^2+x_2^2+\mu(x_1+x_2-1)+\lambda(x_2-\alpha)
\]

KKT方程如下：

\[\nabla _xL=(2x_1+\mu,2x_2+\mu+\lambda) = 0,\\
x_1+x_2 = 1, \quad \quad\quad\quad\quad\quad\quad\quad\quad\\
x_2 \leq \alpha, \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\
\lambda \geq 0, \quad\quad\quad\quad\quad\quad\quad\quad \quad\quad\quad\;\;\\
\lambda(x_2-\alpha) =0.\quad\quad\quad\quad\quad \quad\quad\quad
\]

联立得

\[\lambda \geq 2 - 4 \alpha
\]

当$\alpha \ge 1/2$时，$\lambda = 0 \geq 2 -4 \alpha$,此时约束条件未被激活，原问题的最优解为$(x_1,x_2)=(1/2,1/2)$.
当$\alpha < 1/2$时，$\lambda = 2 - 4\alpha > 0$，从而$x_2-\alpha = 0$,即$x_2=\alpha$,此时约束条件被激活，愿问题最优解为$(x_1,x_2)=(1-\alpha,\alpha)$.