Codeforces Round #454 (Div. 1) CodeForces 906D Power Tower (欧拉降幂)

题目链接：http://codeforces.com/contest/906/problem/D

题目大意：给定n个整数w[1],w[2]，……,w[n]，和一个数m，然后有q个询问，每个询问给出一个l,r,求w[l]^w[l+1]^w[l+2]……w[r]  %m  ,即a[l]到a[r]的幂次方

解题思路：利用欧拉降幂公式

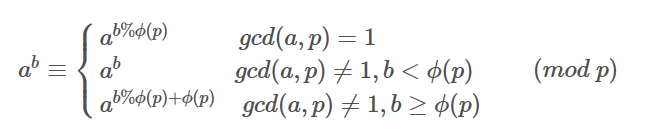
第一个要求a和p互质，第2个和第3个为广义欧拉降幂，不要求a和p互质，用在这题刚好。

因为有两种情况，所以我们需要自定义一下降幂取模公式。

我们对整个区间进行递归处理，每一个数的指数是它后一个数到右端点的幂。

递归终止条件为到右端点或者p的欧拉函数值为1,再求欧拉函数值的时候我们需要进行记忆化，否则会超时

代码：

#include<iostream>
#include<cstdio>
#include<map>
using namespace std;
#define ll long long
#define MOD(a,b) a>=b?a%b+b:a
#define N 100005
map<ll,ll> mp;
int n,l,r,q;
ll mod,w[N];
ll qpow(ll a,ll b,ll p){
    ll res=;
    while(b){
        if(b&) res=MOD(res*a,p); //为保证指数结果正确，应该用自定义取模
        b>>=;
        a=MOD(a*a,p);
    }
    return res;
}
ll phi(ll x){
    if(mp[x]) return mp[x];
    ll tmp=x,res=x;
    for(int i=;i*i<=x;i++){
        if(x%i==){
            res=res*(i-)/i;
            while(x%i==) x/=i;
        }
    }
    if(x>) res=res*(x-)/x;
    return mp[tmp]=res;
}
ll solve(int l,int r,ll m){
    if(l==r||m==) return MOD(w[l],m);
    else return qpow(w[l],solve(l+,r,phi(m)),m);
}
int main() {
    scanf("%d%I64d",&n,&mod);
    for(int i=;i<=n;i++) scanf("%I64d",&w[i]);
    scanf("%d",&q);
    while(q--){
        scanf("%d%d",&l,&r);
        printf("%I64d\n",solve(l,r,mod)%mod);
    }
    return ;
}

bzoj 3884 上帝与集合的正确用法

题目链接：https://www.lydsy.com/JudgeOnline/problem.php?id=3884

题目大意：和上题很像，只不过所有数都是2，且次方是无穷的了，给定一个正整数p，求2^(2^(2^(2^(2^...)))) mod p的值

解题思路：方法几乎是一样的，因为每次递归幂的模数就会变成原来的欧拉函数值，所以最多经过log（p），模数就会变成1，然后后面结果都一样的了，没必要递归下去，直接结束就好了。

代码：

#include<iostream>
#include<cstdio>
#include<map>
using namespace std;
#define ll long long
#define MOD(a,b) a>=b?a%b+b:a
#define N 100005
map<ll,ll> mp;
int n,l,r,q;
ll mod;
ll qpow(ll a,ll b,ll p){
    ll res=;
    while(b){
        if(b&) res=MOD(res*a,p);
        b>>=;
        a=MOD(a*a,p);
    }
    return res;
}
ll phi(ll x){
    if(mp[x]) return mp[x];
    ll tmp=x,res=x;
    for(int i=;i*i<=x;i++){
        if(x%i==){
            res=res*(i-)/i;
            while(x%i==) x/=i;
        }
    }
    if(x>) res=res*(x-)/x;
    return mp[tmp]=res;
}
ll solve(ll m){
    if(m==) return ;
    else return qpow(,solve(phi(m)),m);
}
int main() {
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%lld",&mod);
        printf("%lld\n",solve(mod)%mod);
    }
    return ;
}