Riverside Curio

Riverside Curio

time limit per test1 second

memory limit per test256 megabytes

Arkady decides to observe a river for n consecutive days. The river's water level on each day is equal to some real value.

Arkady goes to the riverside each day and makes a mark on the side of the channel at the height of the water level, but if it coincides with a mark made before, no new mark is created. The water does not wash the marks away. Arkady writes down the number of marks strictly above the water level each day, on the i-th day this value is equal to mi.

Define di as the number of marks strictly under the water level on the i-th day. You are to find out the minimum possible sum of di over all days. There are no marks on the channel before the first day.

Input

The first line contains a single positive integer n (1 ≤ n ≤ 105) — the number of days.

The second line contains n space-separated integers m1, m2, ..., mn (0 ≤ mi < i) — the number of marks strictly above the water on each day.

Output

Output one single integer — the minimum possible sum of the number of marks strictly below the water level among all days.

Examples

input

6

0 1 0 3 0 2

output

6

input

5

0 1 2 1 2

output

1

input

5

0 1 1 2 2

output

0

Note

In the first example, the following figure shows an optimal case.

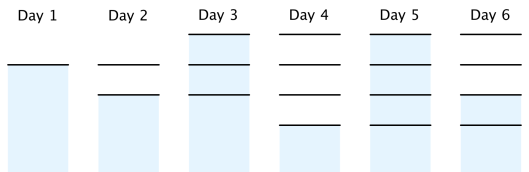
Note that on day 3, a new mark should be created because if not, there cannot be 3 marks above water on day 4. The total number of marks underwater is 0 + 0 + 2 + 0 + 3 + 1 = 6.

In the second example, the following figure shows an optimal case.

这道题很妙啊~~~

我们可以假设\(t[i]\)表示第\(i\)天所有的水位线条数，显然\(t[i] = d[i] + 1 + m[i]\)

由于题目要求的是\(min(\sum d[i])\)，我们就可以转化为求\(min(\sum t[i])\)

接下来我们来看看\(t\)这个数列应该满足什么条件：

\(t_i ≥ max(t_{i-1}, m_i + 1)\)

\(t_i ≥ t_{i+1}-1\)

由第二个条件可以推出\(t_i ≥ t_j-(j-i)\ \ (j>i)\)

那么我们来想一件事，是不是有一个合法的数列\(t\)，就一定有一种对应的合法方案吗？

条件一看出，任意两个相邻的数的差小于等于1.（当然，后面的大于等于前面的）

显然，如果\(t[i]\)是递增的，那么没有任何问题。

如果有两个相邻的数相等时，说明新画的水位线和以前的一条重合了。

那么我们来思考一个问题，什么时候会产生矛盾。

当你发现你后面需要\(x\)根水位线，但是你当前的方案一共都没有这么多条的时候就矛盾了。

那么会不会出现这种情况呢？

这种情况是\(m[i] > t[i-1]\)的时候，由于\(t_i ≥ max(t_{i-1}, m_i + 1)\)，所以\(t_i ≥ m_i+1\)

又因为相邻两个数的差不超过1，所以\(t_i ≥ t_{i-1}\)，所以这种情况不存在。

简单的证明完毕。

接下来考虑代码实现问题：

我们要构造这个数列，也就是要满足上述条件。

那么我们可以这样构造

先让所有的数都等于\(m_i + 1\)，然后遍历一遍

发现\(t_{i-1}>t_i, t_i = t_{i-1}\)

这样就满足条件一了。

紧接着去满足条件二，我们可以倒着遍历一遍，如果发现不满足条件的，就强行变成满足条件的最优解。

#include<bits/stdc++.h>
long long m[200000],t[200000],ans,n;
int main()
{
	scanf("%I64d",&n);
	for (int i=1;i<=n;++i) scanf("%I64d",&m[i]),t[i]=m[i]+1;
	for (int i=2;i<=n;++i) if (t[i]<t[i-1]) t[i]=t[i-1];
	for (int i=n;i>=2;--i) if (t[i-1]<t[i]-1) t[i-1]=t[i]-1;
	for (int i=1;i<=n;++i) ans+=t[i]-1-m[i];
	printf("%I64d",ans);
	return 0;
}