Python数据结构与算法？

数据结构与算法（Python）

冒泡排序

冒泡排序（英语：Bubble Sort）是一种简单的排序算法。它重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

冒泡排序算法的运作如下：

• 比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

冒泡排序的分析

交换过程图示(第一次)：

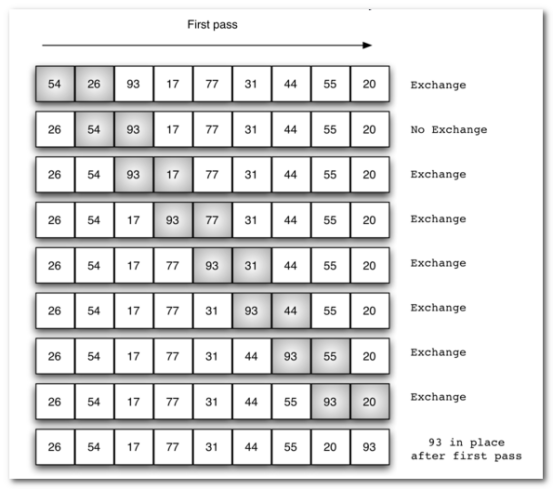
那么我们需要进行n-1次冒泡过程，每次对应的比较次数如下图所示：

 def bubble_sort(alist):

     for j in range(len(alist)-1,0,-1):

         # j表示每次遍历需要比较的次数，是逐渐减小的

         for i in range(j):

             if alist[i] > alist[i+1]:

                 alist[i], alist[i+1] = alist[i+1], alist[i]

 li = [54,26,93,17,77,31,44,55,20]

 bubble_sort(li)

 print(li)

时间复杂度

• 最优时间复杂度：O(n) （表示遍历一次发现没有任何可以交换的元素，排序结束。）
• 最坏时间复杂度：O(n2)
• 稳定性：稳定

冒泡排序的演示

效果：

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

选择排序分析

排序过程：

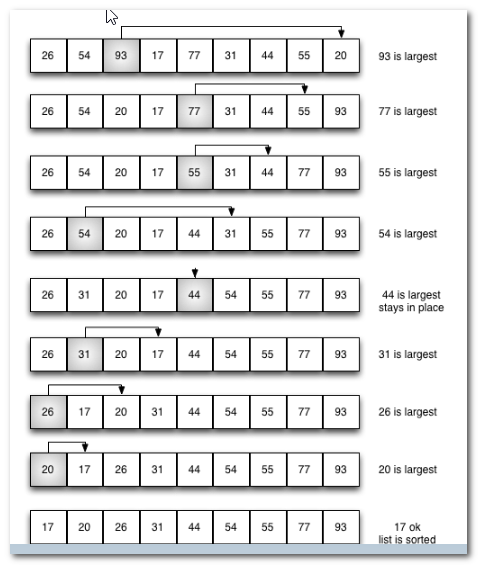
红色表示当前最小值，黄色表示已排序序列，蓝色表示当前位置。

 def selection_sort(alist):

     n = len(alist)

     # 需要进行n-1次选择操作

     for i in range(n-1):

         # 记录最小位置

         min_index = i

         # 从i+1位置到末尾选择出最小数据

         for j in range(i+1, n):

             if alist[j] < alist[min_index]:

                 min_index = j

         # 如果选择出的数据不在正确位置，进行交换

         if min_index != i:

             alist[i], alist[min_index] = alist[min_index], alist[i]

 alist = [54,226,93,17,77,31,44,55,20]

 selection_sort(alist)

 print(alist)

时间复杂度

• 最优时间复杂度：O(n2)
• 最坏时间复杂度：O(n2)
• 稳定性：不稳定（考虑升序每次选择最大的情况）

选择排序演示

插入排序

插入排序（英语：Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

插入排序分析

 def insert_sort(alist):

     # 从第二个位置，即下标为1的元素开始向前插入

     for i in range(1, len(alist)):

         # 从第i个元素开始向前比较，如果小于前一个元素，交换位置

         for j in range(i, 0, -1):

             if alist[j] < alist[j-1]:

                 alist[j], alist[j-1] = alist[j-1], alist[j]

 alist = [54,26,93,17,77,31,44,55,20]

 insert_sort(alist)

 print(alist)

时间复杂度

• 最优时间复杂度：O(n) （升序排列，序列已经处于升序状态）
• 最坏时间复杂度：O(n2)
• 稳定性：稳定

插入排序演示

快速排序

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

步骤为：

1. 从数列中挑出一个元素，称为"基准"（pivot），
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

快速排序的分析

 复制代码
 def quick_sort(alist, start, end):

     """快速排序"""

     # 递归的退出条件

     if start >= end:

         return

     # 设定起始元素为要寻找位置的基准元素

     mid = alist[start]

     # low为序列左边的由左向右移动的游标

     low = start

     # high为序列右边的由右向左移动的游标

     high = end

     while low < high:

         # 如果low与high未重合，high指向的元素不比基准元素小，则high向左移动

         while low < high and alist[high] >= mid:

             high -= 1

         # 将high指向的元素放到low的位置上

         alist[low] = alist[high]

         # 如果low与high未重合，low指向的元素比基准元素小，则low向右移动

         while low < high and alist[low] < mid:

             low += 1

         # 将low指向的元素放到high的位置上

         alist[high] = alist[low]

     # 退出循环后，low与high重合，此时所指位置为基准元素的正确位置

     # 将基准元素放到该位置

     alist[low] = mid

     # 对基准元素左边的子序列进行快速排序

     quick_sort(alist, start, low-1)

     # 对基准元素右边的子序列进行快速排序

     quick_sort(alist, low+1, end)

 alist = [54,26,93,17,77,31,44,55,20]

 quick_sort(alist,0,len(alist)-1)

 print(alist)
 复制代码

时间复杂度

• 最优时间复杂度：O(nlogn)
• 最坏时间复杂度：O(n2)
• 稳定性：不稳定

从一开始快速排序平均需要花费O(n log n)时间的描述并不明显。但是不难观察到的是分区运算，数组的元素都会在每次循环中走访过一次，使用O(n)的时间。在使用结合（concatenation）的版本中，这项运算也是O(n)。

在最好的情况，每次我们运行一次分区，我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此，在到达大小为一的数列前，我们只要作log n次嵌套的调用。这个意思就是调用树的深度是O(log n)。但是在同一层次结构的两个程序调用中，不会处理到原来数列的相同部分；因此，程序调用的每一层次结构总共全部仅需要O(n)的时间（每个调用有某些共同的额外耗费，但是因为在每一层次结构仅仅只有O(n)个调用，这些被归纳在O(n)系数中）。结果是这个算法仅需使用O(n log n)时间。

快速排序演示

希尔排序

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

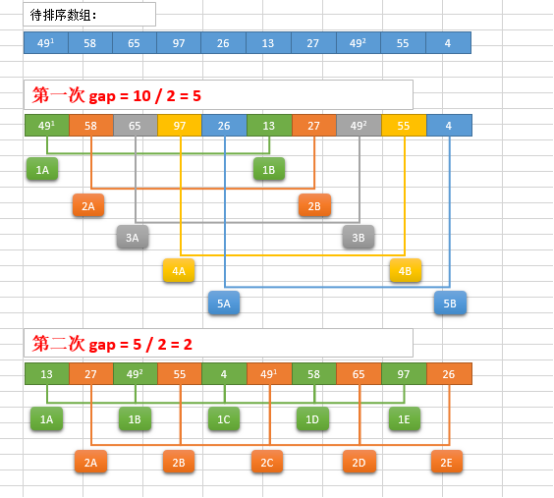
希尔排序过程

希尔排序的基本思想是：将数组列在一个表中并对列分别进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身还是使用数组进行排序。

例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样(竖着的元素是步长组成)：

最后以1步长进行排序（此时就是简单的插入排序了）

希尔排序的分析

 def shell_sort(alist):

     n = len(alist)

     # 初始步长

     gap = n / 2

     while gap > 0:

         # 按步长进行插入排序

         for i in range(gap, n):

             j = i

             # 插入排序

             while j>=gap and alist[j-gap] > alist[j]:

                 alist[j-gap], alist[j] = alist[j], alist[j-gap]

                 j -= gap

         # 得到新的步长

         gap = gap / 2

 alist = [54,26,93,17,77,31,44,55,20]

 shell_sort(alist)

 print(alist)

时间复杂度

• 最优时间复杂度：根据步长序列的不同而不同
• 最坏时间复杂度：O(n2)
• 稳定想：不稳定

希尔排序演示

归并排序

归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

将数组分解最小之后，然后合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

归并排序的分析

 def merge_sort(alist):

     if len(alist) <= 1:

         return alist

     # 二分分解

     num = len(alist)/2

     left = merge_sort(alist[:num])

     right = merge_sort(alist[num:])

     # 合并

     return merge(left,right)

 def merge(left, right):

     '''合并操作，将两个有序数组left[]和right[]合并成一个大的有序数组'''

     #left与right的下标指针

     l, r = 0, 0

     result = []

     while l<len(left) and r<len(right):

         if left[l] < right[r]:

             result.append(left[l])

             l += 1

         else:

             result.append(right[r])

             r += 1

     result += left[l:]

     result += right[r:]

     return result

 alist = [54,26,93,17,77,31,44,55,20]

 sorted_alist = mergeSort(alist)

 print(sorted_alist)

时间复杂度

• 最优时间复杂度：O(nlogn)
• 最坏时间复杂度：O(nlogn)
• 稳定性：稳定

搜索

搜索是在一个项目集合中找到一个特定项目的算法过程。搜索通常的答案是真的或假的，因为该项目是否存在。 搜索的几种常见方法：顺序查找、二分法查找、二叉树查找、哈希查找

二分法查找

二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

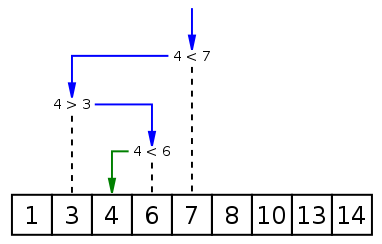
二分法查找实现

（非递归实现）

 def binary_search(alist, item):

       first = 0

       last = len(alist)-1

       while first<=last:

           midpoint = (first + last)/2

           if alist[midpoint] == item:

               return True

           elif item < alist[midpoint]:

               last = midpoint-1

           else:

               first = midpoint+1

     return False

 testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]

 print(binary_search(testlist, 3))

 print(binary_search(testlist, 13))

 （递归实现）
 def binary_search(alist, item):

     if len(alist) == 0:

         return False

     else:

         midpoint = len(alist)//2

         if alist[midpoint]==item:

           return True

         else:

           if item<alist[midpoint]:

             return binary_search(alist[:midpoint],item)

           else:

             return binary_search(alist[midpoint+1:],item)

 testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]

 print(binary_search(testlist, 3))

 print(binary_search(testlist, 13))

时间复杂度

• 最优时间复杂度：O(1)
• 最坏时间复杂度：O(logn)

• 比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。