[洛谷P3938]:斐波那契(fibonacci)（数学）

题目传送门

---

题目描述

小$C$养了一些很可爱的兔子。
有一天，小$C$突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行繁衍：一对兔子从出生后第二个月起，每个月刚开始的时候都会产下一对小兔子。我们假定，在整个过程中兔子不会出现任何意外。
小$C$把兔子按出生顺序，把兔子们从$1$开始标号，并且小$C$的兔子都是$1$号兔子和$1$号兔子的后代。如果某两对兔子是同时出生的，那么小$C$会将父母标号更小的一对优先标号。
如果我们把这种关系用图画下来，前六个月大概就是这样的：

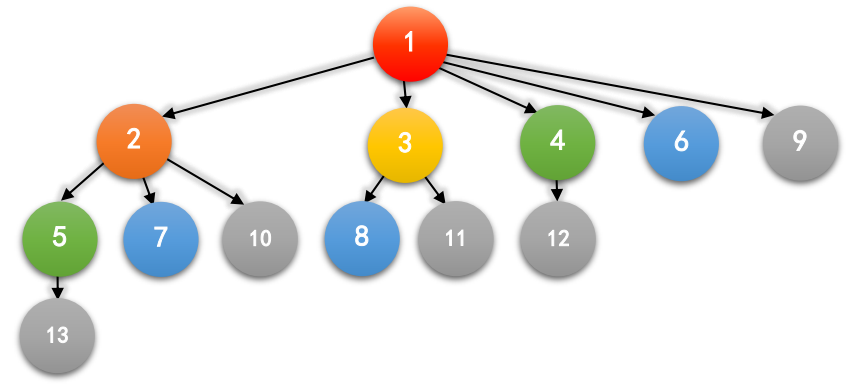
其中，一个箭头$A\rightarrow B$表示$A$是$B$的祖先，相同的颜色表示同一个月出生的兔子。
为了更细致地了解兔子们是如何繁衍的，小$C$找来了一些兔子，并且向你提出了$m$个问题：她想知道关于每两对兔子$a_i$和$b_i$，他们的最近公共祖先是谁。你能帮帮小$C$吗？

一对兔子的祖先是这对兔子以及他们父母（如果有的话）的祖先，而最近公共祖先是指两对兔子所共有的祖先中，离他们的距离之和最近的一对兔子。比如，$5$和$7$的最近公共祖先是$2$，$1$和$2$的最近公共祖先是$1$，$6$和$6$的最近公共祖先是$6$。

---

输入格式

输入第一行，包含一个正整数$m$。
输入接下来$m$行，每行包含$2$个正整数，表示$a_i$和$b_i$。

---

输出格式

输入一共$m$行，每行一个正整数，依次表示你对问题的答案。

---

样例

样例输入1：

5
1 1
2 3
5 7
7 13
4 12

样例输出1：

1
1
2
2
4

样例输入2：

10
13 5
13 6
13 7
13 8
13 9
13 10
13 11
13 12
13 13
13 14

样例输出2：

5
1
2
1
1
2
1
1
13
1

---

数据范围与提示

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表：
测试点     $m$                      $a_i,b_i$           特殊性质$1$           特殊性质$2$
  $1$          $\leqslant 11$                  $\leqslant 15$                  $\surd$                         $\surd$
  $2$          $\leqslant 12$                  $\leqslant 15$                  $\times$                         $\times$
  $3$          $\leqslant 13$                  $\leqslant 1000$             $\surd$                         $\times$
  $4$          $\leqslant 14$                  $\leqslant 1000$             $\times$                         $\times$
  $5$          $\leqslant 1005$             $\leqslant{10}^6$                $\surd$                        $\times$
  $6$          $\leqslant 1006$             $\leqslant{10}^6$                $\times$                        $\surd$
  $7$          $\leqslant 1007$             $\leqslant{10}^6$                $\times$                        $\times$
  $8$          $\leqslant 300008$        $\leqslant{10}^{12}$              $\surd$                        $\times$
  $9$          $\leqslant 300009$        $\leqslant{10}^{12}$              $\times$                        $\surd$
  $10$        $\leqslant 300010$        $\leqslant{10}^{12}$              $\times$                        $\times$

特殊性质$1$：保证$a_i,b_i$均为某一个月出生的兔子中标号最大的一对兔子。例如，对于前六个月，标号最大的兔子分别是$1,2,3,5,8,13$。
特殊性质$2$：保证$|a_i,b_i|\leqslant 1$。

---

题解

考场上$20$分钟切掉这道题，我感觉还是蛮爽的。

$20\%$算法：

直接手动打表，注意$14$是$1$的儿子，而$15$则是$2$的儿子，挺费眼睛的，而且一开始我打了一个表还没打对……

时间复杂度：$\Theta(m)$。

期望得分：$20$分。

$40\%$算法：

直接暴力建树，每次询问都暴力把这棵树重新建一遍来找父亲。

我觉得写这种方法的就是$\times \times \times$，不用管他……

时间复杂度：$\Theta(m\times {|a|}^2\times \log|a|)$（$|a|$表示$a_i,b_i$的值域）。

期望得分：$40$分。

$60\%$算法：

考虑$QJ$两个特殊情况：

特殊情况$1$：

　　某一个月出生的标号最大的兔子就是斐波那契数列中的一项，画一张图，如下：

　　

　　我们便会惊喜的发现如果这两只兔子同是斐波那契数列的奇数项或偶数项，那么它们的最近公共祖先就是他们当中较小的那个；否则，它们的最近公共祖先为$1$。

特殊情况$2$：

　　如果两只兔子的标号的绝对值等于$1$，则他们的最近公共祖先一定为$1$。

$70\%$算法：

可能细心的你会发现，一个节点一定小于自己儿子的一半，所以我们可以暴力网上找，最多有$\log i$层。

时间复杂度：$\Theta(n+m\log n)$。

期望得分：$70$分。

$100\%$算法：

在考场上，我惊喜的发现了一个规律，一个节点的减去比它小的那个斐波那契数就是他的父亲节点，所以我们可以每次让两个点中更小的那个暴力往上抬，直到相同为止即可。

时间复杂度：$\Theta(60\times m)$。

期望得分：$100$分。

---

代码时刻

$20\%$算法：

#include<bits/stdc++.h>
using namespace std;
int Map[16][16]={
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
0,1,2,1,1,2,1,2,1,1,2,1,1,2,1,2,
0,1,1,3,1,1,1,1,3,1,1,3,1,1,1,1,
0,1,1,1,4,1,1,1,1,1,1,1,4,1,1,1,
0,1,2,1,1,5,1,2,1,1,2,1,1,5,1,2,
0,1,1,1,1,1,6,1,1,1,1,1,1,1,1,1,
0,1,2,1,1,2,1,7,1,1,2,1,1,2,1,2,
0,1,1,3,1,1,1,1,8,1,1,3,1,1,1,1,
0,1,1,1,1,1,1,1,1,9,1,1,1,1,1,1,
0,1,2,1,1,2,1,2,1,1,10,1,1,2,1,2,
0,1,1,3,1,1,1,1,3,1,1,11,1,1,1,1,
0,1,1,1,4,1,1,1,1,1,1,1,12,1,1,1,
0,1,2,1,1,5,1,2,1,1,2,1,1,13,1,2,
0,1,1,1,1,1,1,1,1,1,1,1,1,1,14,1,
0,1,2,1,1,2,1,2,1,1,2,1,1,2,1,15};
int main()
{
	int m;
	scanf("%d",&m);
	while(m--)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		printf("%d\n",Map[a][b]);
	}
	return 0;
}

$60\%$算法：

#include<bits/stdc++.h>
using namespace std;
int m;
long long fi[60];
int getnum(long long x)
{
	int res;
	for(int i=1;i<=59;i++)if(fi[i]==x){res=i;break;}
	return res;
}
int main()
{
	scanf("%d",&m);
	fi[0]=fi[1]=1;
	for(int i=2;i<=59;i++)
		fi[i]=fi[i-1]+fi[i-2];
	for(int i=1;i<=m;i++)
	{
		long long a,b;
		scanf("%lld%lld",&a,&b);
		if(a==b){printf("%lld\n",a);continue;}
		if(a-b==1||b-a==1){puts("1");continue;}
		int numa=getnum(a),numb=getnum(b);
		if(numa!=-1&&numb!=-1&&(numa&1)==(numb&1))printf("%lld\n",min(a,b));
		else puts("1");
	}
	return 0;
}

$70\%$算法：

#include<bits/stdc++.h>
using namespace std;
int m;
struct rec
{
	int nxt;
	int to;
}e[1000001];
int head[1000001],cnt;
int t[1000001],tot=1,tmp,depth[1000001],fa[1000001][23];
bool flag;
void add(int st,int to)
{
	e[++cnt].to=to;
	e[cnt].nxt=head[st];
	head[st]=cnt;
}
void build()
{
	t[1]=1;
	for(int x=1;x<30;x++)
	{
		tmp=tot;
		for(int i=1;i<=tot;i++)
		{
			t[i]++;
			if(t[i]>1)add(i,++tmp);
			if(tmp>=1000000)return;
		}
		tot=tmp;
	}
}
void dfs(int x)
{
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(depth[e[i].to])continue;
		depth[e[i].to]=depth[x]+1;
		fa[e[i].to][0]=x;
		for(int j=1;j<=21;j++)
			fa[e[i].to][j]=fa[fa[e[i].to][j-1]][j-1];
		dfs(e[i].to);
	}
}
int LCA(int x,int y)
{
    if(depth[x]>depth[y])swap(x,y);
    for(int i=21;i>=0;i--)
        if(depth[fa[y][i]]>=depth[x])y=fa[y][i];
    if(x==y)return x;
    for(int i=21;i>=0;i--)
        if(fa[x][i]!=fa[y][i])
        {
            x=fa[x][i];
            y=fa[y][i];
        }
    return fa[x][0];
}
int main()
{
	scanf("%d",&m);
	build();
	depth[1]=1;
	dfs(1);
	while(m--)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		printf("%d\n",LCA(a,b));
	}
	return 0;
}

$100\%$算法：

#include<bits/stdc++.h>
using namespace std;
int m;
long long fi[61];
long long LCA(long long x,long long y)
{
	while(1)
	{
		if(x==y)return x;
		if(x>y){for(int i=1;i<=65;i++)if(fi[i]<x&&fi[i+1]>=x){x-=fi[i];break;}}
		else for(int i=1;i<=65;i++)if(fi[i]<y&&fi[i+1]>=y){y-=fi[i];break;}
	}
}
int main()
{
	fi[1]=fi[2]=1;
	for(int i=3;i<=60;i++)
		fi[i]=fi[i-1]+fi[i-2];
	scanf("%d",&m);
	while(m--)
	{
		long long a,b;
		scanf("%lld%lld",&a,&b);
		printf("%lld\n",LCA(a,b));
	}
	return 0;
}
 

---

rp++